1．さよなら磁界結合

　変成とは一次側から二次側へ交流電圧を変換する機能である．この機能を果たすには二つの導体巻線（コイル）を近傍配置し，その間の相互誘導作用を利用すればよい．理想的にはコイルの巻数比が変成比となる．この仕組みをトランスと呼んでいる．トランス式変成器が活躍する場面として商用電源：50/60Hz，直流直流コンバータ：キロヘルツ帯，ワイヤレス電力伝送：メガヘルツ帯などがある．

　変成の応用範囲を更に広げるにはどうすればよいだろうか．そのきっかけを得るためにトランス式以外の可能性を模索したい．それがこの記事の動機である．磁界結合による相互誘導に頼らずして変成機能を実現することを狙う．果たしてそんな手段は存在するのだろうか．

2．必要機能の本質

　そもそも変成とは本質的にどのような機能なのか考える．磁界結合トランスの先入観を排除し，基本に立ち戻って電圧や電流の振舞いを見つめる．電力の入口と出口を備える受動回路を図1に示すような「箱」で表す．この箱が理想変成器（以下，単に変成器と書く）であるための条件は

である．変成比は正の定数とする．のとき降圧，のとき昇圧となる．を整数や有理数に限定する必然性はない．巻数とかの概念はもう忘れよう．

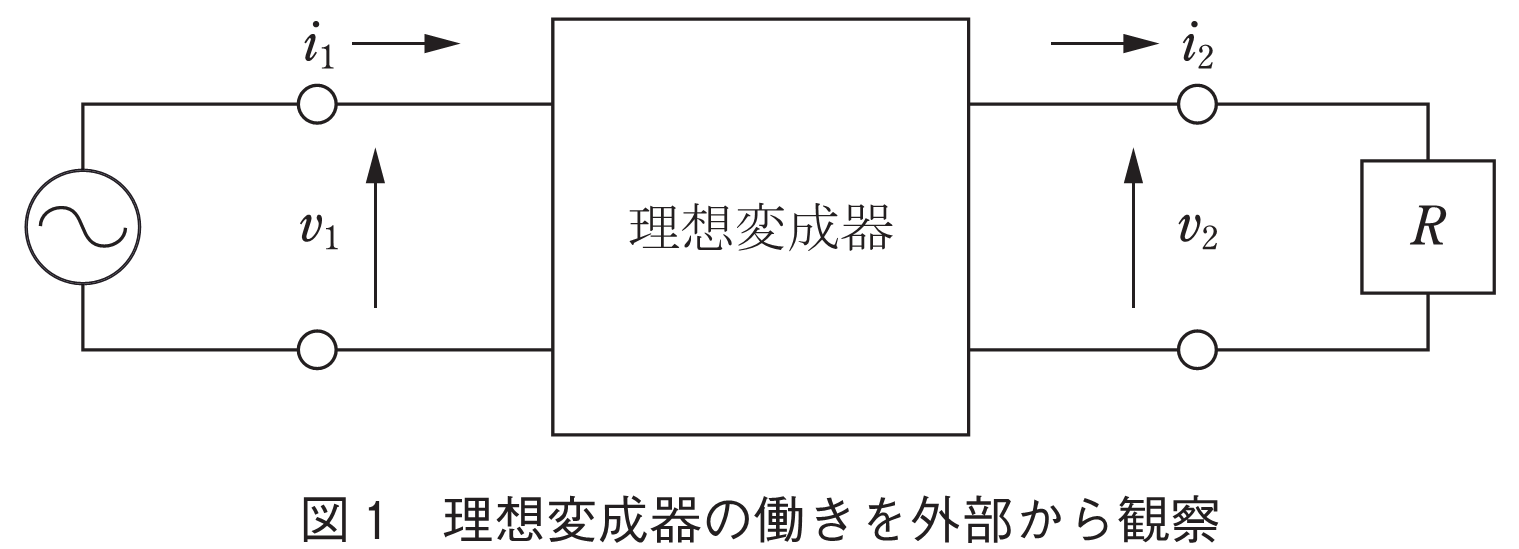
　回路の二次側に負荷抵抗を接続し，式(１)から電圧電流の積と商を計算すると

となる．式(２)は一次側から二次側への電力保存則，つまり箱内で電力が減衰しないことを意味する．これを満たすには

「箱の中にある素子が全て無損失」

(４)

が必要である．もう一つの条件である式(３)はこの箱を回路として見たときの入力イミタンスが負荷抵抗値に正比例することを意味している．すなわちこの箱が変成器であるためには

「式(３)が任意のについて成立」

　(５)

が必要である．

3．キャルキット

　条件(５)中の「任意のについて」はある意味とても厳しい．なぜなら負荷になる可能性のある全てのを箱の出口に順次接続してその都度式(３)が成立するかどうかチェックするのが大変な作業になるからである．