2.1　系統的な符号の構成方法

　Shannonは，入力制約の例としてモールス信号を考えている⁽¹⁾．モールス信号では，2種類の「スペース」，1記号分のスペースとその2倍の長さのスペースがある．一つのスペースが二つ連続すると2倍の長さのスペースと区別がつかなくなるので，これらのスペースは連続してはならない，という制約がある．モールス信号の記号列は，どのようなデータを符号化したとしても，符号化された系列（送信される系列）がこの制約を満たすように作られている．

　ここでは，制約として制約を考える．ある記号が回連続するとき，のように書き，これを「の連」と呼ぶ．を文字の有限集合（有限アルファベット）としたとき，は，の要素から成る有限長の全ての系列（空系列も含む）の集合とする．

［定義1］を非負整数，を非負整数若しくはとし，であるとする．系列に含まれる記号とその次のの間にあるの連の長さが必ず以上であり，に含まれるの連長は全て以下であるとき，は制約を満たすと言う．この制約は図1のようなラベル付き有限有向グラフ（有限オートマトン）で表現できる．

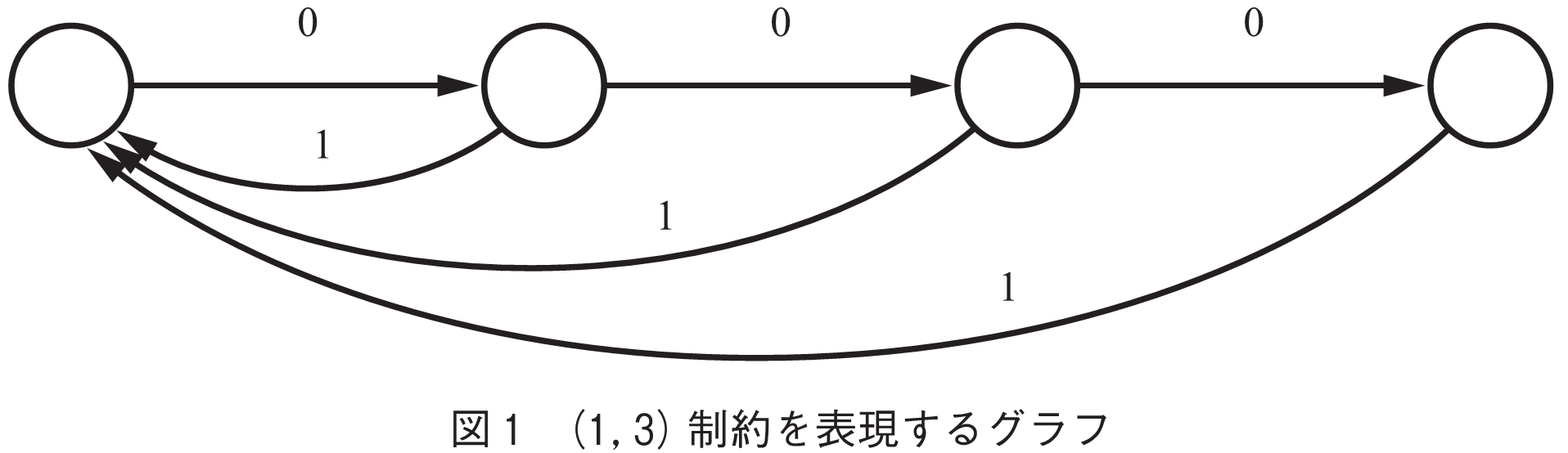
　ある制約を満たすような系列しか入力できない，若しくは伝送できない通信路を入力制約を持つ通信路という．

　磁気記録装置は，記録するデータを入力と考え読出し信号を出力と考えると，一種の通信路とみなすことができる．ハードディスクが長手記録方式（磁化方向がディスク回転する方向と同じ方式．現在のハードディスクは垂直記録方式を採用している．）を採用していたときには，磁気記録通信路は，入力制約として制約を持っていると考えることができた．制約と制約の物理的な意味は次のとおりである．

制約：高い記録密度を達成するために，物理的な1bitを記録するための領域は狭くなっていった．しかし，一つの磁化反転によって出てくるパルス状の信号の時間的な幅は変化しないので，その幅が物理的な1bitの幅よりも相対的に長くなっていった．隣接する磁化反転はその極性が逆なので，これにより一つの磁化反転が隣接する領域に干渉することになり，結果的に出力レベルが下がることになる．このような記号間干渉の発生を防ぐために，磁化反転の間隔がある程度以上長くなることが要請されていた．

制約：データを再生するときには，クロック（記号周波数）を正確に再生することが重要である．この周波数が不正確であれば，ビットが抜けたり，意味のないビットが挿入されたりする．磁気記録では，磁化反転がないと再生信号のレベルは一定になってしまう．したがって，ハードディスクでは，データを記録している部分でも，クロックに関する情報が取り出せるように，ある程度の間隔（電子回路が同期を外さない程度の間隔）で磁化反転が生じるようにという要請があった．物理的な記録方式は異なるが，CDやDVDでも同様の要請がある．

　さて，データは一般には任意の系列であるので，入力制約を満たしているとは限らない．したがって，入力制約を持つ通信路を介してデータを伝送するときには，まずデータを，入力制約を満たす系列に変換しなければならない．また，受信側若しくは再生時には変換された系列から，若干の誤りが含まれているなどの現実的な仮定の下で元のデータ系列をほぼ正確に復号できなければならない．（通常のシステムでは，この復号を行った後で誤り訂正符号の復号を行う．）

　このような変換を行う符号の符号化率はより小さくなければならないが，では，どこまで大きくできるだろうか．それは，次に定義する制約の容量によって定まる．

［定義2］制約の容量制約に対してを以下のように定義し，これをの容量と呼ぶ．

ここで，は，制約を満たす長さがの系列の数である．

　が有限オートマトンで表現できるのであれば，この値は

で与えられる．ここでは，オートマトンを表現する有限有向グラフの遷移行列の最大固有値である．

　Shannonは以下の定理を証明している⁽¹⁾．

［定理3］であれば，符号化率が以下であるような，制約のための符号を構成できる．また，のための符号があれば，その符号化率は以下でなければならない．

　この事実はがと近似できることに対応する．ところで，の定義とこの定理の証明に従って，符号化率がに近い符号を，表引き，若しくは論理回路で構成しようとすると，一般には符号長をかなり長くしなければならない．符号長が長くなると表も論理回路も非常に大きくなる上に，制約によっては収束の速度が非常に遅いこともある（例えば，以下のバランス制約を参照）．したがって，定理の証明の方法をそのまま実際の通信路に応用することは多くの場合に困難である．

　IBMワトソン研究所のFranaszekは，この問題に取り組んでおり，制約が図1のように有限有向グラフで表現できるとき，そのグラフを頼りに符号を構成する方法を提案していた．非常に巧妙な方法であり，多くの場合に良い結果を与える方法であったが，どのような制約に対して適用できるのか，その方法を適用可能な制約の種類は明確ではなかった．

　この符号構成の問題は，Adler，CoppersmithとHassnerによって，あるクラスの制約に対しては厳密に解かれている⁽⁵⁾．

［定理4］有限形（後述）の制約が与えられたとする．，を正整数としたときであれば，符号化率がであるような有限状態符号器が存在する．そして，その復号器はブロック写像（以下に定義する）として与えられる．

　この定理は，記号力学系（数学の一分野）に関する結果を応用して得られている．

　この定理の証明では，構成的に符号器を与えられており，それに従って設計した符号器が実用化された^(5)～(7)．

［定義5］を，有限集合とする（以下では，アルファベットと呼ぶ）．を，の要素から成る，全ての有限系列の集合とする．空系列も含むとする．を，ある有限系列の集合としたとき，を以下のように定義する．

には，のどの要素も生じない

これを記号力学系と呼ぶ．が有限集合であるとき，は有限形であるという（条件については例えば文献(８)）．有限形力学系は，ある性質を持ったラベル付き有限有向グラフによって表現できる．その性質を持ったによって定まる力学系を，と書く．のとき（何も制約がないとき），フルシフトと呼ばれる．

［定義6］ブロック写像

　ある力学系から別の力学系への写像が，次の性質を持つとき，はブロック写像であるという．ある写像が存在して，全てのとに対して

が成立する．ここでは，の番目の要素を意味している．とは，それぞれとの記号アルファベットである．

　がブロック写像であるということは，は，を含む，長さがの周辺のパターンから定まり，その規則は場所（添字）には依存しない，ということを意味している．

［定義7］力学系に対して，となるような有限集合とブロック写像があるとき，はソフィックであるという．

　符号器が有限状態符号であるとき，符号化規則が1対1でありさえすれば，原理的には，復号規則を定めることができる．しかしながら，ある時点で誤りが入ってくると，それ以降の復号に影響する可能性がある．これは誤り伝搬と呼ばれ，記録符号を構成するときには，一つの誤りが無限に伝搬することがないように構成することが重要であった．

　復号規則がブロック写像で与えられれば，誤り伝搬は必ず有限であることが保証できるので，定理4によって構成された符号は応用において重要な意味がある．

　定理4の証明は記号力学系の成果を利用しているが，実はその記号力学系は情報理論と深い関係がある．この点について，次に述べる．

2.2　情報理論と記号力学系

　Shannonは情報源のエントロピーを定義したが，これは，コロモゴロフによって，測度論的力学系のエントロピーに拡張された⁽⁹⁾．二つの測度論的力学系が同形であるかどうかを判定する問題は，この分野の基本的な問題である．エントロピーは，同形性の不変量であることが示され，同形性の判定問題に大きく貢献した．実際，ベルヌーイ形の測度論的力学系に対しては，エントロピーが完全な不変量である，つまり，エントロピーが等しいことと同形であることとは同値であることが示されている⁽¹⁰⁾．

　このように，情報理論で定義されたエントロピーは，力学系の分野に大きな影響を与えた．逆方向の影響としては，前述の符号構成法がある．この構成方法のアイデアは，整数に対してエントロピーがとなるような力学系と，記号数がのフルシフトとの間の埋込の問題を解くための証明方法にある．

　ある正整数に対して，ある有限形の力学系のエントロピーがであったとする．有限形の力学系は，有限有向グラフで表現できるが，Marcusは，エントロピーがであれば，全ての頂点の出次数（頂点から出ていく枝の本数）がであるようなグラフで定義される力学系と同形であることを証明した．そのグラフの各頂点から出ている個の枝に別々の記号を割り当てることによって，埋込を定義できる⁽¹¹⁾．その証明では，グラフの状態遷移行列の固有ベクトルを頼りにグラフの変形を行う．これは，状態分割法と呼ばれる．Adlerらは，これをエントロピーが以上の場合に拡張して符号を構成する方法を示した⁽⁵⁾．

2.3　周波数スペクトルに関する制約

　前述の符号構成法の応用例について述べる．

　ベースバンド伝送において，AC結合を使った電子回路で信号処理をする場合には，信号に含まれる直流成分が問題を引き起こす（例えばCD，DVDやイーサネットなど）．そこで，伝送路に信号を送信する直前に，信号が低周波数成分を持たないように符号化することがある．

　このような符号を設計するためには，信号が低周波成分を持たない，という条件を明確にする必要がある．とを記号とするブロック符号を考えた場合には，各符号語の記号の和がであることが，信号の平均値がであるための十分条件であることはすぐに分かる．実はこれが，周波数スペクトルの離散成分と連続成分が直流においてになるための必要十分条件であることが安田らによって示されている^(12),(13)．吉田らは，この結果を拡張して，記号周波数の有理数倍の周波数において，周波数スペクトルがになるための必要十分条件を与えている⁽¹⁴⁾．これらの結果は，指定された周波成分を含まない信号を生成するための基礎理論となった．ところで，安田らの結果^(12),(13)はPierobonによって⁽¹⁵⁾，吉田らの結果⁽¹⁴⁾は，MarcusとSiegelによって再発見されている⁽¹⁶⁾．

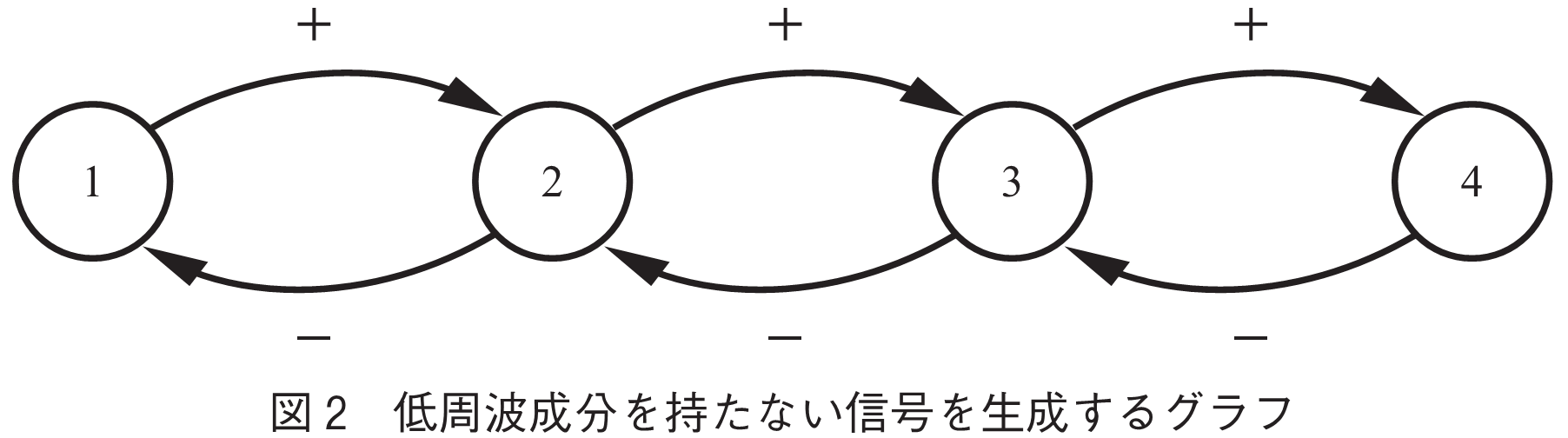
　CDとDVDでは，EMF，EMF＋という符号が使用されている．これは，四つの状態を持つ有限状態符号器である．グラフは，上記の文献の条件を満たすように作成され，ACHの状態分割法を用いて，窓サイズが2のスライディングブロック符号器によって復号できるように構成されている（文献(３)11章）．

　図2は，低周波数成分を持たない信号を生成するグラフであり，有限形力学系ではないソフィックになる．ソフィックに対しては，状態分割法を直接には適用することはできない．ソフィックを内側からエントロピーの意味で近似することができるので，そのようにして得られた有限形の力学系に対して状態分割法を適用することで，有限状態符号器を構成できる⁽¹⁷⁾．

3.1　二重化誤り

　は長さが0の系列（空列）を意味し，任意の系列に対して，はその長さを意味する．系列に対して，長さの接頭辞と長さの接尾辞は以下のように定義される．

　系列がと分解できるとき，系列は，からの二重化誤りによって得られる，若しくは，から長さの二重化誤りによって得られる，という．ここでである．

　二重化誤りの関数を次のように定義する：とを正整数とする．は

　DNAストレージのための誤り訂正符号を考えるために，誤り訂正符号を以下のように定義する．

［定義8］長さの二重化誤りのための符号とは，以下の条件を満たす符号である．

　1．，

　2．，

　3．全てのに対してとに，長さがの二重化誤りをどのように回適用したとしても，同じ系列になることはない．

　もしが，任意のに対して符号であるならば，符号であるという．

3.2　符号と連長制約

　次の写像を定義する．

［定義9］を，次式で定義する．

　ここで，である．

　詳細は省略するが，によって，二重化誤りとの連長との間に，一対一の対応を付けることができる．

　Jainらは，以下の定理10を証明している⁽²⁰⁾．まず，符号を次のように構成する．

符号の構成A：正整数に対して，

　このとき，次の定理が成立する．

［定理10］文献(21)上で定義した符号は，符号である．ここで

である．ただし，は，上の制約を満たす，長さがの系列の数である．

　DNA系列を工学的に利用するための符号理論の研究が進められているが，この結果のようにこれまでの制約などに帰着できるものもあれば，全く新しい体系を必要とするものもある⁽²²⁾．

4.1　WOM符号

　RivestとShamirは，書換えができない記録媒体を使って，複数回の記録を行うための符号（WOM符号）を提案した⁽²³⁾．フラッシュメモリは，書換え回数が有限な記録媒体であるため，WOM符号を，フラッシュメモリにうまく適用できる．WOM符号については様々な研究が行われているが，実際に適用するためには，現在の方式を大きく変更する必要があるため，実用化には至っていない．

　Sharonらは複数の電荷レベルを認識可能なフラッシュメモリ（MLCやTLC）の信号処理にWOM符号の考え方を適用することで，セルの電圧を効率的に読み出せることを示した⁽²⁴⁾．ここでは，その考え方について述べる．この方法は，現在のフラッシュメモリへの書込み規則を若干変更するだけで実装でき，メリットも大きいため，WOM符号が実用化される最初の例になる可能性が高いと思われる⁽²⁵⁾．

4.2　ランダム入出力符号

　TLC（Triple Level Cell）では，一つのセルに3ビットのデータ，，を記録することができるが，各ビットは独立したページのデータとして扱われる．つまり，はページのデータとなり，各ページの内容は独立にアクセスされるとする．

　電圧レベルとビットパターンと対応表は，表1に与えられている．電圧が，参照電圧と比較して高いか低いかを確認することでビットパターンを読み出す．具体的には，ページ0の情報を読み出すには電圧4より高いかどうかを確認すればよい．ページ1の情報を読み出すときには，電圧が2と5の間にあるかどうかを確認する，などである．このようにすると，ページ1の情報を読み出すためには2回の電圧の比較が，ページ2の場合には4回の比較が必要になる．これがMLCの速度を遅くしている原因の一つになっている．

　表2に，RivestとShamirが示した，からへの変化が1回しかできない三つのセルを使って，2ビットの情報を2回書くためのWOM符号の符号化規則を示している．この表に基づいて，と三つの電圧レベルを区別できるセルを三つ使って，2ビットの情報を二つ書くことを考える．一つ目の情報は，WOM符号の1回目の規則で，二つ目の情報は，WOM符号の2回目の規則で求め，それらを足し算した値をセルに書く．ただし，一つ目と二つ目の情報が同じ場合には，一つ目の情報を2倍した値を書くとする．例えば，一つ目の情報がで，二つ目の情報がであれば，が書き込まれる．この規則を表にしたのが，表3である．

　セルに注入する電荷を計算するときに，という計算はないので，以下の規則で復号できる．

一つ目の情報の復号：2を1に，1を0に変換して，WOM符号の規則で復号する．

二つ目の情報の復号：2を1に変換して，WOM符号の規則から復号する．WOM符号の2回目の符号語でない場合には，1回目の符号化の規則から探す．

　一般に回書込み可能なWOM符号を使用したときには，各セルについて1回の電圧比較を行うだけで，番目のページの情報を読み出すことができる．

　Yaakobiらはこのアイデアを発展させて，より符号化率の高い符号化方法を提案している⁽²⁵⁾．Sekiyaらは，これと同じアイデアを多重アクセス通信路に対して適用している⁽²⁶⁾．