1．は　じ　め　に

　システム・数理領域の研究においては数値的なスペックや実験結果の明示よりも提案する手法・技術，その着眼点，仕組み，効果などに対して論理を積み重ねて，誤りなく，かつ，分かりやすく説明することが極めて重要である．また，数値的な評価結果も重要なものではあるが，その評価軸設定の理由やその数値や実験結果の意味するところ，手法の有効性，研究を進めるにあたって定めた仮設の検証など論理を組み立てた説明が行われていないと提案する手法などの有効性が主張できない．

　このように論理を組み立てて表現する手法は，システム・数理領域など研究成果を論文として残す際において必要不可欠な事項であるが，読み手を納得させる汎用的な表現法を含んでいるため，研究者・技術者の社会生活における報告書，提案書，計画書を記述する上でもとても役に立つことも多い．本稿では，システム・数理領域における論理を組み立てる研究，それらの中で利用される各種手法，研究者・技術者の社会生活での活用法などについて述べる．

2．システム・数理領域の研究とは

　本稿の目的である論理を組み立てるという作業は，一般の文書書類作成にも不可欠な要素であるが，電子情報通信の領域とりわけシステム・数理領域の研究の観点で説明を行う．このため，まず，システム・数理領域の研究の特徴について説明を行う．

　システム・数理の問題は，現実の課題を数理的に扱えるモデルに変換し，変換されたモデル上で数理的，情報処理システム的処理を行い現実の課題にフィードバックするものである（図1）．現実の課題へのフィードバックにはいろいろあるが，主なものは，一つの指標，あるいは複数の指標を同時に目標とするゴールに向かって最適化を行う最適化問題を筆頭⁽¹⁾に，設計や作業など手順などの指針の作成を行うもの，認識を行って対象物を特定するもの，現状の分析を行って処理の流れの見える化を行うもの^(2),(3)，解析を行って原因を特定するもの，シミュレーションを行って予測を行うもの⁽⁴⁾などが代表的である．しかし，このモデル化→数理的処理→現実課題へのフィードバックの過程では2点問題がある．一つ目の問題点は，現実問題と全く同じモデルの作成が困難である場合が多いことである．回路を方程式で表現するSPICE⁽⁴⁾などは極めて現実の回路に近い物理的モデルを再現可能であり，実用的には現実の回路にほぼ同等の方程式モデルを作成している．しかし，SPICEの事例においても解導出の高速化などのために，方程式モデルの一部を近似したもので置き換えることがある．すなわち，課題をモデルとして表現する際，モデルが複雑になるなどの理由で近似や省略が導入され，実際解くべき課題を正しく反映できない場合もある．また，問題の解きやすさからモデルの制約を強化する場合も多い．このような，全ての課題をそのまま正確にモデル化することは困難であるような場合に対しては，その近似性や省略に関して，モデルの有効性に対して論理を組み立てて説明して主張すればよい．例えば，現実の課題とモデルの間には多少のかい離が存在するが，実用上問題ないことを論理立てて説明する．あるいは，目的の解を高速に得るために，一部のモデルを簡易的なもので置き換えるなどを，その目的においては妥当であることを説明する．このとき論理飛躍などがあると，「自ら提案する手法に合わせて課題を設定した」という印象を与えてしまうので要注意である．

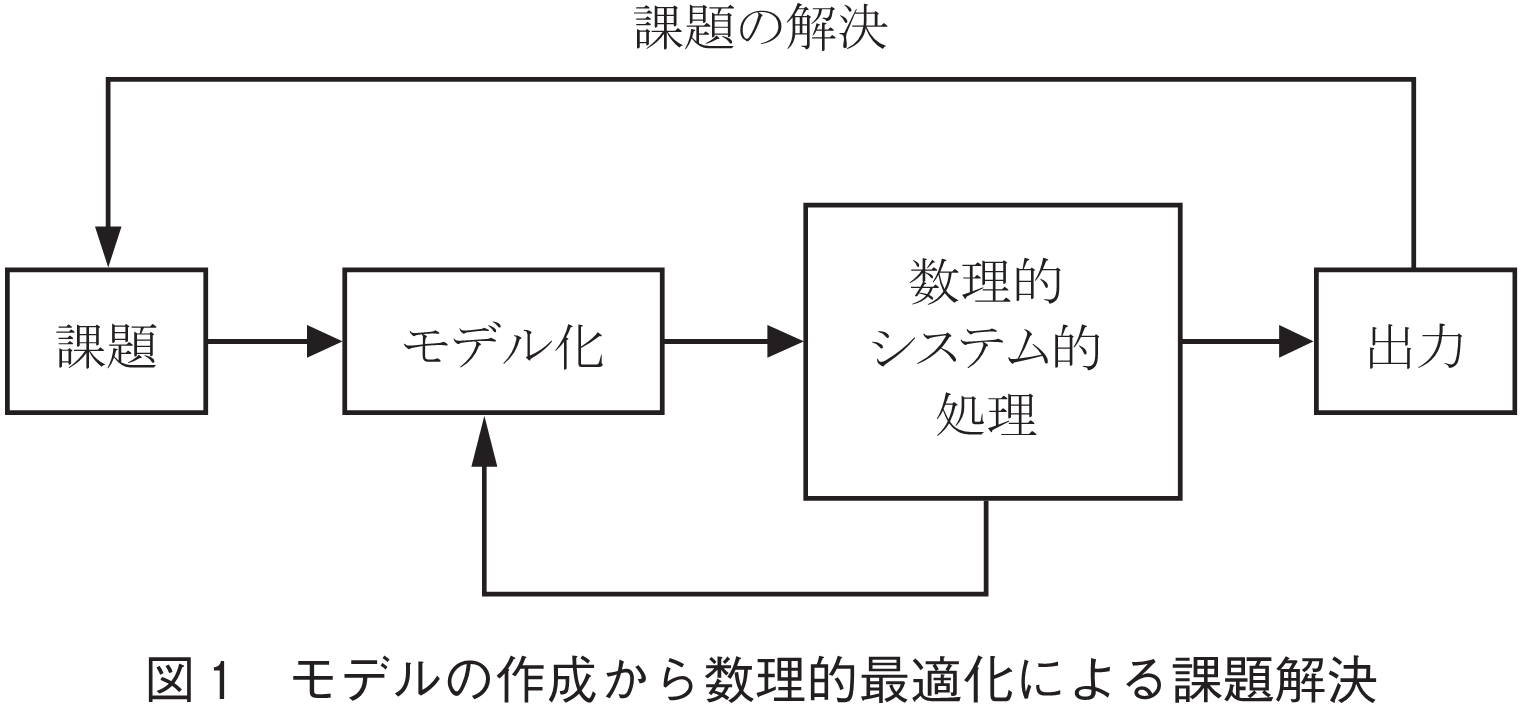
　二つ目の問題は後述のように，モデル化された問題が数学的に完全に要求を満たすように解ける場合が少ないという問題点である．この場合は，与えられた，あるいは仮説的に考えた制約の中で現実的な時間やリソースで問題を解決することになる．その場合，現実的な時間やリソース，あるいは自ら設定した制約におけるベストの解に対する有効性に関して同様に論理を組み立て説明することが必要となる．例えば，有名な巡回セールスマン問題⁽⁵⁾は，セールスマンが巡回すべき点を最小コストで全て訪れるという問題である．この問題は巡回すべき点を重み付枝で結んだグラフ理論の問題にモデル化し，グラフ上での全ての点を最小重みで巡回する問題を解くことになる．現実問題においてトラックの配送問題として実際の問題に適用しようとすると，そもそもグラフでのモデル化が適切か，あるいは，巡回すべき点間の重みの設定の問題など，実際の問題で受容でき得る解が得られそうか，などの観点で一つ目の問題であるモデル構築の難しさがある．更に，二つ目の問題点である数理的な最適化が困難な場合に，構築したモデル上にどのような手法を使って数学的に最適に解くかという点でも工夫が必要である．その工夫の妥当性をいかに論理立ててうまく説明するかがポイントである．このように，モデル化と数理な処理を行ってシステムを構築するシステム・数理領域において，論理を組み立てて説明し納得を得るというのが研究を進める上でも，論文・発表の観点でも重要となる．

3．システム・数理領域における論理の組立て

　研究成果において数値的な優位性の主張は重要である．例えば，従来よりも2倍の高速化であるとか，30%の低消費電力化，使用するメモリを1/10にするなど，従来手法などとの数値評価を行うことでその研究の有効性や新規性は一目瞭然となる．それらの数値が等しい条件で従来研究よりも優れており，その数値を達成するための手法に従来にはない新規性のある手法・技術が含まれていれば，その研究は有為な研究となる．一方，数値的な優位性のみが主張され，その数値を達成するための手法の説明が詳細でなくても論文や研究発表として成立する場合がある．それらはその数値の特性から，その数値を達成するための筋道がその専門家には予想が可能であることで，詳細な説明がなくてもその有効性や新規性が確認可能であるため，暗黙の了解の下で論理説明が省略可能である．また，その数値を観測するためには試作品などの‘もの’作りが必要となるため，その研究成果物を開発するにあたってのノウハウを文章や図として表現できない場合がある．その場合は，‘もの’作りを行い，それらが動作したことの証明が論理立てた説明を表現していることになる．同様に，評価方法や成果物の開発方法が研究者のコミュニティではほぼ定まっており，その研究成果の競合との比較が容易であることもある．（100メートル競走のように，誰が見ても勝敗が明らかになる．）結果的に，数値や実際のシステム，装置によって有意性を主張できる研究の場合は，研究成果のスペック，性能，成果物の写真や評価結果を提示するだけでも十分に研究成果の新規性・有効性を表現できることもある．しかし，システム・数理の研究においてはこれらの事例は極めてまれである．

　システム・数理の研究においては，研究成果の数値によるアピールは重要であるが，数値による研究の評価が良くても，それだけで新規性・有効性がある研究と認定されない場合が多い．「なぜそのような良い結果が出るか？」に対して納得性が得られることが最も重要だからである．それができないと，良い結果は提案手法により得られたのではなく，偶然得られた，あるいは偶然良いデータに当たっただけという評価を受ける場合すらある．一方で，そのような納得性のある説明ができれば，仮に数値的に悪い評価結果が出たとしても高い研究価値が発生する．すなわち，悪い評価結果が得られた原因，理由，及び，対象データ・特定データにおける有利な点，不利な点を論理立てて説明することによって，後に続く研究者に対して提案手法が採用したアプローチのどれかが，特定の場合では有効であり，別の場合では余り有効ではないことを示すことができるからである．

　実際，システム・数理の研究においては評価すべき項目が多く，それら全てにおいて従来研究に勝る研究成果などあり得ない．たくさんの評価項目の中で，どの評価項目に着目して成果を出そうとしているかに関しては，想定する仮説や応用，現実の課題に即して論理を組み立て，説明しておく必要がある．例えば，計算機を使った最適化問題や機能実現問題は，一般的に良い答えを出そうとすると計算時間や計算のためのリソースを多数必要としてしまう．しかし，現実的な応用を考えると，仮に性能が10%良くても数か月の計算時間が必要であれば，5%の性能向上で1時間の計算時間を必要とする方が一般的に実用性は高い．もちろん，応用によっては1%でも良い性能に対して数か月費やしても妥当な場合もある．それらは全て応用における課題によって決定されてモデル化の際に考慮される．

　例えば，組合せ最適化問題においては，ほとんどの問題はNP困難⁽⁶⁾に帰着されて厳密に最適な解が得られない場合が多い．そのような場合は，問題が大規模になるに従ってほぼ無限の計算時間が必要となる厳密的な解法の代わりに，実用的な時間での解決を行う発見的な近似解法を用いることになる．一般的な近似解法は，ある事例に関してほぼ厳密解に近い結果を出すが，全ての事例に関して良好な結果を得られず，すなわち，ある特定の例で結果が悪かったり，処理時間が非常に長くなったりする場合がある．しかも考えられる全てのデータでの数値的（最適化目標，処理時間など）な評価を行うことは難しく，応用上不可欠な代表的なデータや指定されたベンチマークなどでの評価となってしまう．それ以外の場合がどうなるかを示すために，提案する手法の特徴から論理を組み立てて，どういう場合は有効に働き，どういう場合は有効ではないかを読み手に理解してもらう必要がある．この場合の説明は，提案する手法の構造的傾向と，代表的なデータに対する数値的な結果の傾向を組み合わせて論理を組み立てると説得力が増す．更に，これを多数ある評価項目別に評価を行うことによって更にその研究の価値を高めることができる．

　もちろん，システム・数理以外の領域においても上記のように，提案する手法や技術の傾向と数値的な結果の両方を組み合わせて論理を組立て展開することは，良い表現方法である．

4．論理を組み立てる論文，申請・提案書などで気を付けておくべきこと

　主にアカデミアにおける競争的獲得資金を得るために申請書の作成，企業における各種提案書，報告書を書く際にはそれらの書類の納得性・了解性の品質が厳しく評価される．その際に重要なのは，それらの読み手に論理を丁寧に組み立てて違和感を持たせないことであると言える．筆者の経験から，これら申請・提案・報告などの書類で違和感を持たない論文や申請書のポイントは，①主張点にぶれがなく論理に筋が通っていること，②唐突な話題の転換なく文章がつながること，③厳密性を担保する数式やアルゴリズムに対して適切な説明が述べられていることである．

　論文や申請書などを作成する際，全体の物語として筋が通っていることが最も重要である．例えば，箇条書きで流れを記載してみて筋が通っていることを確認しながら，読み手が受ける感触を検証することも重要である．全体の筋が通っているかどうかを確認するためにアウトラインプロセッシングツールを使うこともよい．アウトラインプロセッシングの一部機能は，一般のワープロソフト，プレゼンツールやテキストエディタにも搭載されていることが多いのでそれらを利用すればいいだろう．要は章立てと，その中で何を記載するかを記述しておき，主張すべきことが全て書いてあるか前後の章との関連性に誤りがないかを確認しておく．

　次に，具体的な文章のつながりに関して述べる．それぞれの文章が有機的に結合されて，主張すべきことが構成されている必要がある．その際必要とされていることの脱落や，あるいは，相反することを両方記載してしまってその研究がどの方向を目指しているか不明確になっていないか，同じことが重複して記載されてないかを確認する．下記の点に注意して論理構築を行うとよいだろう．

 （１） あらかじめ設定された課題が解かれていない．推理小説の伏線設定，伏線回収に相当する記述がない．あるいは，課題を記載しているつもりであり，課題が解決されていることになっているが実際は課題が書かれていない．（このため筆者は若手研究者に良質の推理小説を読むことを推奨している．その際にロジカルに伏線が回収されているか，いわゆる後出しが行われていないか，などをチェックしながら読むようにも推奨している．）

 （２） 文のつながりに飛躍や相反などがある．ある主張をしておき，その主張の問題点を指摘することにより，自分の主張を述べる場合（but, however, although）．ある主張の理由を後ろの文で述べる場合（because, since），前の文の説明を更に詳しく説明する場合，例を示して説明する場合（then, thus, for example）などを自分で意識してどういうつながりになっているかを適切な接続詞が使われているかを確認しながら論理を組み立てる．

 （３） 文章中に唐突に別のことを主張していないか，あるいは，風が吹けば桶屋がもうかる的に説明すべきステップで省略された（図2）ものはないかを確認する．こういった唐突感やステップの省略が発生した場合，論理が飛躍していると指摘される．

 （４） 実験を含めて評価を行う場合は，その評価軸は提案する手法に期待されている評価方針と合致していることを確認する．例えば，計算時間の短縮が目的の研究において，メモリの使用量を第一評価軸とすべきではない．メモリの使用量削減がもしも実現されたとしたら，それは副次的効果である．

 （５） 実験などによって数値的評価を行った場合は，提案する手法や機能との関係性を必ず述べ，提案する手法や機能が実現され，当初期待されている性能・効果が実現できていることを主張する．更に，想定外の結果や他と比べて傾向が異なる結果が得られた場合には，多少の推測や想像が入っても構わないので，その理由を説明する．もしも検証が不十分になった場合は仮説検証により推測を述べる．更に，実験を行っていないデータに関しても，どのような傾向で結果が得られるかを推測するともっと良い．

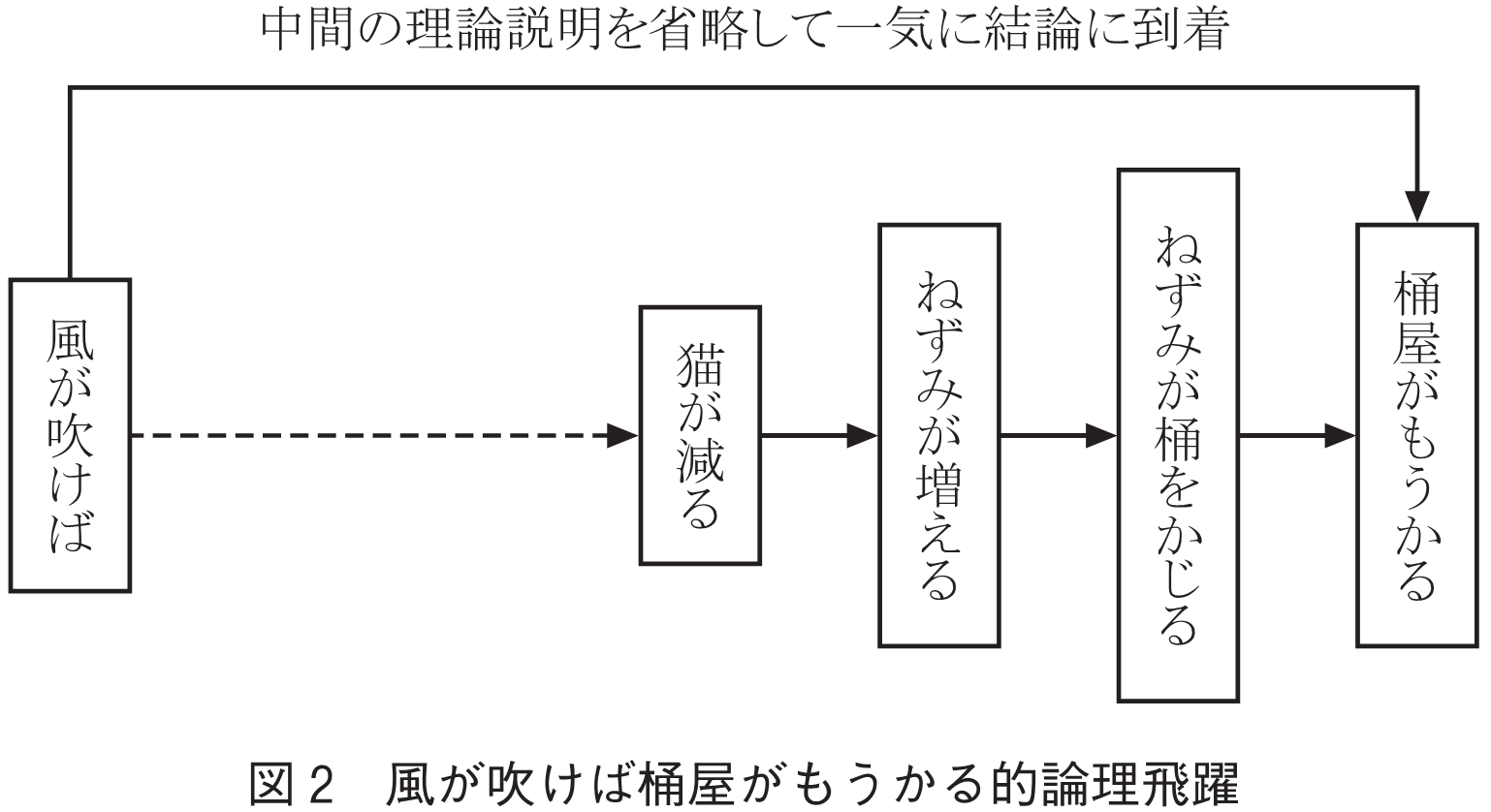
　加えて，システム・数理研究者には，数式やプログラムライクなアルゴリズムの記述に頼らない表現方法を身に付けることをお願いしたい．数式やプログラムライクなアルゴリズムの記述は，モデルの表現や最適化関数，処理手順を誤りなく厳密に記載するためにとても重要である．研究者としては，数式などを使って極めて厳密に記載したのだからそれ以上の説明や解説は不要であると考えがちであるが，提案や主張は相手に受け入れられて初めて価値が発生する．厳密性を示すための式やアルゴリズムだけでは読み手に大きな負荷を与えてしまい悪い印象を与えてしまう．すなわち，それらが研究の有効性，新規性の表現として読み手に理解されるためには，読み手側にその領域に対して深い理解や知識がなくても伝わる工夫をすべきである．例えば，プログラムを書く場合は設計書や仕様書あるいはフローチャートがあって，プログラムの開発が開始される．すなわち，アルゴリズムの説明にプログラムライクなアルゴリズムを記載することは，仕様書やフローチャートなしに，ソースコードのみでプログラムを理解せよというのと同じことである．数式の場合も同様で，数式からモデルや提案手法のコンセプトを理解せよというのは，上記のような「風が吹けば桶屋がもうかる」的な，中間論理をスキップした説明をしていることと同様であると筆者は考える．それら，数式で表現されるモデルやアルゴリズムを記載するその場合には，絵を使うか（筆者の友人のプリンストン大のMalik先生は一つの絵には1,000語の意味があると指導してくれた），あるいは文章で，その式やプログラム的の各項や中間結果の意味付けを説明するとよい．そのような説明を行うことで，提案する手法の意図や効果を正しく読み取ってもらえるという効果もある．もちろん，数式やプログラムライクアルゴリズムの直接的な記載があっても構わない．しかし，概念的にモデルや提案手法のメカニズムの説明を併記すべきであると考える．

　このように，論理を組み立てる研究の経験を積んでおくことは，現実社会で直面する申請書，提案書，報告書などの自身の見解や主張を表現する際には非常に有効である．

5．さあ，始めよう

　このような論理を組み立てる研究の経験を積めば積むほど理屈っぽくなり，日常会話において細かいこだわりが目に付き，研究者以外とのコミュニケーションにおいて「理系らしい」と揶揄される場合があるかもしれない．しかし，これらは褒め言葉と思って注意力を研ぎ澄まし，常に読み手のことを考えた表現を心掛けてほしい．そのためには，一旦文章などを書いたら一切その論文などに触れずに一晩，二晩寝かしておき，改めて読み直すとよい．そうすることで，自身を第三者的な客観的な読み手として自身の書いたものを点検でき，自身の論理展開が十分かどうかをチェックできる．

　なお，筆者も論理を組み立てる研究に関して，100点満点で論理を組み立てて説明できるようになったかというとまだ学習途中であると感じる．ちょっと気を抜くと筋道が通ってなかったり，論理の飛躍が発生していたり，読者に唐突感を与えてしまったりということが起きる．論理を組み立てる修行はどこまでも続いていくものである．

　さあ，意識して論理を組み立てることを始めよう．

文　　　　　献

　（平成29年2月5日受付）