1．は　じ　め　に

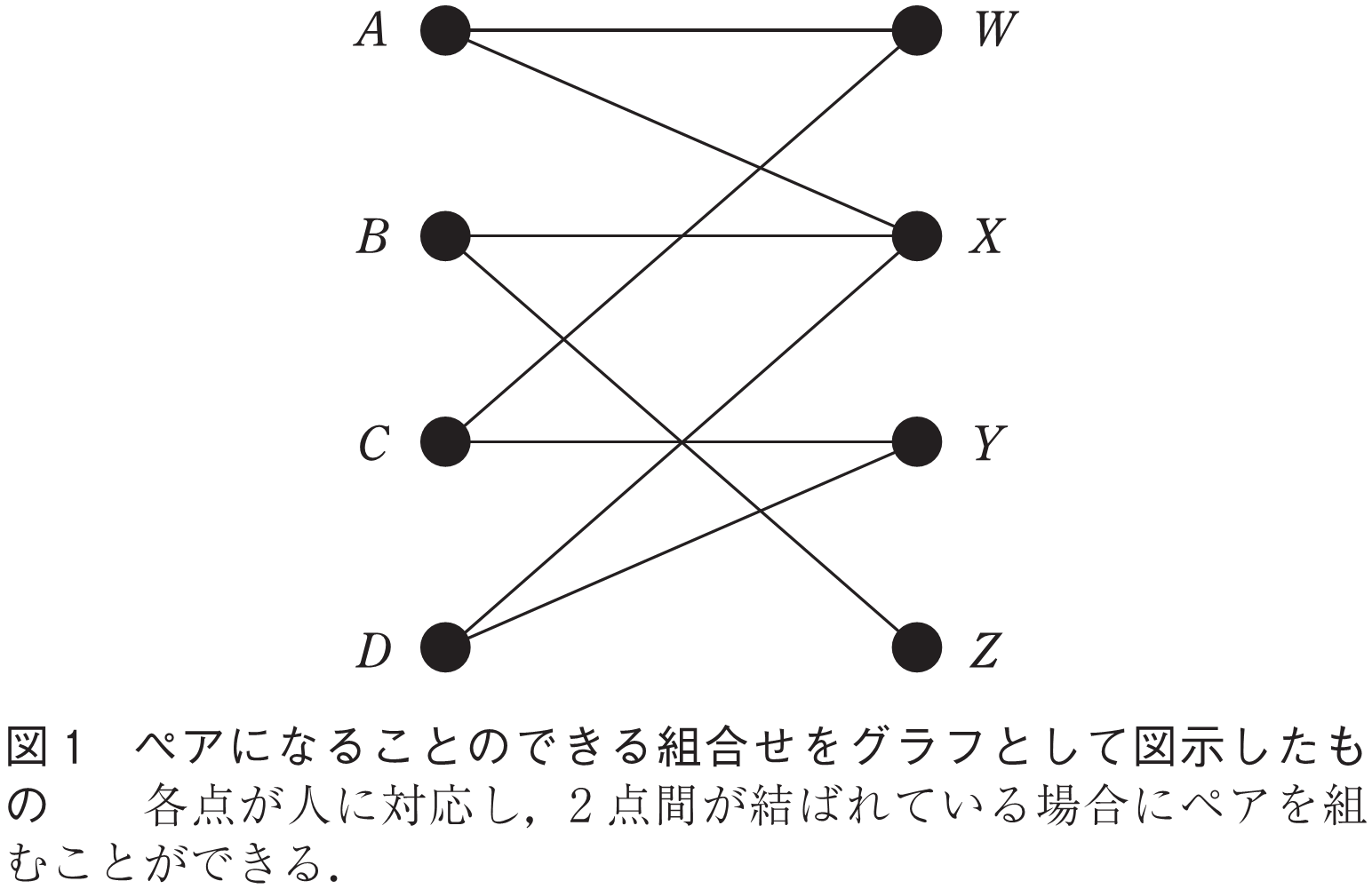
　4人の男性，，，と4人の女性，，，がいるときに，この8人を四つの男女ペアに分けることを考える．ただし，ペアになることのできる男女の組には制限があり，例えばとはペアになることができるが，とはペアになることができない，といった具合である．それぞれの人を点で表し，互いにペアになることができる人を線分で結ぶことで，ペアになることのできる組合せを図1のように表現することにする．この場合は，8人を例えば，，，というペアに分けられることが分かる．なお，図1のように点とそのつながり方を表現する構造はグラフと呼ばれる．

　本稿ではグラフを頂点集合と辺集合との組で表す．特に，今回の場合には各頂点に対応する人は男性と女性の2種類に分けられており，男女をペアにする状況を考えていた．そのため，扱うグラフは頂点集合がが2種類の集合，に分割されており，各辺はの頂点との頂点をつないでいる．このようなグラフを2部グラフと呼び，と表す．ペア分けはグラフにおいてはマッチングと呼ばれる概念に相当する．辺の集合がマッチングであるとは，どの頂点に対してもその点に接続するの辺が高々1本であることを言う．また，特にどの頂点に対してもその点に接続するの辺がちょうど1本であるときに，は完全マッチングであると言う．すると，男女ペアに分ける問題は，2部グラフが与えられたときに，完全マッチングを求める問題として記述することができる．