1．は　じ　め　に

　15パズル，箱入り娘，ラッシュアワー等のパズルで遊んだことがある方も多いであろう．これらなじみの深いパズルにも関連する「組合せ遷移」と呼ばれるトピックが，近年盛んに研究されている．

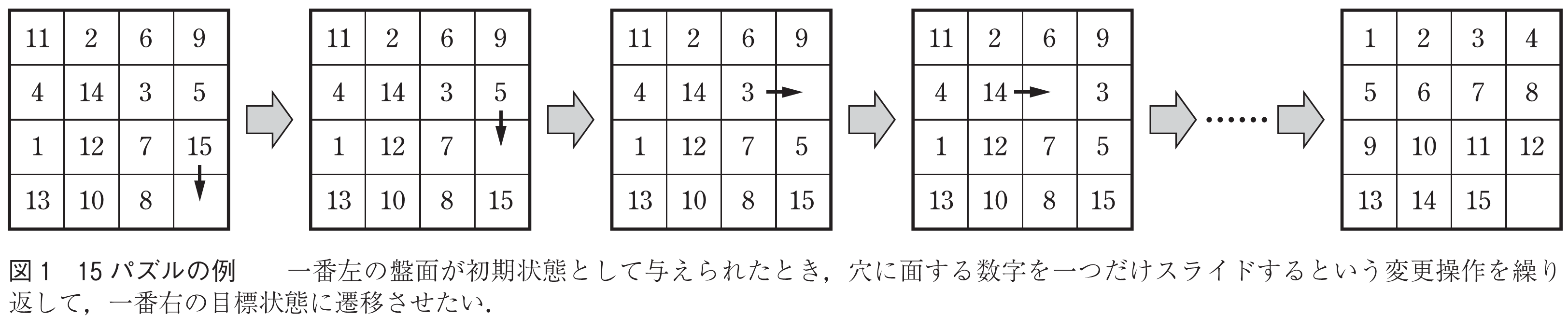
　組合せ遷移の枠組みは，動的な状況を定式化することに適する．大まかには，「初期状態」からスタートし，「許された変更操作」を繰り返しながら，「目標状態」に遷移させたい，という枠組みである．（15パズルの例を図1に示す．）詳細は後述するが，ここでいう「状態」とは「実行可能解（制約条件を満たす解）」を意味しており，遷移の過程で現れる状態もまた，実行可能解でなければならない．従来研究されてきた探索問題の多くでは，実行可能解が一つでも存在するかが問われた．それに比べ，組合せ遷移では，実行可能解が形成する解空間における連結性や到達可能性が問われる．

　組合せ遷移は，様々な分野で研究がなされてきた．理論計算機科学の分野，特にグラフに関連する問題については，最近10年ほどで急速に研究が発展・深化し，その理論体系化が進んでいる．本稿ではまず，組合せ遷移の枠組みと研究背景を紹介する．次に，最近の研究動向を解説するとともに，組合せ遷移におけるアルゴリズム開発の難しさ（筆者としては，面白さ）をお伝えしたい．

2．組合せ遷移の枠組み

　前章で大まかに述べたように，組合せ遷移の具体的な問題は，「実行可能解」と「許される変更操作」の二つを指定することで定義される．本章では，例を挙げながら，組合せ遷移の枠組みを導入する．

　なお，理論計算機科学分野におけるトピック名を「組合せ遷移」といい，その具体的な問題を「遷移問題」と呼ぶ．また，混乱を避けるために，実行可能解が一つでも存在するかどうか判定する問題を「従来型の探索問題」と呼ぶことがある．