
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|
小特集 2.
完全準同形暗号の構成方法
How to Construct Fully Homomorphic Encryption
abstract
完全準同形暗号(FHE)とは,暗号化したままデータの処理を可能にする暗号技術であり,概念として40年ほど前に提案されたが長い間実現方法が見つからなかった.しかし2009年にスタンフォード大学のGentryが初めて構成法を考案し大躍進を果たした.本稿では,Gentryの2009年の論文と後続研究における構成方法の主なアイデアを紹介する.特に次の3点に焦点を絞る.まずは低次数関数の準同形評価に対応する,いわゆるSomewhat準同形暗号(SHE)方式の構成について述べる.次にGentryの提案したSHEからFHEへの変換手法・ブートストラップの説明を行う.そして最後に,ブートストラップよりコストの低いモジュラス切換手法について紹介する.
キーワード:完全準同形暗号,ブートストラップ,格子ベース暗号,近似最大公約数問題
本小特集第1章の記事で説明されているように,完全準同形暗号(FHE: Fully Homomorphic Encryption)とは,暗号文に対し任意の効率的な関数の計算を復号せずに行うことができる暗号方式であり,公開鍵暗号の発明後間もなく発表されたRivest, AdlemanとDertouzosの論文(1)において概念として提案された.しかし,その実現は困難であり30年間も未解決問題のままであった.その後,2009年のCraig Gentryの論文(2)で初めて構成方法が紹介され,暗号学の画期的な進歩とみなされている.本稿ではその具体的な構成方法,及びより最近の論文で提案された改良について説明する.
公開鍵・共通鍵を問わず,暗号方式(Gen(用語),Enc(用語),Dec(用語))がある関数の準同形評価に対応するということは,平文
を暗号化した暗号文
を入力とした効率的アルゴリズム
があって,そのアルゴリズムが秘密鍵
を持たずに平文
を暗号化した新たな暗号文
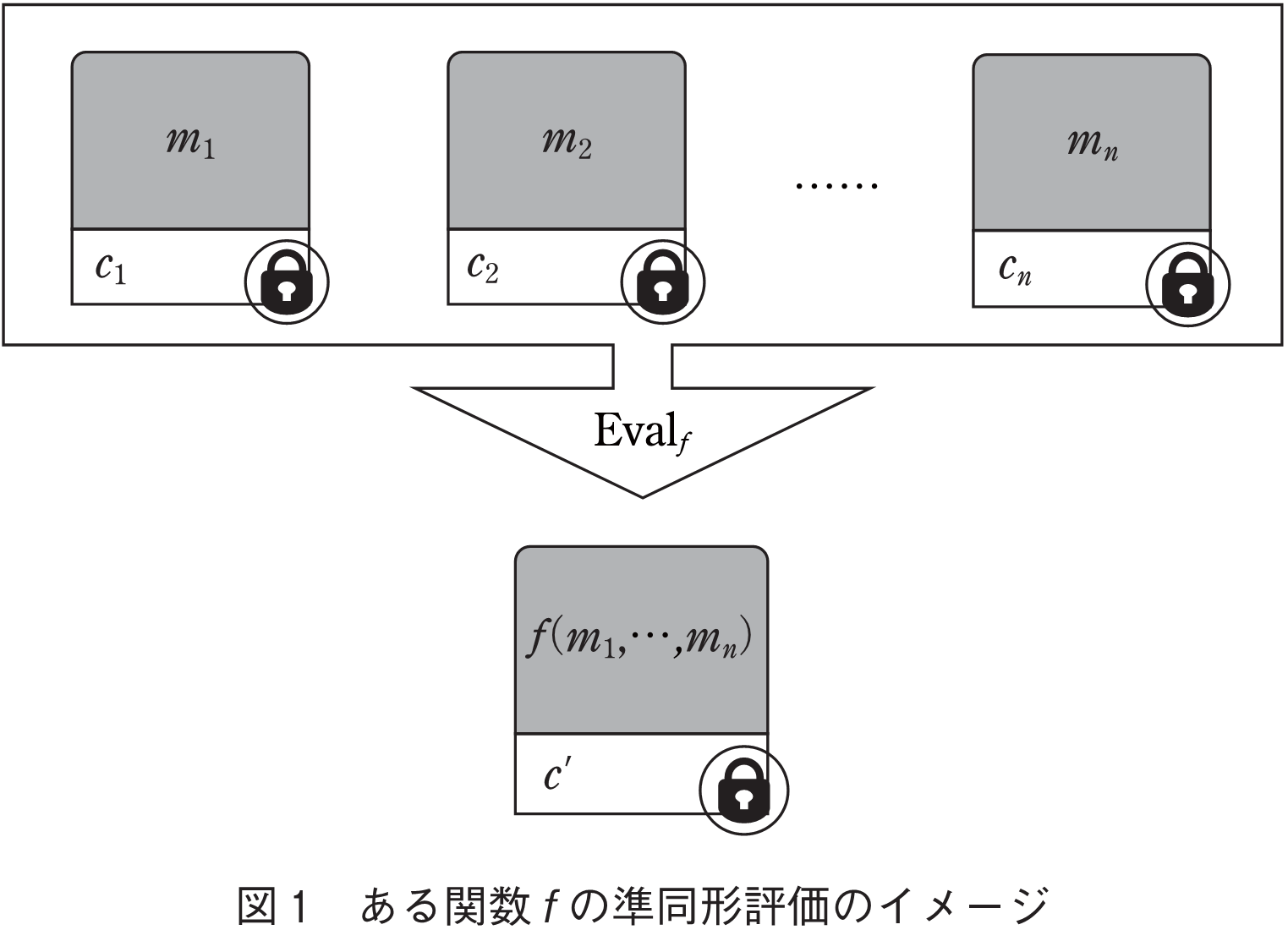
を計算できることを意味する(図1).つまり
が次式を満たす.
例えば,エルガマル暗号(3)は掛算の準同形評価に対応しており乗法準同形暗号方式という.なぜなら,エルガマル公開鍵をで示すと
の暗号文は
という形式があって,同形の暗号文
と成分ごとに掛算することによって
の暗号文
が求められるからである.同様に,Paillier暗号(4)は足し算の準同形評価に対応しており加法準同形暗号方式という.
続きを読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
「電子情報通信学会 - IEICE会誌」アプリをダウンロード