Vol.101 No.3 (2018/3)　目次へ

グラフアルゴリズムの最先端

小特集 4.

閉曲面上のグラフのハミルトン閉路

A Hamiltonian Cycle in Graphs on Surfaces

小関健太

小関健太　横浜国立大学大学院環境情報研究院社会環境と情報部門

Kenta OZEKI, Nonmember (Faculty of Environment and Information Sciences, Yokohama National University, Yokohama-shi, 240-8501 Japan).

電子情報通信学会誌　Vol.101 No.3 pp.258-261 2018年3月

©電子情報通信学会2018

abstract

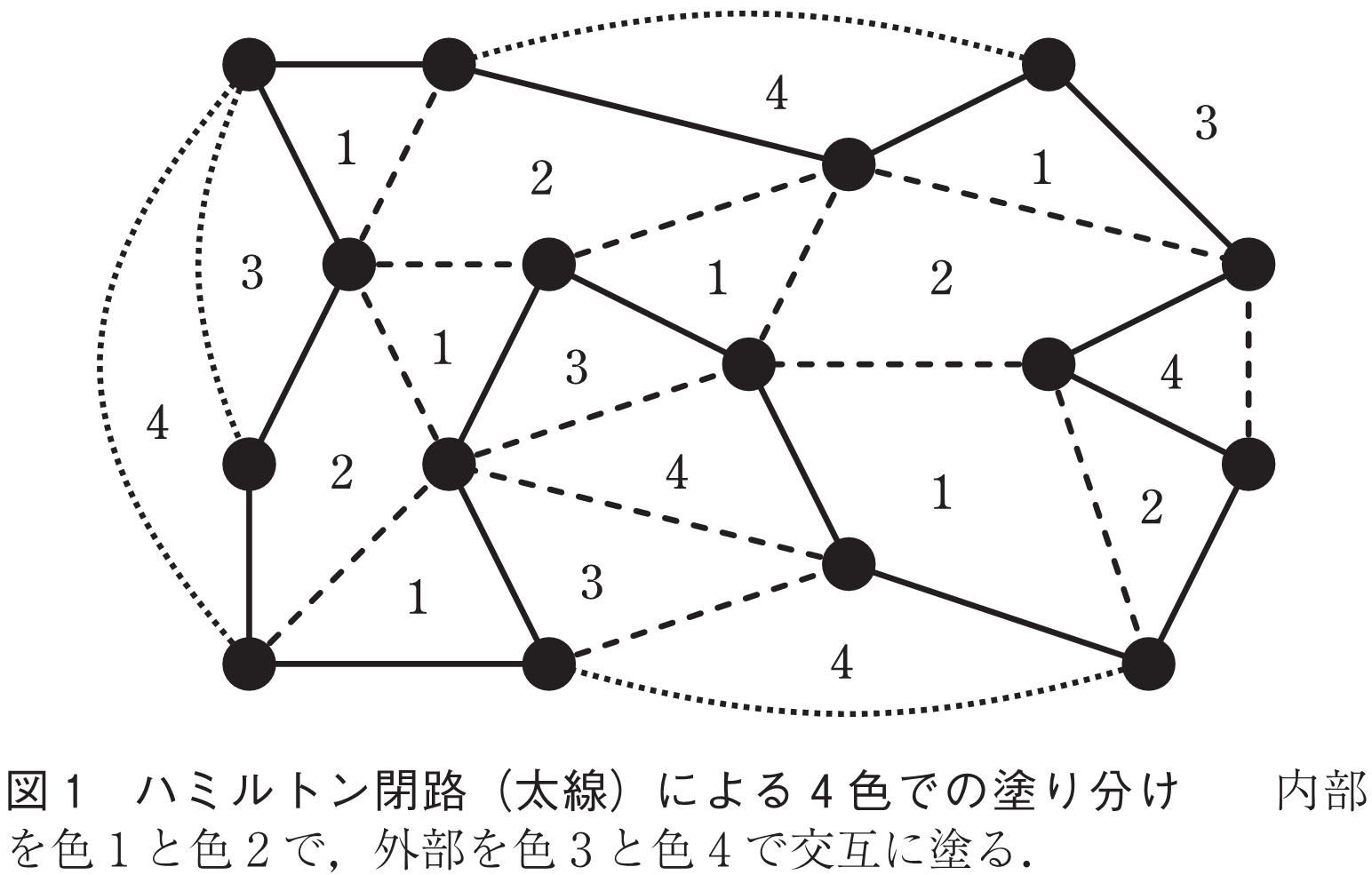
　与えられたグラフにおいて，その全ての頂点をちょうど一度ずつ通る閉路をハミルトン閉路という．平面グラフのハミルトン閉路問題は四色定理への挑戦の過程で提案され，また工学的な応用もあり多くの研究が続けられてきた．特に肯定的な命題として，Tutte⁽¹⁾は「4連結な平面グラフはハミルトン閉路を持つ」ことを示しており，この証明をベースに以降も多くの研究がなされている．

　本稿では4連結平面グラフにおいてハミルトン閉路を見つけるアルゴリズムのアイデアを述べ，当該分野の研究課題と彩色問題との関係について解説する．

キーワード：ハミルトン閉路，四色定理，平面グラフ，閉曲面上のグラフ

1．は　じ　め　に

　与えられたグラフにおいて，その全ての頂点をちょうど一度ずつ通る閉路をハミルトン閉路という（図1の太線を参照）．平面グラフ^(注1)のハミルトン閉路問題は，例えば2．の命題1にあるような“ハミルトン閉路を利用した彩色の手法”が開発されるなど，四色定理への挑戦の過程で提案され，多くの研究が続けられてきた．また，平面グラフのハミルトン閉路は，電子回路基盤での効率的な配線を与えるなどの工学的な応用も多い．

続きを読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。また、会員になると豊富な豪華特典が付いてきます。

続きを読む(PDF)　　　バックナンバーを購入する　　　　入会登録

電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。

電子情報通信学会誌会誌アプリのお知らせ

電子情報通信学会 - IEICE会誌アプリをダウンロード

小特集 4. 閉曲面上のグラフのハミルトン閉路

1．は じ め に

1．は　じ　め　に