Vol.101 No.3 (2018/3)　目次へ

グラフアルゴリズムの最先端

小特集 5.

メンバー間の距離が小さいコミュニティの発見

Finding a Community with Small Diameter

朝廣雄一　宮野英次

朝廣雄一　九州産業大学理工学部情報科学科

宮野英次　正員　九州工業大学大学院情報工学研究院システム創成情報工学研究系

Yuichi ASAHIRO, Nonmember (Faculty of Science and Engineering, Kyushu Sangyo University, Fukuoka-shi, 813-8503 Japan) and Eiji MIYANO, Member (Faculty of Computer Science and Systems Engineering, Kyushu Institute of Technology, Fukuoka-shi, 820-8502 Japan).

電子情報通信学会誌　Vol.101 No.3 pp.262-266 2018年3月

©電子情報通信学会2018

abstract

　人を頂点，友人関係を辺で表すことにより，人的ネットワークに対応するグラフ構造を考える．このようなグラフ構造に対して，緊密な関係にある人々のグループの中で大きなものを求めたい．緊密さとして様々な条件を考え得るが，グループに属する人々はお互いに直接の友人である，あるいは例えば友人の友人のように友人関係をたどると距離が小さい（ math 以下）という二つの条件に対応するクリーク問題と math -クラブ問題が知られている．本稿では近似アルゴリズムの観点から，これらの二つの問題，特に math -クラブ問題に関する研究動向について紹介する．

キーワード：クリーク，クラブ，近似下界，近似アルゴリズム

1．はじめに――クリークとクラブ――

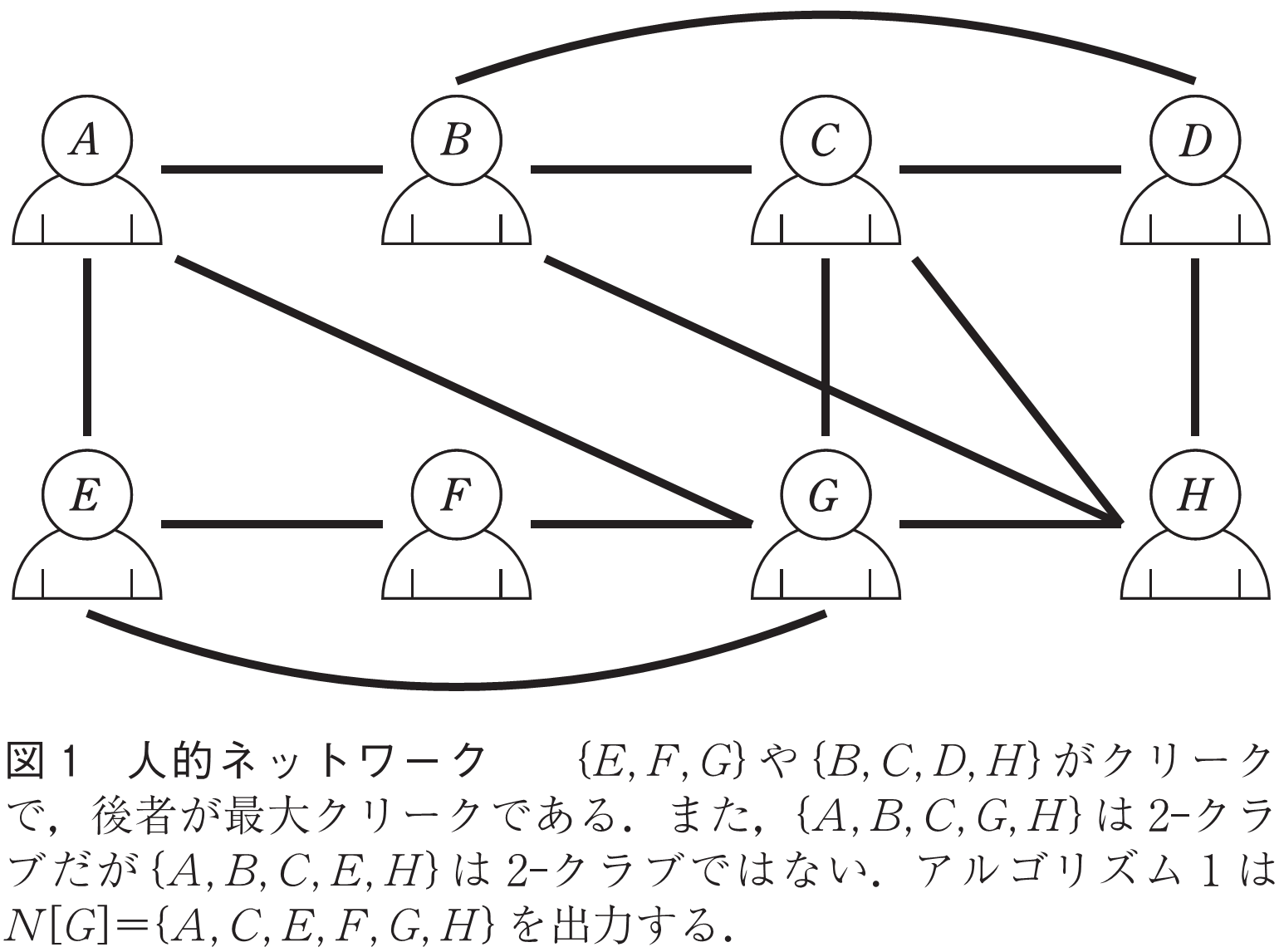
　人を頂点，友人関係を辺で表したグラフ構造を考える．図1がその例で，例えば， math さんと math さんや math さんと math さんは直接の友人であるが， math さんと math さんは直接の友人ではないことを表している．ソーシャルネットワークサービスの利用者が持つ友人関係から，このようなグラフ構造が定義できる．今，何らかの理由で（例：ターゲット広告），友人関係が緊密なグループ（頂点集合の部分集合，簡単に頂点部分集合と呼ぶ）のうちできるだけ大きなものを発見したい．緊密であることの定義方法はいろいろあると思うが，その頂点部分集合に属している人たちはお互いに直接の友人であると定義してみる．図1では，頂点部分集合 math が，そのような構造を持っているもののうち最大のものである．この構造はクリークと呼ばれ，最大のクリークを求めることを目的とするクリーク問題は理論計算機科学では超有名である．

続きを読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。また、会員になると豊富な豪華特典が付いてきます。

続きを読む(PDF)　　　バックナンバーを購入する　　　　入会登録

電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。

電子情報通信学会誌会誌アプリのお知らせ

電子情報通信学会 - IEICE会誌アプリをダウンロード