
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|
グラフアルゴリズムの最先端
小特集 6.
グラフ同型性判定問題への招待
Invitation to the Graph Isomorphism Problem
abstract
二つのグラフが「同じ」構造かどうかを判定する問題をグラフ同型性判定問題と呼ぶ.これは,グラフアルゴリズムにおける基本的なものであるにもかかわらず,その計算量が判明していない珍しい問題である.本稿では,この問題に対する既存結果や未解決問題,最近の進展などを紹介する.
キーワード:グラフ同型性判定問題,GI完全性
グラフは様々なものの構造を抽象的に表すものである.一見違うものに見えても,グラフによって抽象化されると本質的には同じ構造だったと分かる場合がある.では,「二つのグラフが表す構造が同じ」,またはより直接的に,「二つのグラフが同じ」とはどのように定義されるべきだろうか.グラフの同型性は,グラフが「同じ」であることを表す最も自然な概念であり,以下のとおり定義される.
グラフと
を考える.全単射
があり,
が成り立つとき,と
は同型であるといい,
と書く.また,このとき
を
から
への同型写像と呼ぶ.
直感的には,「もの同士のつながりを表す」というグラフの機能において,と
が同等であることが
により保証されており,多くの場面では,
と
を「同じ」とみなすことが自然である.
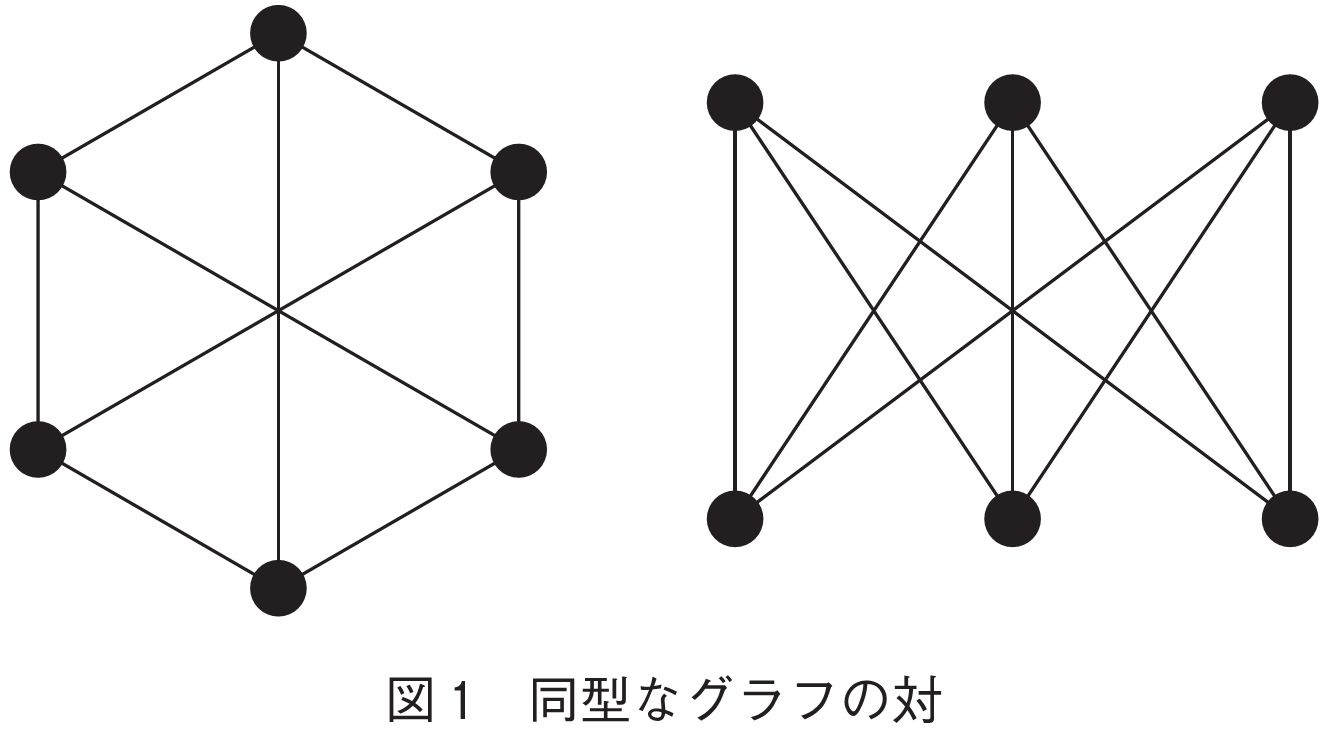
例えば,図1の二つのグラフが同型であることは,中列の2頂点の上下を入れ替える写像を作れば示すことができる.
続きを読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード