
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

2016年1月に閣議決定された第5期科学技術基本計画において,サイバーセキュリティ技術やビッグデータ解析技術,AI技術などを支える横断的な科学技術として数理的アプローチが注目を集めている.数理的アプローチとは,対象とするシステムに対して数理モデルを作成し,そのモデルを用いてシステムを考察する取組み方である(図1).
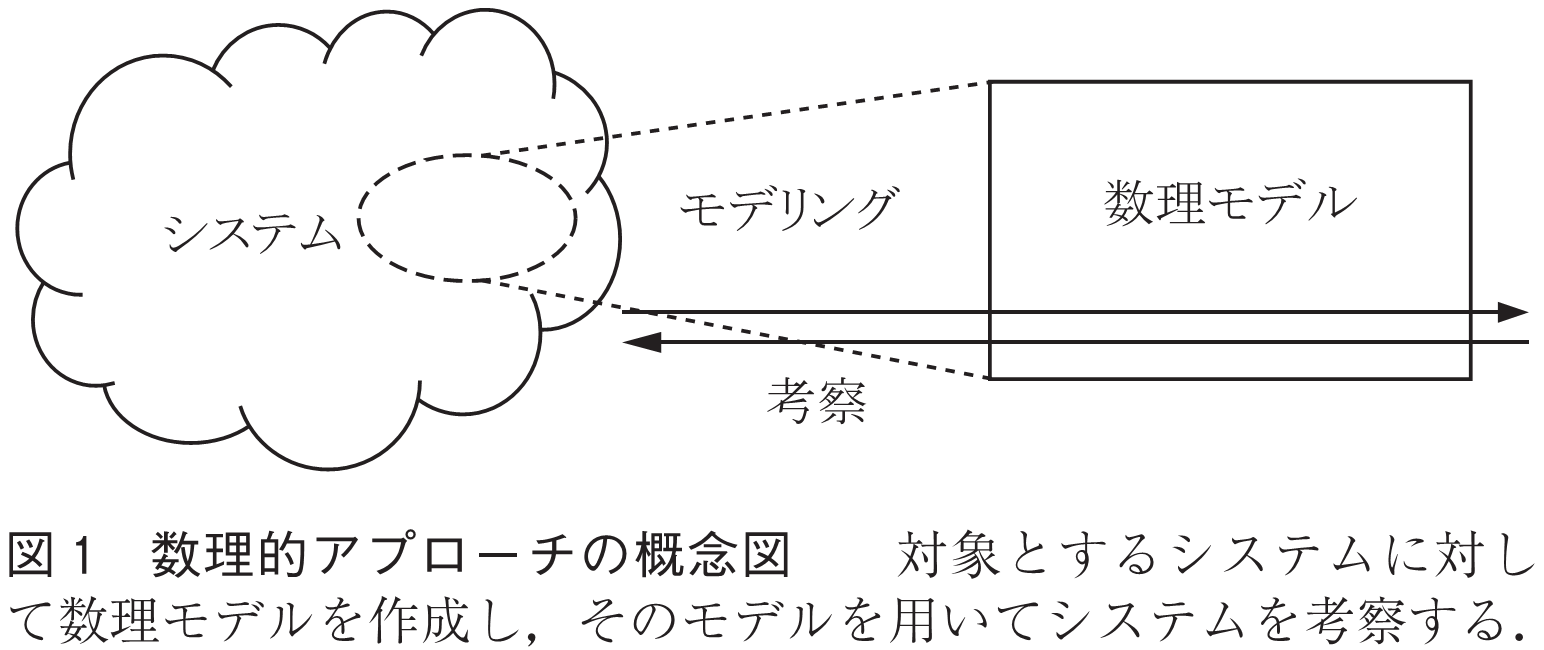
数理モデルとはシステムのある側面を数学の形式で記述したものであり,対象のシステムによって様々なものがある.計算機システムを対象としたチューリングマシンや,通信システムを対象としたシャノンの通信路モデルなど枚挙にいとまがない.モデルは通常,対象のシステムを簡略化したものである.したがってシステムそのものを対象にするより,モデルを対象にする方が考察が容易になる.例えば,対象のシステムを考察するための複雑さや危険性を軽減したり,不可逆性を回避したりすることを可能にする(1).
モデル化の基本原則は,いわゆる「オッカムのかみそり(Occam’s razor)」である.対象とするシステムの本質的な側面をより少ない変数で表せるモデルが,良いものとされる.モデルの表現力と解析力は通常,トレードオフの関係にある.このバランスを取ることが,数理的アプローチにおける一番の難関であり,醍醐味でもある.
数理的アプローチの一例として,ワークフローを対象とした筆者の取組み(2),(3)について紹介する.
ワークフローとは文字どおり,仕事の流れを意味する.ワークフローシステムは①仕事の流れを定義し,②その定義に従って,いつ,誰が,何をするかを指示し,③それらの間のやり取りを制御するシステムである.その応用例は,顧客対応業務から組織内部の承認・決済処理業務まで多岐にわたる.
ペトリネット(4)は離散事象システムのモデル化に適した数理モデルである.ワークフローのモデル化にペトリネットを使う研究は,古くは1970年代のZismanによるSCOOPに端を発し,1990年代後半になってvan der Aalstによって基礎理論(5)が築かれた.図2は注文処理のワークフローの定義を表すペトリネットモデルである.
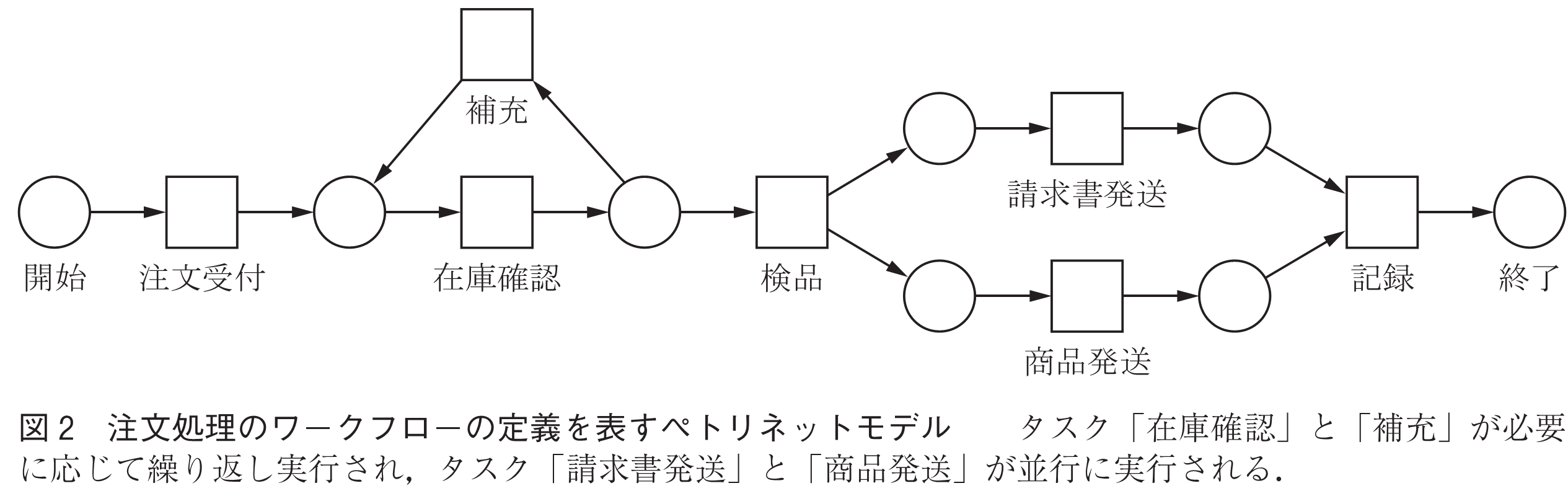
ペトリネットはプレース(○で描かれる)とトランジション(□で描かれる)という2種類のノードから成る有向二部グラフである.ワークフローのペトリネットモデルは単一の始点(プレース)と単一の終点(プレース)を持ち,各トランジションはタスクを表す.
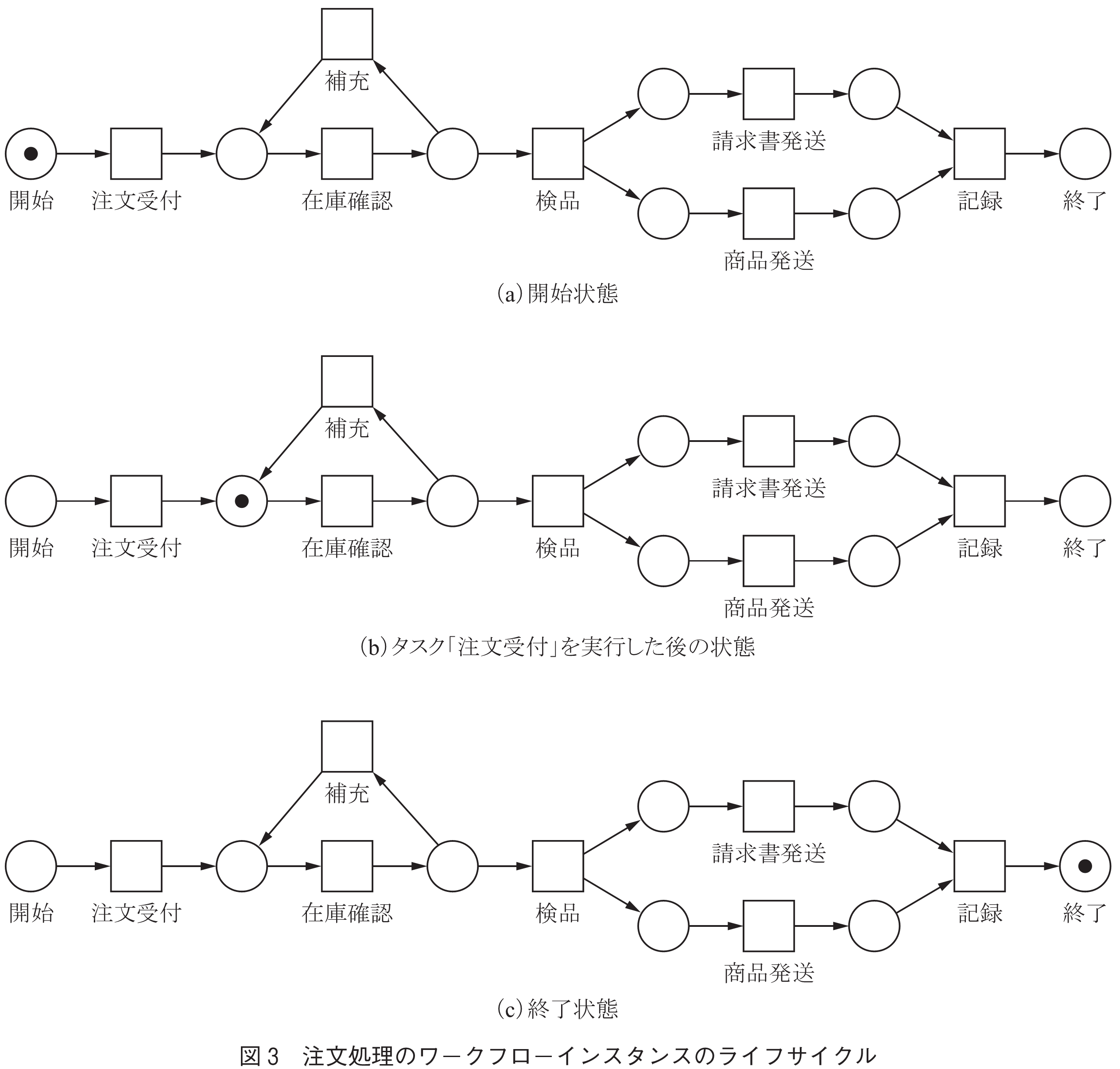
更にペトリネットはトークン(・で描かれる)という要素を持つ.ワークフローのペトリネットモデルでは伝票と思えば分かりやすい.プレースはそこに入るトークンの数によりシステムの局所的な状態を表す.ペトリネット全体のプレースに対するトークンの配置をマーキングと呼び,システムの(大域的な)状態を表す.トランジションは入力側の各プレースに一つ以上トークンがあれば,発火可能であるという.トランジションが発火すると,入力側の各プレースから一つトークンが失われ,出力側の各プレースに一つトークンが加えられる.マーキングと発火によりワークフローインスタンスの状態遷移を表せる.図3は注文処理のワークフローインスタンスの開始から終了に至る状態遷移,すなわちライフサイクルを表す.
市場の変化や法律の改正,技術革新などのビジネス環境の変化は,仕事のやり方を変える.これに適合するようワークフローの定義を変更しなければならない(図4).
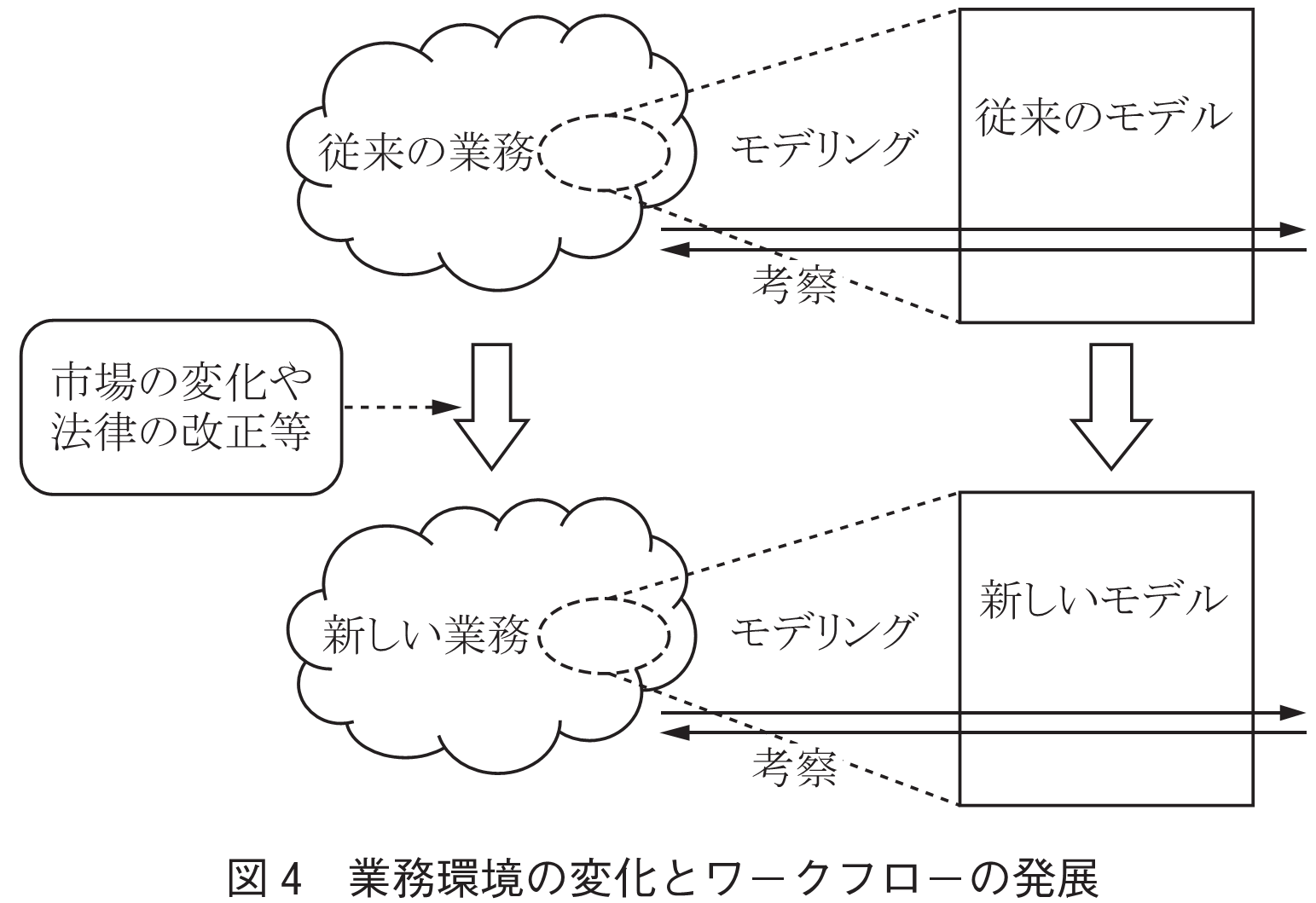
筆者は,この変更をPDCAサイクルと捉えて継続的な改善を促す枠組み(設計・運用・評価・改善)(6),(7)を提案している.設計ステップでは,タスクを洗い出し,それらの順序関係を明らかにした後,ペトリネットでモデリングする.健全性などペトリネットの検証技術は不具合の発見に役立つ.また最近,イベントログからペトリネットを合成するプロセスマイニングの技術(8)も注目を集めている.運用ステップではモデル駆動型アーキテクチャによりワークフローインスタンスを実行並びに監視し,イベントログとして記録する.初期のワークフローでは想定されていない例外も積極的に記録することが肝要である.評価ステップでは運用ステップで得たイベントログにプロセスマイニング技術を適用し,初期のペトリネットと比較することによってギャップを検出する.改善ステップでは評価ステップで得たギャップを取捨選択し,定義に織り込んでいく.
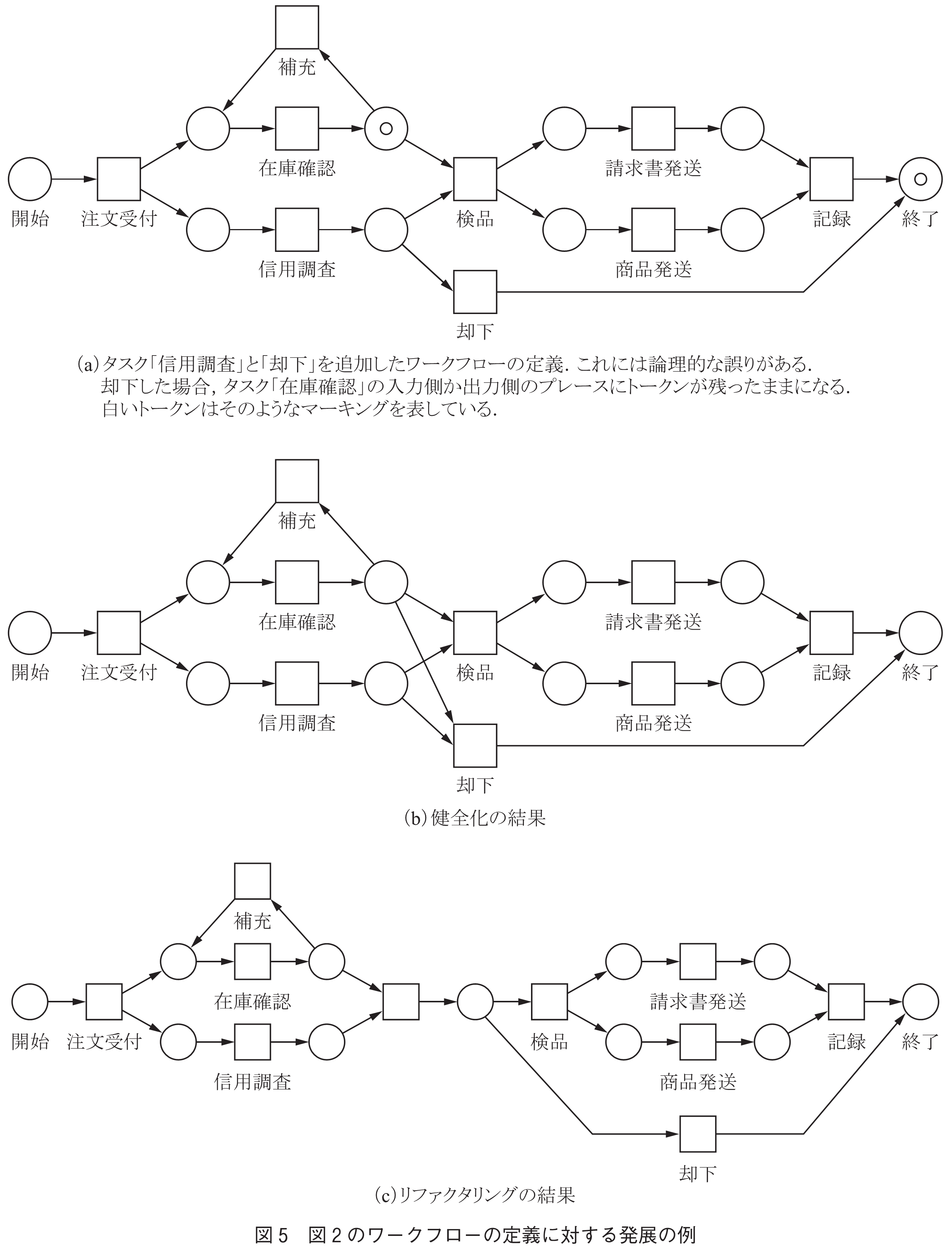
一例として,図2の注文処理のワークフローの定義に対して,タスク「信用調査」と「却下」を追加する場合について考えよう.追加によって得られたワークフローを図5(a)に示す.このワークフローには論理的な誤りがある.信用調査の結果,処理を却下した場合,タスク「在庫確認」の入力側か出力側のプレースにトークンが残ったままになるからである.このワークフローの振舞いを保ちつつ,論理的に正しくなるように修正(健全化(9)という)した結果を図5(b)に示す.更に,この振舞いを保ちつつ,構造を整理した(リファクタリング(10)という)結果を図5(c)に示す.以上のようにワークフローを環境の変化に適合させるための理論を築き上げた.
冒頭で述べたように,数理的アプローチは分野横断的な科学技術として注目を集めており,今後,更に幅広い分野での可能性が期待されている.数理的アプローチのさらなる発展の可能性として三つの方向性を示したい.
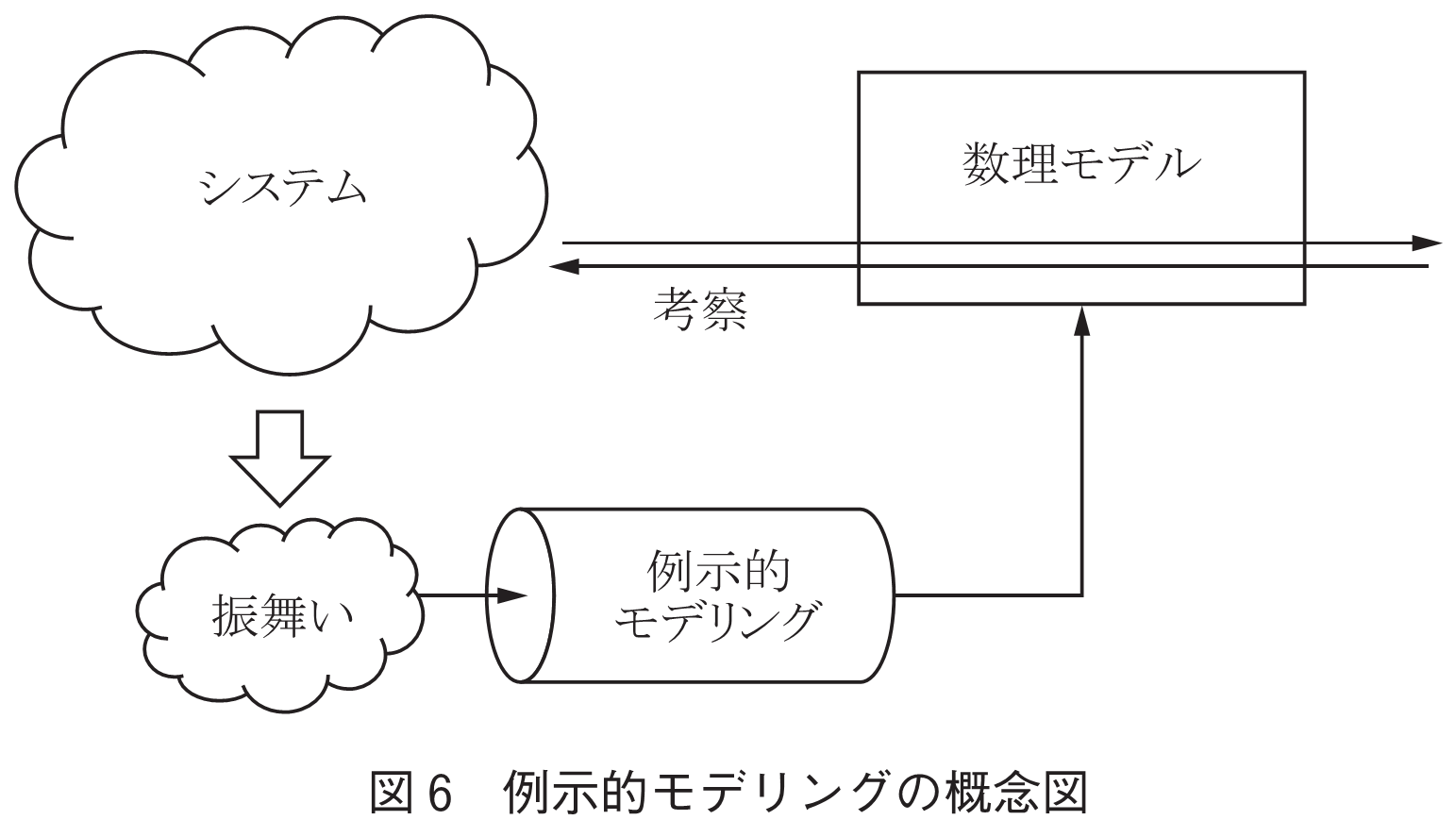
プログラミングのやり方の一つに「例示的プログラミング」がある.私たちが誰かに仕事を教えるとき,「例えば,これをこうして,それから,あれをこうして…」といった具合に具体的な例を使いながら説明することが多い.例示的プログラミングでは,プログラマが処理手順を例示することによってプログラムを記述する.このやり方をモデリングに導入しようとするものが,例示的モデリングである(図6).
プロセスマイニングは例示的モデリングとみなすことができる.システムのイベントログは,プロセスモデルの例示とみなすことができるからである.現状のプロセスマイニング技術は完全ではない.これはプロセスマイニングが,突き詰めれば帰納的推論であり,例外や雑音の存在,イベントの粒度のばらつきなどの影響を受けるからである.これは,プロセスマイニングにおいて,イベントログの品質がプロセスマイニング技術の性能と同じくらい重要であることを意味する.一方,プロセスマイニング技術だけで完全なモデルを得ることは難しいが,モデルの概略を得ることは,実用段階に入っていると考えられる.筆者も複数のモデルから共通部分を抽出するツールとしてプロセスマイニング技術を活用した経験がある.
例示的モデリングの更に進んだやり方として,「例によるモデリング」が考えられる.そこでは入力値と出力値のペアを例示し,入力値から出力値へ変換する数理モデルを推論する.入力値と出力値の範囲が狭ければ,各値を力業でひも付けできる可能性もあるが,通常一般化が不可欠であり,知的な処理が要求される.
将来的には,例示的モデリングのようなコンピュータによるモデリングと人間によるモデリングを組み合わせた方法の出現も予想される.
「群盲象を評す」という寓話がある.複数の盲人が象の一部だけを触って感想を語り合うが,触った部位により感想が異なるというものである.真実の多様性に対する教訓になっている.
モデルはシステムをある側面から切り取ったものである.その側面からは対象を正確に捉えていても,異なる側面は捨象されているかもしれない.また同じ側面であっても異なるスケールのモデルがあるかもしれない.
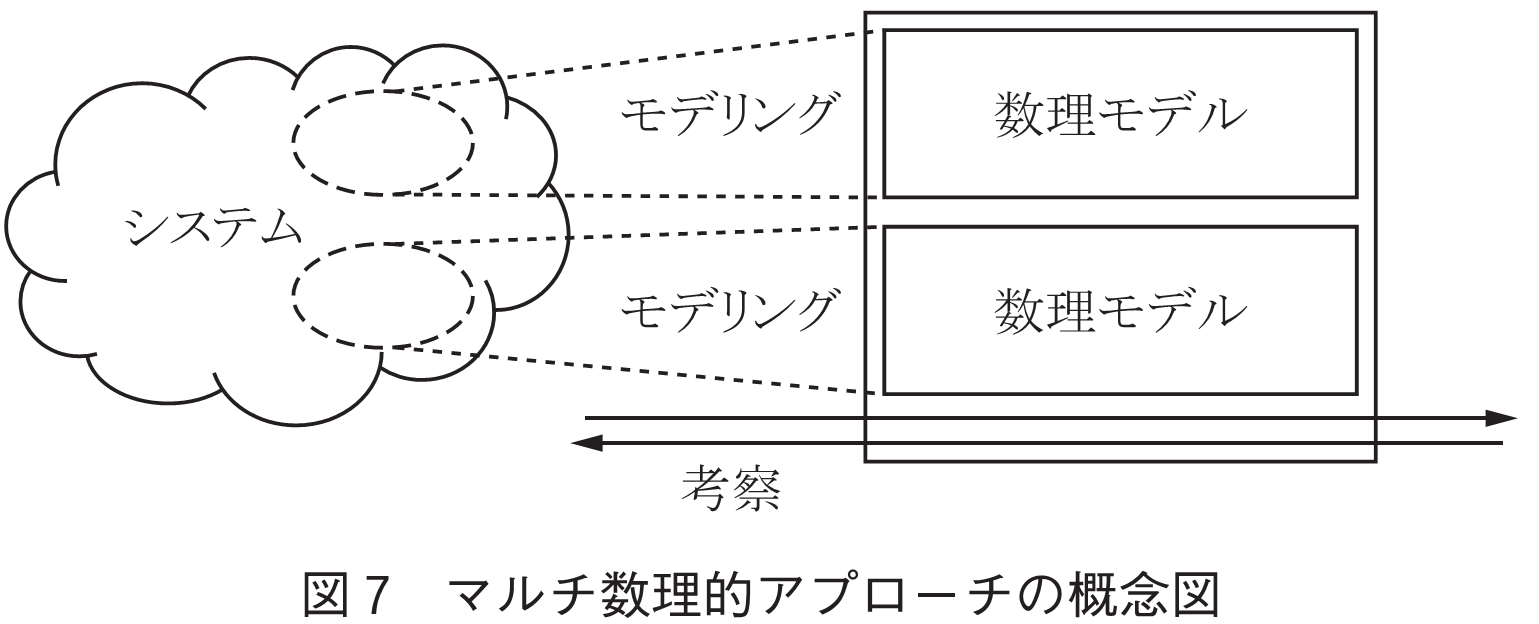
マルチ数理的アプローチとは,システムを多面的に考察すべく複数の数理的アプローチを組み合わせて活用しようとするものである(図7).モデル駆動工学におけるマルチモデリング(10)は有力なアプローチである.マルチモデリングとは,一つのシステムを表現する複数種類のモデルを同時に活用することである.マルチモデリングは,それぞれが固有の類いの知識(構造,振舞い,機能などの側面)と表現を網羅する複数のモデルに基づき協調的な推論を行うことにより,複雑なシステムを管理することを指向する.マルチモデリングではメタモデルを使う.数理モデルでは数学を共通基盤としていることから,モデルの階層化や複数モデルの相互運用などに適していると考えられる.数理モデルのメタモデルの整備や相互運用技術,メタメタモデルの開発が重要な鍵となるであろう.
ところで冒頭の寓話「群盲象を評す」は,合成の誤びゅう(部分的に正しくても,それらを合成した全体は誤ってしまうおそれがあること)に対する教訓にもなっており,マルチ数理的アプローチが挑戦的課題であることも示唆している.
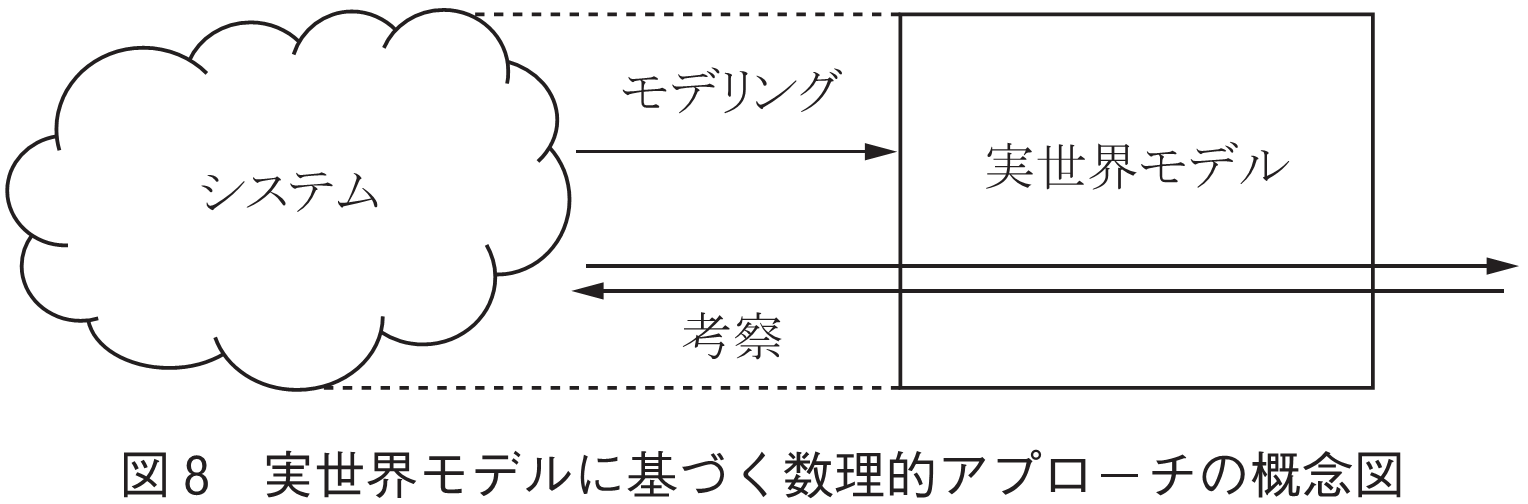
IoT技術の進展により,現実世界のあちこちに配置されたセンサから多種多様なデータが実時間で利用可能になっている.これにより現実世界の姿をより精確に表すモデルが実現可能になってきた.これを「実世界モデル」と呼ぶことにする(図8).なお現実世界は仮想世界と融合し,拡張されることもある.いわゆるサイバーフィジカルシステムも実世界モデルの対象になるであろう.
数理モデルを構築する主要な目的は元来,現象の理解であった.しかし実世界モデルは,ややもすれば十分な捨象が行われず,構築されるきらいがある.実世界モデルはシミュレーションによる現象の振舞いの予測に対して力を発揮する.そもそも現実世界のあらゆる現象に対し,人間が理解できる程度に単純で普遍的な法則が存在するかどうかについても議論が分かれるところであろう.
実世界モデルにおいて大量のデータに埋もれて見えにくくなっている有益な情報を抽出するための技術として,スパースモデリング(11)は極めて有力である.複雑な実世界モデルをリファクタリングする技術や階層化する技術の開発も必要であろう.
本稿では数理的アプローチの概略を筆者の取組みを交えながら紹介した後,更なる発展の可能性として三つの方向性を示した.数理的アプローチの歴史的な経緯と研究動向は文献(12)に詳しく紹介されているので,そちらも併せて参照されたい.数理的アプローチがシステム開発の現場に更に浸透し,活用されることによってイノベーションが加速されることを希望する.
(1) J. Rothenberg, “The Nature of Modeling,” Artificial Intelligence, Simulation, and Modeling, pp.75-92, John Wiley & Sons, 1989.
(2) 山口真悟,葛 崎偉,田中 稔,“ペトリネットによるワークフローのモデル化と解析,”システム/制御/情報,vol.45, no.8, pp.480-489, 2001.
(3) 山口真悟,葛 崎偉,“ネット理論の応用―ワークフローネットとプログラムネット―,”信学FR誌,vol.3, no.3, pp.52-63, Jan 2010.
(4) T. Murata, “Petri nets: Properties, analysis and applications,” Proc. the IEEE, vol.77, no.4, pp.541-580, 1989.
(5) W.M.P. van der Aalst and K. van Hee, Workflow Management: Models, Methods, and Systems, The MIT Press, 2002.
(6) 山口真悟,“ワークフローライフサイクルマネジメントへのペトリネットに基づくアプローチ,”2013信学総大,no.AP-1-4, pp.SS-6-SS-7, March 2013.
(7) 豊嶋伊知郎,山口真悟,“ビジネスプロセスのモデリングツールとしてのワークフローネットとその検証問題,”計測制御,vol.52, no.12, pp.1122-1128, 2013.
(8) S. Yamaguchi and H. Wu, “Protocol inheritance preserving soundizability problem and its polynomial time procedure for acyclic free choice workflow nets,” IEICE Trans. Inf. & Syst., vol.E97-D, no.5, pp.1181-1187, May 2014.
(9) 豊嶋伊知郎,山口真悟,“ペトリネットによるワークフローのリファクタリングとシステム開発における活用の可能性,”信学FR誌,vol.9, no.4, pp.340-349, April 2016.
(10) 日高宗一郎,Jean BÉZIVIN,胡 振江,Frédéric JOUAULT,“(2)メタモデリングとモデル変換(モデル駆動工学の原理と応用),”コンピュータソフトウェア,vol.32, no.2, pp.63-78, 2015.
(11) 岡田真人,五十嵐康彦,中西(大野)義典,永田賢二,“スパースモデリングとデータ駆動科学,”信学誌,vol.99, no.5, pp.370-375, May 2016.
(12) 内平直志,“システム数理と応用,”電子情報通信学会学会100年史,基礎・境界,電子情報通信学会,2017.
(平成28年12月30日受付 平成29年1月30日最終受付)
■ 用 語 解 説
続きを読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード