1．は　じ　め　に

　超伝導もレーザも量子力学でなければ説明できないという意味では量子技術である．しかし，量子力学を使うことによって，情報処理や通信や計測において古典力学よりも本質的に優れた性能を発揮し得るものを，ここでは量子情報技術と呼び，量子暗号，量子コンピュータ，量子計測の現状と将来展望について述べる．本特集の趣旨と，量子情報技術がまだほとんど世に出ていない研究途上の分野であることから，本稿で述べる将来展望は，筆者らの見解であって，必ずしも分野のコンセンサスとは限らないことをお断りしておく．

2．量子暗号の現状と将来展望

　量子暗号は「絶対安全な夢の暗号」として期待されるが，実際は「実用の域にあるが絶対安全と言えない」ものから「課題山積みだが絶対安全が期待される」ものまである．量子暗号は1984年のBB84の提案⁽¹⁾に遡るが，他者の参入が始まったのは，理論は1990年頃から⁽²⁾，実験は1993年頃からである．日本では1995年には論文が書かれ⁽³⁾，以来分野として定着・発展してきた．2000年前後には市販装置を手がけるヴェンチャーが欧米で相次いで設立され，日本でも2010年の東京QKD⁽⁴⁾の現場試験に企業群が参加し，それをNICTの佐々木らが統括した．2012年になると中国でも量子暗号ネットワークの実験が行われ，ロスアラモス研究所では量子暗号を利用した電力系統の制御保護実験を行っている．光ファイバでなく空間伝搬を用いる量子暗号の研究も2000年頃から本格的に始まった．当初の目的は光ファイバの損失制限の打破であったが，次第に衛星間あるいは地上―衛星間量子暗号へ移ってきている．2016年に中国が量子暗号実験衛星を打ち上げたのは記憶に新しい．今年のQuantum 2017ではHuaweiが衛星間量子暗号構想を発表していた．

　こう見ると量子暗号は商用間近に見えるが，目的基礎研究の様相も強い．例えば量子信号は途中で識別再生や増幅により安全でなくなるので，長距離伝送のためには量子中継器が必要となる．これは弱まった信号が雑音に埋もれる前に識別し再生する現行の中継器の量子版で，重ね合わせ状態を壊さないよう「識別せずに再生する」中継器である．また最初の提案であるBB84方式は量子もつれを使わないがE91は使う方式である．これは「ベル不等式が破れているなら安全，そうでなければ安全は保証されない」方式で，基礎研究段階にある．データのみから安全性が確認できるE91は，装置が信頼できない場合に特に必要となる．これを進めたのが「装置無依存量子暗号｣⁽⁵⁾である．

　量子暗号の安全性証明は運用実績を積むことが大事であるが，導入前は理論的な証明しかない．最初は理想的デバイスを仮定する証明に始まり徐々に現実を取り入れた証明に進歩している．日本でも小芦⁽⁶⁾，小柴らの研究が大きく貢献しており，最近若い研究者も多く参入し，日々進歩している．

　実用的な量子暗号の研究に限っても要素技術は目的基礎研究のものが多い．単一光子源はまだ「オンデマンドで確率1できっかり1個」の光子を出すまでに至っていない．単一光子検出器も量子効率が1でかつダークカウントが0のものはない．近年開発されているSSPD⁽⁷⁾やTES⁽⁸⁾などの超伝導光子検出器はダークカウントが少なく，量子効率も高く，ジッタも少なく，通信波長帯（波長1.5µm近辺）にも高い量子効率を有するなどの特徴がある．こうした検出器の重要性を示す例を挙げると，市販の半導体光子検出器ではジッタが大きいので，その時間揺らぎをカバーするよう時間的窓を広げる必要があるが，そうすると雑音を拾うので，本当は量子領域を実現している実験でも，統計的推定の結果古典領域を越えていないという判定になる．しかしジッタの少ないSSPDを使うと窓を狭めてSN比を上げられるので，信頼できる統計的推定ができるようになる⁽⁹⁾．

　以上，光子ベースの量子暗号の話を主体に述べてきたが，現行のコヒーレント光通信に近い方式として，光子でなくコヒーレント状態を用いる量子暗号もある．中でも注目されるのはDPSK（Differential Phase Shift Keying）方式⁽¹⁰⁾，それを「隣同士の光パルスでなくランダムに」位相比較するラウンドロビン方式⁽¹¹⁾，はたまたその改良を図った方式⁽¹²⁾があり，実証実験も行われたが⁽¹³⁾，実用には更なる改良が必要である．同じくコヒーレント状態を用いるもう少し実用的な方法としてデコイ方式と呼ばれる方式もある⁽¹⁴⁾．デコイというのは囮（おとり）の意味で，盗聴者の検知のためのテスト光パルスの強さを複数用意することで検出効率を格段に上げるもので，実際に検証もされている．

　量子暗号の研究開発はいろいろなベクトルを向いており，実用までの距離も様々である．究極の安全性や長距離伝送を追究する目的基礎研究は多様なまま発展するだろう．一方，商用に近い手軽な量子暗号はいずれ淘汰のフェーズに入って行くであろう．実用のためには「標準化」が必要であるが，今はまだその動きが少ない．まずは要素技術の標準化を進め，徐々に方式の標準化に向かう必要がある．今後の量子暗号の研究開発は，高度な方式の多様な追究と実用を目指した標準化の動きの両方が重要となろう．

3．量子情報処理の現状と将来展望

　まず，量子コンピュータの歴史を簡単に述べる．1982年にファインマンが，量子物理系を古典コンピュータでシミュレートすると計算量が爆発する困難を指摘し，それを解決できる万能量子シミュレータとして量子コンピュータの概念に触れた⁽¹⁵⁾．ドイチェが，1985年に計算の量子力学的モデルを示し，万能量子コンピュータを万能チューリングマシンの量子版である量子チューリングマシンとして表し⁽¹⁶⁾，1989年に論理ゲートと論理回路の量子版である量子ゲートと量子回路を導入して表した⁽¹⁷⁾．彼は1992年に，量子コンピュータで古典コンピュータよりも速く解ける問題とアルゴリズムを例示した⁽¹⁸⁾．1993年には，バーンスタインとヴァジラニが量子チューリングマシンの計算量⁽¹⁹⁾，ヤオが量子回路の計算量を研究し⁽²⁰⁾，量子計算量理論の端緒が開かれた．1994年には，ショアが桁数の整数の素因数分解を以下の手間で効率的に解く量子アルゴリズムを考案した⁽²¹⁾が，素因数分解は知られている最良のアルゴリズムである一般数体ふるい法でもの準指数の手間がかかり，その素因数分解の困難性がRSA公開鍵暗号の安全性の根拠であったので，大きな衝撃を与えた．これを契機として量子コンピュータが広く知られるようになり，その実現を目指した研究が様々な物理系で行われるようになった．1996年にはグローヴァーが，ソートされていない個のデータから一つのデータを検索するのに，古典的には回掛かるのを回で済む量子アルゴリズムを考案した⁽²²⁾．

　ここで，量子コンピュータを量子回路モデルで簡単に説明する．量子コンピュータでは，コンピュータのビットに相当する量子ビット（qubit）が情報を担い，それに対して量子ゲートを作用させて計算を行う．量子ビットは物理的にはスピン1/2であり，論理レベルの0と1を表すとの任意の重ね合わせ状態を取ることができる．1量子ビットの量子ゲートとしては，例えば，古典的なNOTに相当するXゲートや，ゲートなどがある．量子回路で頻繁に現れるアダマールゲートは，に作用するとと重ね合わせを作る．これらの演算子は，物理的にはスピンの回転を表す．また，2-qubitの代表的な量子ゲートである制御NOTゲートはで表され，1-qubit目がのときのみ2-qubit目をNOTする．

　量子ビットに重ね合わせの状態を許すと，量子並列性が生じる．-qubitが初期状態にあるとして，全てのqubitにを作用させると，となり，-bitの全ての数の重ね合わせの状態ができる．ユニタリ変換がからを計算するタスクをとすると，によって個のについて並列的にの計算が行われ，手間は一つのと変わらない．しかし，の確率振幅はであり，確率でしか結果を読み出せないので，それだけでは計算は速くならない．ここでが周期関数の場合には，の方にFFTの量子版である量子フーリエ変換（QFT)⁽¹⁸⁾を適用すると，干渉効果で周期が抽出できる．これがショアのアルゴリズム⁽²¹⁾の原理である．このように，干渉効果によって，正解の確率振幅は足し合わされ，不正解の確率振幅は打ち消し合うようにするのが，量子アルゴリズムであり⁽¹⁸⁾，そのためには重ね合わせの位相が保たれていなければならない．

　量子ビットの重ね合わせの位相は，環境との相互作用によって容易に破壊されてしまう．このデコヒーレンスが，量子コンピュータを実現する上で最大の障害となることは，当初から予想されており，ショアのアルゴリズム提案後すぐに量子誤り訂正符号のアイデアが出された⁽²³⁾．古典的な誤り訂正と本質的に異なるところは，量子状態は複製できないこと，観測するとかに収縮してしまい重ね合わせの情報が失われること，量子誤りはビットフリップと位相フリップ及びそれらが同時に起こることを解決しなければならないことである．古典的な線形符号を組み合わせてX基底とZ基底で誤り訂正を行うが，符号化された量子情報は観測せずに，誤りのシンドロームのみを観測することによって量子誤りが訂正可能であることが示された．例えば，1-qubitを7-qubitに符号化することによって1-qubitの量子誤りから守ることができる．更に，1997年には，量子誤り訂正過程を含む全ての量子演算に誤差を許しても，誤差があるしきい値以下であれば，信頼性の高い量子計算が行われる誤り耐性量子計算の概念によって，大規模量子計算の可能性が示された⁽²⁴⁾．ここまでの教科書として文献(25)を挙げておく．当初のしきい値は0.001%程度と悲観的な値であったが，2007年にラッセンドルフが，Kitaevのトポロジカル量子計算⁽²⁶⁾から，二次元的に配列したqubitで最隣接間の量子演算だけを用いた表面符号に基づき0.75%のしきい値を持つ方式を考案し⁽²⁷⁾，実現の可能性が現実味を帯びてきた．

　本稿を執筆している2017年春の時点で，量子コンピュータをめぐる状況は大きく動いている⁽²⁸⁾．現時点で，量子コンピュータのハードウェアとして最も進んでいるのは超伝導量子ビットである．主な研究拠点は，米国ではUCSB/Google，IBM，Yale大，Rigetti，欧州ではオランダのDelft工科大，日本では東大／理研／NECなどである．最近ではIBMが2017年3月に，産業界初の万能量子計算システムIBM Qの商用化を目指すと発表し，2～3年以内に50-qubitを目標にすることを明らかにした．IBMは，既に5-qubitの超伝導量子コンピュータをクラウド経由で公開していたが，5月には16-qubitに更新した．Googleは，後で述べるD-Waveから512-qubitのマシンを買っていたが，その後2014年の秋にUCSBのMartinisグループを自前の量子コンピュータを作るために雇った⁽²⁸⁾．Googleは今年中に50-qubitの超伝導量子コンピュータを作って，スーパコンピュータに対する量子優越性⁽²⁹⁾を達成する計画のようである⁽²⁸⁾．このように，現在，超伝導量子コンピュータのトップグループは50-qubit^(注1)を目指してしのぎを削っている．C. Rigettiは，Yale大で7年，IBMで3年超伝導量子ビットの研究に携わった後，2013年に独立して起業し，既に70億円の投資を集めた．量子コンピュータへの投資という点で，先鞭をつけたのはD-Waveであり，1,000万円の出資金で1999年に起業し，総額180億円の投資を集めた．量子コンピュータの開発には，途方もないリソースとエフォートが必要だが，その中には大きなブレークスルーをもたらす天才的なアイデアが必要な部分と，人海戦術で膨大なリソースを投入すれば解決できる部分があり，ばく大な投資が集められれば後者は確実に加速し，前者の天才的人材も集められるかもしれない．しかし，超伝導量子ビットをここまで育て上げたのは，地道な基礎研究であった．

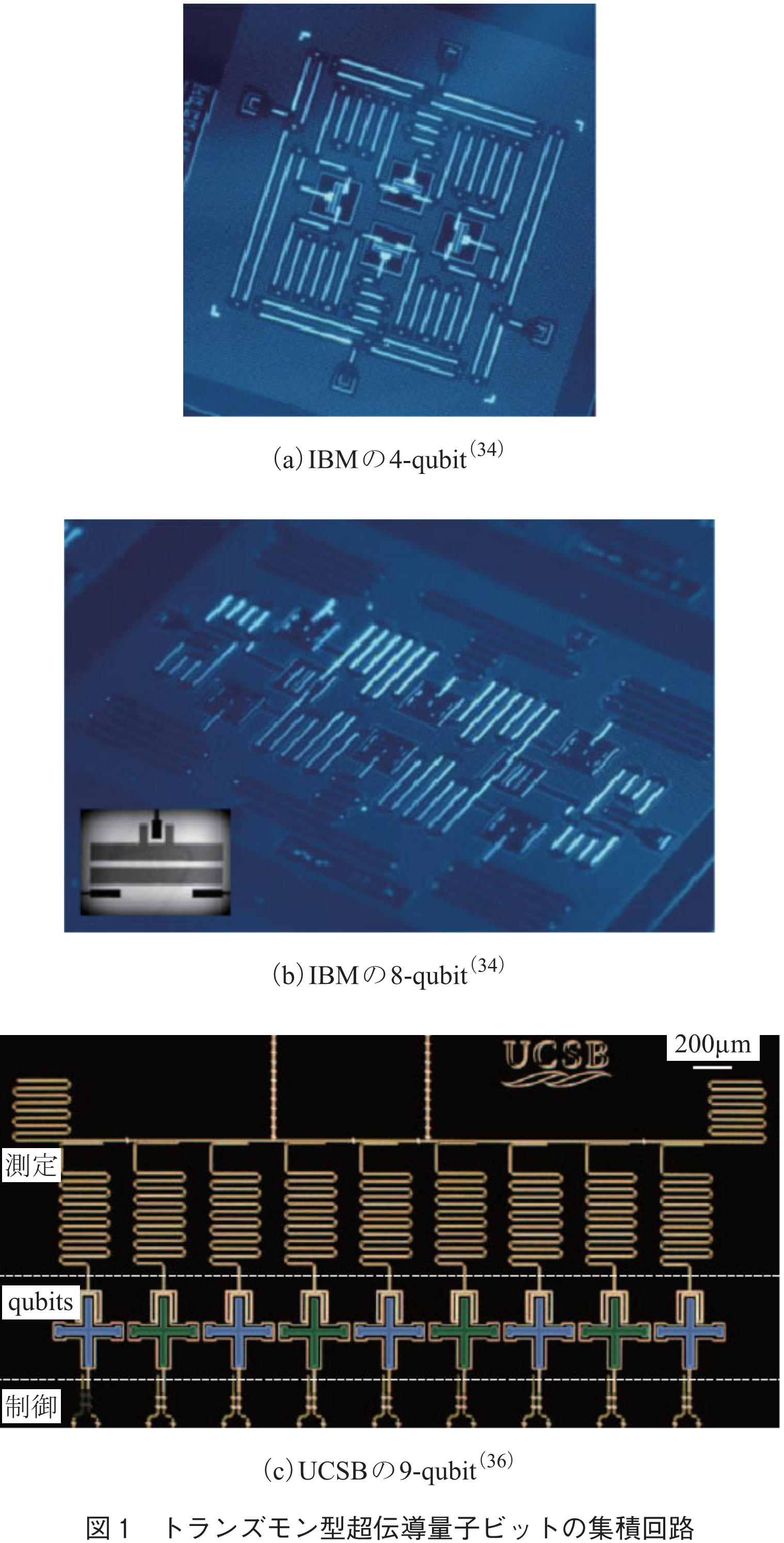
　1999年に世界で初めて超伝導量子ビットを実現したのは，NEC基礎研究所の中村，Tsaiらであり，Cooper Pair Boxの電荷の状態を量子ビットとしたものであった⁽³⁰⁾が，コヒーレンス時間は1nsしかなかった．超伝導では，電荷のほかに，磁束，位相などの状態を量子ビットとして用いることができ，回路や材料の改良とともに，コヒーレンス時間の大幅な改善がなされてきた^(31),(32)．現時点で最もコヒーレンス時間が長いのは2007年にYale大が考案したトランズモン（transmon）型⁽³³⁾であり，当時1µsを実現した．これは，Cooper Pair Boxを大きな静電容量でシャントして非線形振動子にしたもので，下から二つの準位を量子ビットとして用いる．電荷エネルギーよりもジョセフソンエネルギーの方が支配的で，電荷揺らぎの影響を受け難いため，非常に長いコヒーレンス時間を示す．その後もトランズモン型量子ビットは改良され続けて，コヒーレンス時間は100µsまで伸びている⁽³⁴⁾．現在，主要グループの超伝導量子ビットはほとんどトランズモン型である（図1）．量子演算の精度も向上し，2014年に表面符号による誤り耐性しきい値⁽²⁷⁾以下の誤差が達成された⁽³⁵⁾．表面符号を意識した二次元の実験⁽³⁴⁾や一次元の9-qubit実験⁽³⁶⁾も行われている．誤り耐性を確保するには多数の量子ビットを二次元的に配列し，最近接qubit間の量子演算で表面符号を実装する必要があるが，当面は50-qubit程度までの実装が目標であろう．中国も超伝導量子ビットで急速に実力を付けてきており，最近10-qubitのエンタングルメントを報告している⁽³⁷⁾．

　量子ビットの規模として超伝導とほぼ並んでいるのが，イオントラップであり，メリーランド大のモンローのグループは，5-qubitで任意の量子回路を組み，小規模なアルゴリズムを実行している⁽³⁸⁾．モンローは2015年にIonQを起業している⁽²⁸⁾．Microsoft Station Qは，まだ全くの未知数であるが物理的に頑強な量子ビットになると期待されるマヨラナ粒子を用いたトポロジカル量子計算⁽²⁶⁾に絞って，Delft工科大などとコンソーシアムを組んで研究を行っている⁽²⁸⁾．半導体では原子レベルのドーピングや量子ドットを用いた方式が提案され，日，欧，豪などで実験されているが，詳細は最近の解説^(32),(39)を参照されたい．

　現在，量子コンピュータが注目されているもう一つの理由は，D-Waveが2,000-qubitの量子コンピュータを既に市販し，しかも，NP困難な組合せ最適化問題を速く解くと喧伝していることである⁽⁴⁰⁾．このD-Waveマシンは，超伝導量子ビットを2,000個集積化してはいるが，量子ゲートは実装されておらず，門脇・西森の量子アニーリング⁽⁴⁰⁾をハードウェア的に実行する専用機である．組合せ最適化問題を，イジングモデルという古典スピンの多体系のエネルギーを最小化して基底状態を求める問題にマップすることができ，それを解く方法の一つが量子アニーリングである．問題はスピン間の相互作用を表すとしてプログラムされる．我が国で開発されたコヒーレントイジングマシンは，光パラメトリック発振器のポンピングを発振しきい値に下から近付けてゆくと最も損失の小さいモードで発振するという原理に基づいてを最小化し，2,000ノードの実験が行われている⁽⁴¹⁾．これらは，最小化しようとしているをアナログ量として実現しているため，本質的にアナログ計算機であり，NP困難な問題に答えを出しても計算量理論に反しないが，不可避な誤差によってどこまでスケールするか不明である．

　ファインマンが想起した量子シミュレーション⁽¹⁵⁾は，ディジタル量子コンピュータではソフトウェア的に実現される．現時点では比較的制御性の高い量子系である光格子中の中性原子やイオントラップを用いたアナログ量子シミュレーションの実験が盛んに行われている⁽⁴²⁾．これはパラメータが比較的自在に変えられる量子物理実験であり，ハバードモデルによる高温超伝導の機構解明などが期待されている．これが，新しい電子材料の開発につながることを期待したい．

4．量子計測の現状と将来展望

　量子計測のうち本会に最も関係が深い時間標準・周波数標準では，香取が2001年に提案した光格子時計⁽⁴³⁾が10^－18の精度を実現し，現在の秒の標準であるセシウム原子時計の10^－16を既に二桁凌駕している．秒の二次表現に採用され，次の秒の標準の有力候補となっている．光格子時計の精度は，一般相対論に基づく重力による時間の遅れを介して標高差をセンチメートル精度で計測できることを意味しており，測地や資源探索への応用も期待される⁽⁴⁴⁾．光格子時計の原理を簡単に説明する．ドップラーシフトを避けるために，原子は極低温に冷却されて，強いポテンシャル中に閉じ込められていなければならない．しかし，一つの原子が出す信号は量子不確定性のためにSN比が悪く，多数回繰り返し測定しなければ精度が出ない．光格子時計では，レーザで三次元的な干渉じま（光格子）を作り，電界の腹に原子をトラップすることによって，一度に個の原子の信号を見ることで，SN比は1個の場合の倍に向上する．原子をトラップするための光格子の強力な電界によって，原子のエネルギー準位がシフトし，遷移周波数が電界に依存して変わってしまうと標準として使えないが，時計遷移の両方の準位に対するシフトが等しくなる波長（魔法波長）が存在することに香取は気付き，それが光格子時計の誕生へとつながった．

　光格子時計の原子数による精度向上は，量子力学的にはスピン1/2を個集めて同じ状態にしたスピンのコヒーレントスピン状態の量子不確定性がとなる標準量子限界に相当する．個のスピンの間にエンタングルメントを作れば，量子不確定性を真の量子限界（ハイゼンベルク限界）まで減らせる可能性があり⁽⁴⁵⁾，この原理が量子計測に実用的な恩恵をもたらすことを期待したい．

5．お　わ　り　に

　大規模な量子コンピュータの実現は非常に挑戦的な目標であるが，科学と工学のフロンティアであることは間違いなく，アポロ計画のようにその過程で多くの科学的，技術的な副産物を生み出すことが期待される．欧米は官民ともにばく大な研究投資を始めており⁽²⁸⁾，量子情報に特化した研究センターや研究プログラムで人材育成も行われている．

　超伝導量子ビットに限らず量子ビット系の課題は，集積化であろう⁽³⁴⁾．量子ビットをたくさん並べて，それらの間を量子的な媒体でつないで演算する方式で集積度を上げるには，マイクロ波技術や材料，半導体で培われた集積技術などを駆使する必要がある．そういう意味で，量子コンピュータの開発には，本会の様々な分野の専門家が貢献できる可能性がある．2016年秋にはERATO中村巨視的量子機械プロジェクトが始まり，超伝導量子コンピュータの研究に我が国でも大きな期待がかかっている．本格的な量子コンピュータ実現への道はまだまだ入口の段階であり，将来的にどの物理系が大規模化を実現するかはまだ分からない⁽²⁸⁾．欧米中並の研究投資を人材育成まで含めて長期的視野で行えば，我が国にも十分チャンスはあるはずである．

　量子コンピュータは素因数分解しかできないという誤解があるが，素因数分解は古典コンピュータよりも量子コンピュータが強力であることの強い傍証の一つにすぎない．それ以外にも，量子シミュレーションや量子化学計算⁽⁴⁶⁾には大きな期待があるし，機械学習に使える可能性もある⁽⁴⁷⁾．まだ存在もしない量子コンピュータのアルゴリズムを考えたのはほんの一握りの研究者であったが，既に目の前に16-qubitの量子コンピュータがあって誰でもインターネットからアクセスでき，近々50-qubitの量子コンピュータが実現するとすれば，話は違ってくる．これからは誰でも量子アルゴリズムの研究ができる．新しい画期的な量子アルゴリズムが生み出されることを期待したい．

文　　　　　献