1．は　じ　め　に

　図1のように平面上に点と直線で描かれたグラフを考えよう．直線を棒材，点を接合部と考えることでこれらのグラフをフレームワーク（枠組み，リンケージ）として捉えることができる．そのようなフレームワークは，頂点の辺の本数やつなぎ方，頂点配置に応じて異なる力学的性質を有する．本稿では主に，静力学的性質つまりフレームワークの剛性を中心に話を進める．

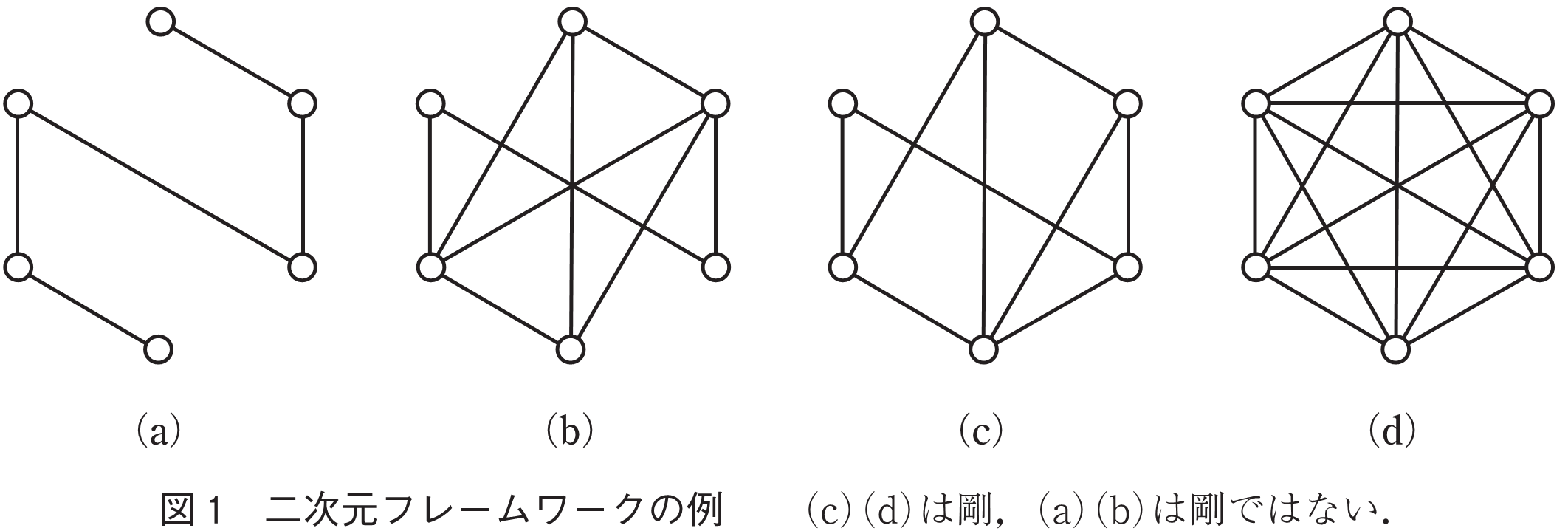
　我々は経験的に，棒と点のつながり方，つまりフレームワークのグラフがその力学的性質に重要な役割を果たしていることを理解している．図1(a)のような頂点数に比べ辺の本数が少ない場合，フレームワークは辺長を変えることなく様々な変形が可能である．一方，図1(d)のような完全グラフでは動きに自由度のない安定的な状態と考えられる．しかしながら，図1(b)(c)のように頂点数と辺数が同じ場合であってもその剛性は異なることがあり，剛性とグラフの関係を正確に理解することは容易ではないように思われる．面白いことに，平面においては，ある種の一般性の仮定の下において，剛性とグラフの組合せ的構造の関係が完全に理解されており，ある補助2部グラフ上でのマッチング問題を複数回計算することによって剛性判定という幾何的問題を組合せ的に解くことが可能である．本稿では，このような組合せ的アプローチに焦点を絞り，その代表的成果を紹介する．