1．は　じ　め　に

　複比（ふくひ：Cross Ratio）は直線上や平面上に与えられた四つの点の座標から引き算と割り算で算出される無次元量である．数学由来の概念だが実は電気回路と深く関係する⁽¹⁾．しかるに振り返って高校の学習要綱を見ると理系クラスであっても複比が含まれない．

　本稿では初心に立ち戻り，二次元平面上の4点を用いて複比を定義する．直線点列，三角形，四角形などの基本図形と数式を照らし合わせることで，4点の位置に応じた複比の振舞いに慣れ親しみ直感力を育むことを狙う．更に，高校の範囲を超えるが，少し発展させて，複比が波動の反射率という物理的意味を持つことにも触れる．

2．引き算と割り算の共演

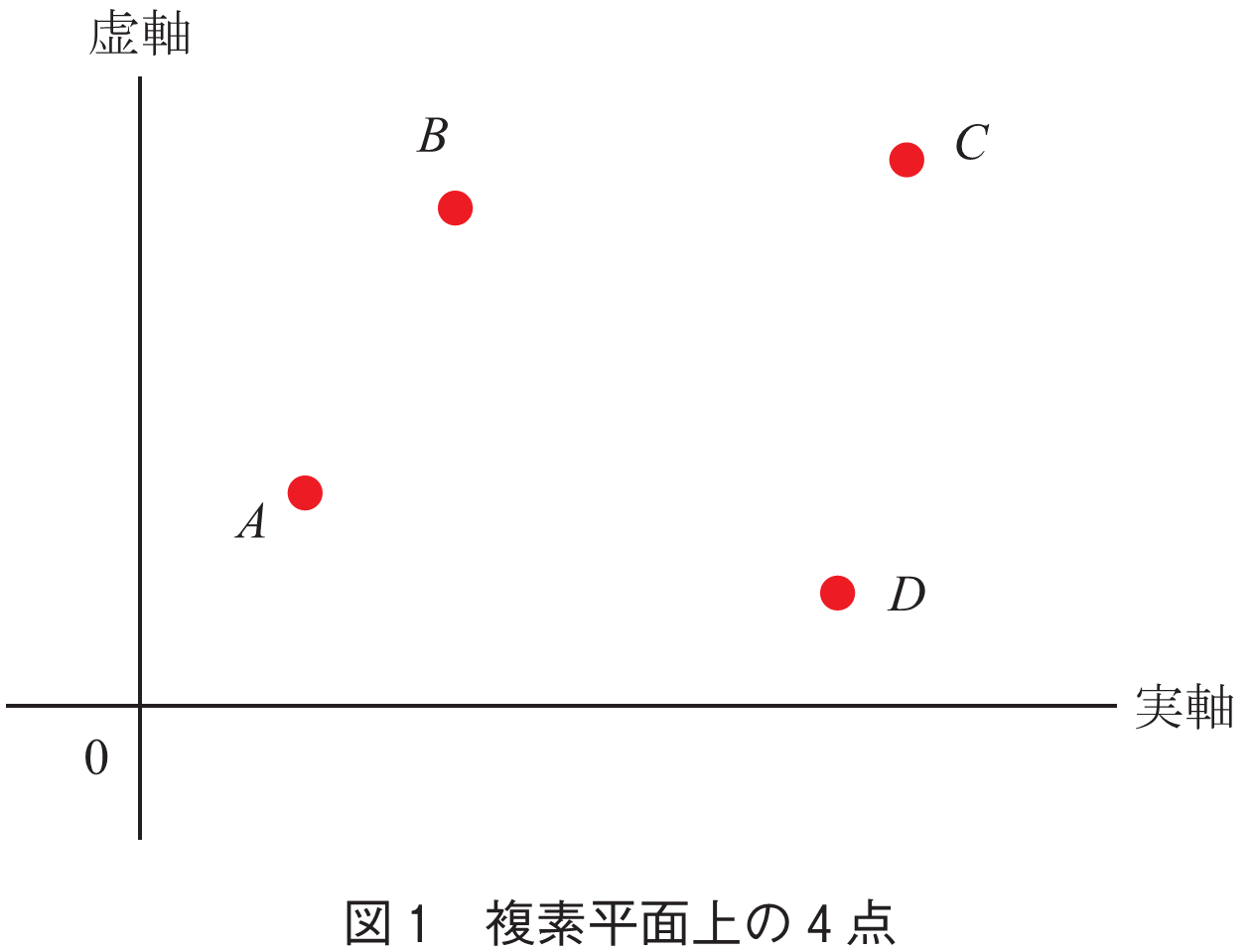
　複素平面上の任意の位置に点を四つ与える．ただしこれらは互いに異なる位置にあるとする．プロットした例を図1に示す．各点，，，は実軸と虚軸をベースとする直交座標で決まる複素数に対応する．ゆえにこれらの間で四則演算が可能である．

　本稿では4点の複比をギリシャ文字（ロー）を用いて

と定義する．複比は引き算と割り算が美しく共演する「差の比の比」である．あるいは分母を逆数化することで割り算を掛け算的に表示できることも式(１)で分かる．

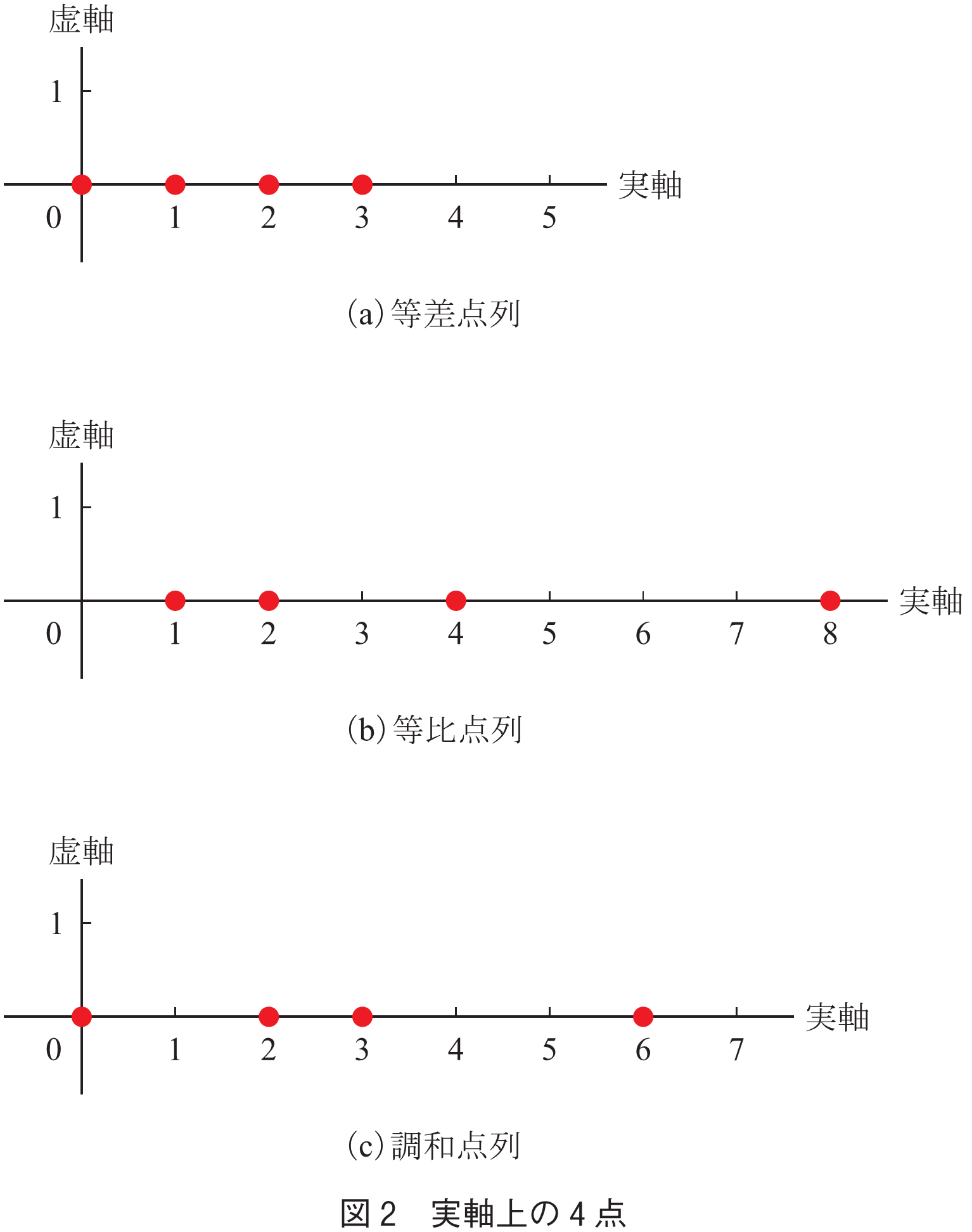
　複比は変数を四つも含むので一見煩雑に思えるかもしれない．でも安心してほしい．式中で四つが規則正しく巡回的に並んでいるのでが思いのほか美しく振る舞うからだ．以下の章で具体例に触れる．