1．周期構造中の電磁界とは

　周期構造は基本単位の構造を周期的に並べて形成したものであり，自然界に数多く見られる．例えば固体を原子スケールまで拡大すると，原子，分子，イオンなどが規則正しく配列された結晶という周期構造になっている．またモルフォ蝶が青い金属的な光沢を放つのは，その鱗粉が樹状突起を林立させた形の周期構造を持ち，特定の波長を持つ光のみを反射するためである．このような特性を模倣し，電磁波や光を用途に応じて人工的に制御できる構造を探索する研究が続いている．その電磁界の特徴は，周期構造を含む内外領域における波長が局所空間的に変調されているということである．これにより偏波や周波数の選択，ビーム形成などの有用な特性がもたらされる．

　周期構造の例を図1に掲げる．このうち（a）から（f）が一次元，（g）と（h）が二次元，（i）が三次元の周期構造である．媒質に周期性を導入する方法は，次の［P1］～［P3］のように大別できるが，複合させる場合もある．

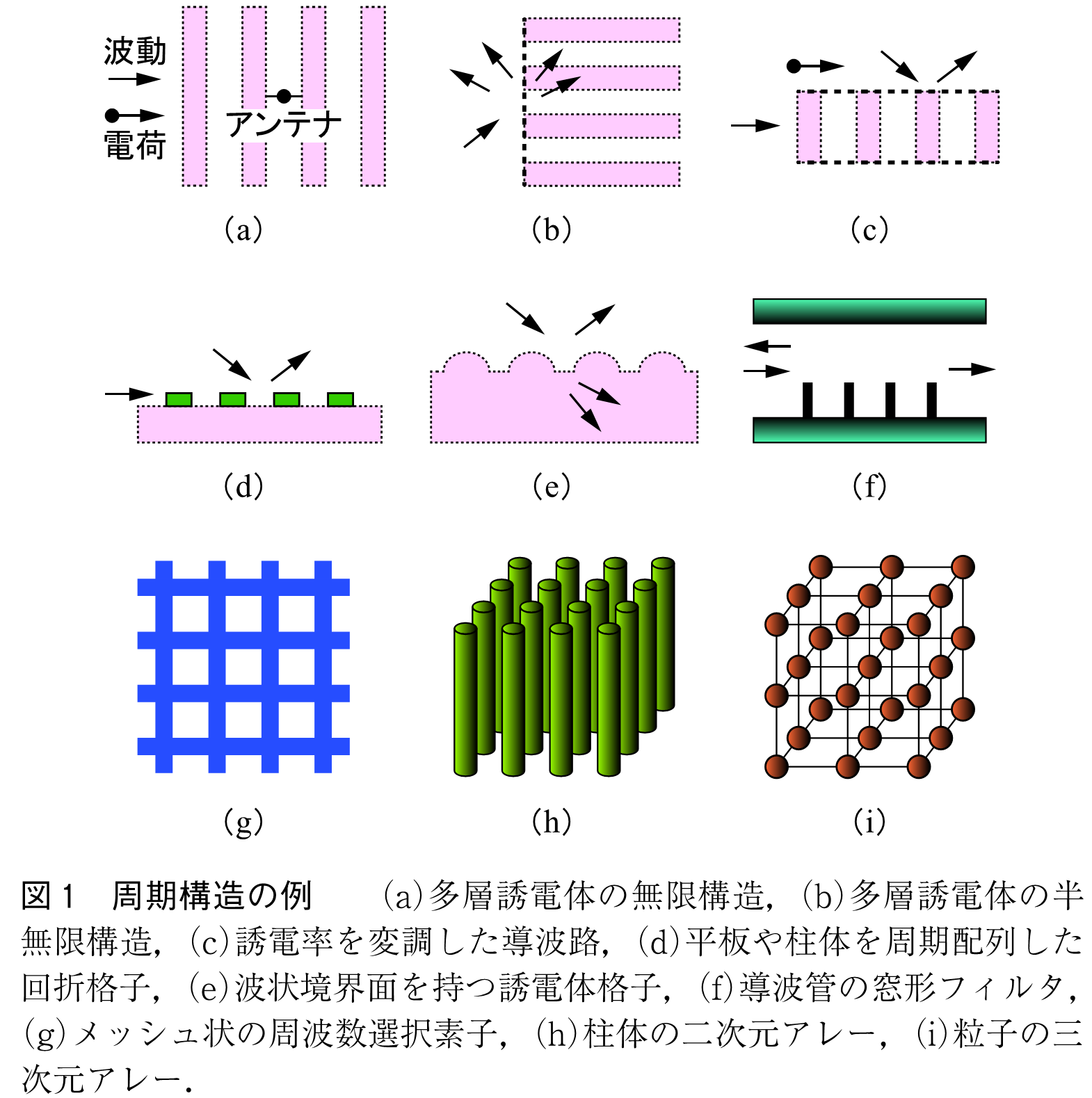
 ［P1］空間内で媒質定数すなわち誘電率，透磁率，導電率を周期的に変化させる．

 ［P2］粒子，媒質素子などの単体または有限集合を基本単位として，これを周期的に配置する．

 ［P3］媒質の表面形状，または異種媒質間の境界形状を周期的に変形させる．

　周期構造中の電磁界は，その媒質の特性に基づき，基本単位領域内の界を繰り返したものとなる．ただし完全に同一の反復ではなく，隣り合う単位周期間の対応する2点における界の複素値の間には，一定の位相差がある．ここでは位相定数，は周期である．この性質を記述したものが，2．で述べるフロケ（Floquet）の定理⁽¹⁾であり，これが周期条件を与える．すなわち基本単位領域内の界が分かれば，全空間内の界が求められたことになる．

2．周期構造に対する電磁界解析

　周期構造に対する電磁界解析とは，マクスウェル（Maxwell）方程式の一般解の中から，境界条件と周期条件を満たす特殊解を選択することである．周期条件に含まれる位相定数の値としては，構造自体が持つ固有値を用いる場合と，外部からの励振の状況により定められる値を用いる場合とがある．

　なお，周期構造中の電磁界を表す関数は，量子力学や固体物理学に現れる電子の波動関数との類似性を持つ．すなわち両者とも空間座標に関する2階微分を含む波動方程式に支配される．この微分方程式とは，電磁気学ではマクスウェル方程式から導かれるヘルムホルツ（Helmholtz）方程式であり，量子力学ではシュレーディンガー（Schrödinger）方程式である．また前者における媒質の波数と，後者における結晶のポテンシャルは，共に空間座標に関する周期関数で与えられ，波動方程式内の対応する箇所に現れる．この類似性により，前者におけるフロケの定理と周波数は，後者ではそれぞれブロッホ（Bloch）の定理とポテンシャルに対応する．

　構造の周期性と波動の伝搬方向を方向に限定して，フロケの定理を述べておく．波動は方程式

を満たす．波数すなわち媒質定数がのように周期を持つとき，定数の値ごとに定められる周期関数を用いて，式（１）の解が

と表されることがその定理である．

3．周期構造における電磁界の問題の分類

　電磁界の議論においては，次の［Q1］～［Q3］のように問題を分類できる．これらを複合したものもある．図2は図1（a），（c），（e）をモデルとして語句等を追加したものである．

 ［Q1］構造中にいかなる形で電磁界が存在できるか．

 ［Q2］構造中にいかにして電磁界を導入するか．

 ［Q3］構造内に周期的な波源があるとき，構造外にいかなる電磁界ができるか．

 ［Q1］は固有振動を検討するものであり，数学的には同次問題である．偏波や周波数に関して，構造に対応した特定の条件が満たされれば，外部からのエネルギーの供給がなくても，若しくは初期的に僅かな外力を加えるだけで振動が継続し，電磁波が固有モードとして伝搬する．この波は結晶格子理論ではブロッホ波として知られている．振動が減衰しない（減衰する）周波数帯域を，フィルタ特性の用語に準じて通過域（阻止域）と呼ぶ．

 ［Q2］は周期構造内に固有モードを励振する問題であり，手段としては，①他の導波路や給電線との接続による導波，②電子ビームとのエネルギー結合，③平面波入射などがある．①では入射端での反射損を抑制するために整合器などが必要となる．③では固有モードの伝搬定数に整合するように平面波の入射角を調整する．なお，励振された固有モードは媒質の不均一性による部分反射が干渉し，位相が整合するブラッグ（Bragg）波長では全反射となる．この特性は分布反射器として動的単一モード（DSM : Dynamic Single Mode）レーザなどに応用されている．

 ［Q3］は外部からの励振に対する応答を決定する散乱・回折問題であり，数学的には非同次問題となる．媒質が電磁波により照射されると，誘起された電磁流が二次波源となって外部空間に電磁波を放射する．媒質が周期構造を持つとき，定数の位相差を持つ波源が基本単位構造ごとに並ぶため，離散的な角度方向に放射ビームすなわち格子モードが形成される．これは二次波源の代わりに一次波源としてアンテナアレーを置いた場合と同じ効果である．

4．一次元多層構造における固有モード

　周期構造の特徴である周波数選択特性と遅波特性を表す数値例を，図2［Q1］の多層構造を例として掲げておく．図3右上に示すように，層と層を交互に重ねた構造において，層の誘電率を，透磁率を（真空中の値）とする．成分（, ）を持つ電磁波が方向に伝搬するものとし，時間因子の下で，層内の電界成分を，式（１）の形の波動方程式の基本解を重ね合せて

と表す．ここで，は媒質の波数，は未定の定数である．磁界成分は式（３）にマクスウェル方程式を適用して求められる．固有モードの位相定数をとすれば，フロケの定理により，電磁界は周期条件を満たす．この条件と境界面における界成分の連続条件とを連立させる．得られた同次連立一次方程式が非自明な解を持つための条件，すなわち固有値方程式が次のように得られる．

ここで記号は媒質の波動アドミタンスを用いてのように定義される．

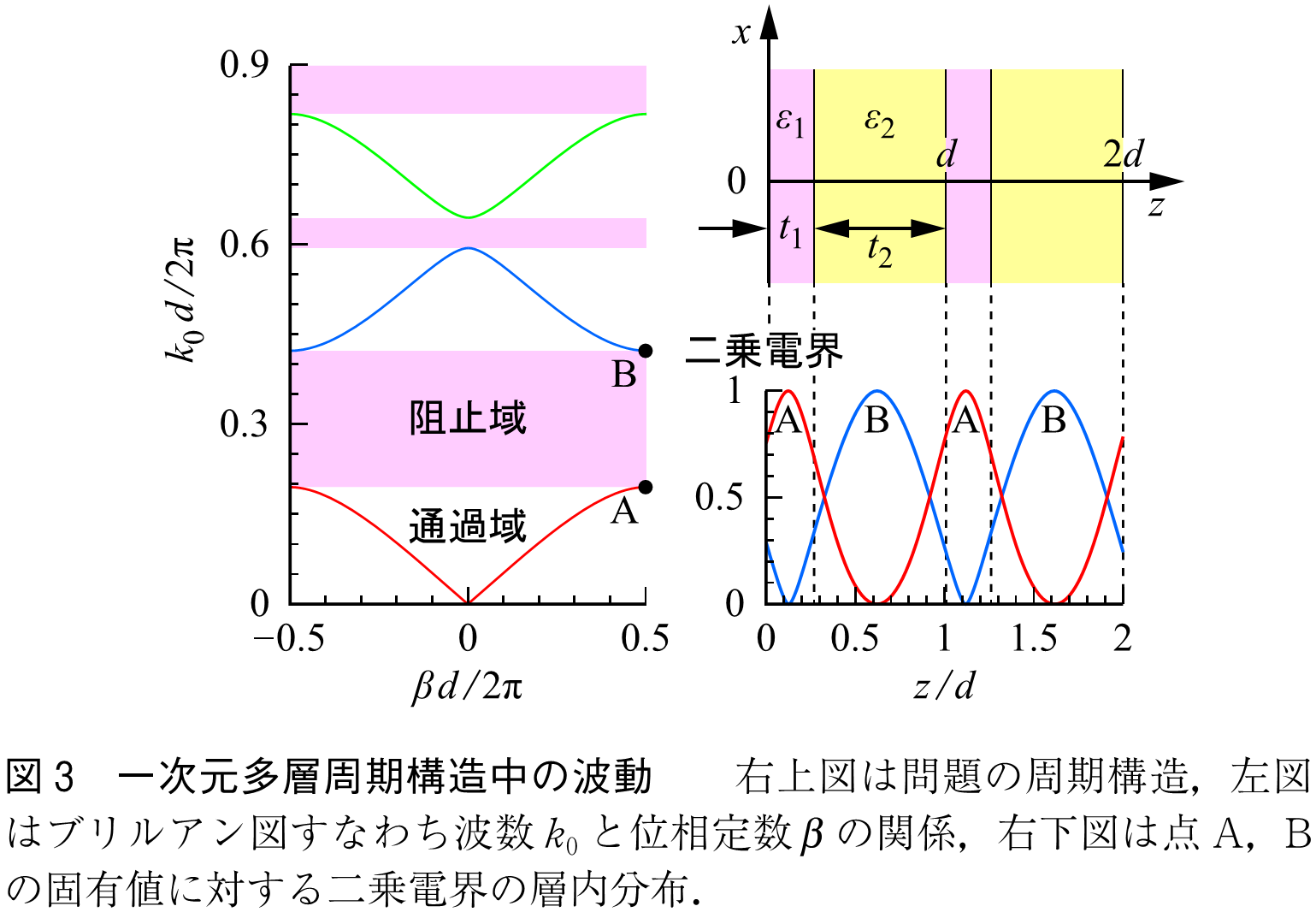
　図3左には式（４）の解，すなわち位相定数と波数（はそれぞれ真空中の誘電率，同じく光速，周波数）との関係を描いた．この図はブリルアン図（Brillouin Diagram），エネルギーバンド図，図などと呼ばれる．パラメータは，，，である．グラフ軸は無次元となるように正規化しており，縦軸は正規化周波数である．周波数の増加とともに，周期構造中の固有モードが存在する通過域と存在しない阻止域とが交互に形成される．阻止域は光工学の分野ではフォトニックバンドギャップ⁽²⁾と呼ばれる．通過域の端にある点A，Bにおける（, ）の値に対して，構造内に分布する二乗電界を最大値で正規化して図3右下に示した．電界のピークは，点A，Bに対してそれぞれ誘電体層内，真空層内で起こる．このとき隣り合う単位周期の間で，界の振幅は同一分布であるが，から位相は反転する．また，曲線の傾きで与えられる群速度は，導波管の場合と同様に，周期構造においてもエネルギーや狭帯域信号の伝送速度を表す⁽¹⁾．この速度は（原点を除く）及びにおける固有モードでは零になる．

5．むすび

　周期構造中の電磁界の探求は19世紀末期のレイリー（Rayleigh）の研究まで遡り，20世紀中期までの成果はブリルアンの著書⁽³⁾にまとめられた．当時の人口誘電体，フィルタ，遅波素子などに関する研究内容については，文献（１）第9章の参考文献を参照されたい．近年ではフォトニック結晶⁽²⁾，メタマテリアル⁽⁴⁾，能動性素子などを含む広範な構造に研究が展開され，本分野への注目はますます高まっている．

文　　　　　献

（2024年10月21日受付）