
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|
小特集 4.
完全準同形暗号の最近の研究動向
Recent Research Topics on Fully Homomorphic Encryption
abstract
暗号化状態のままであらゆるデータ演算を可能とする完全準同形暗号技術に対する期待は大きい.従来の完全準同形暗号の構成法は主に二つの原理へと分類されるが,動作時間など効率面の抜本的改善や運用上の問題の軽減のため,従来とは異なる原理に基づく完全準同形暗号の実現に向けた研究も進められている.それらの研究は残念ながらいまだ成功に至っていないものの,今後の研究の進展を祈念する意味も込めて,本稿ではそうした新たな完全準同形暗号の構成原理に関する研究動向について概説する.
キーワード:完全準同形暗号,ブートストラップ,符号,非可換群
本会誌では,用語は①文部省(文部科学省)学術用語集電気工学編,②本会編の改訂電子情報通信用語辞典,③本会編のエンサイクロペディアハンドブック,用字は④文化庁編の公用文の書き表し方の基準,に基づき統一している.
本稿中の「準同形」は,上記②に従っており,著者の原稿では「準同型」が用いられていたが,ここでは本会方針に基づき掲載した.
(本小特集の別の記事でも既に述べられているであろうが,)公開鍵暗号化技術の一種である(注1)準同形暗号(homomorphic encryption)は,単にデータを暗号化して秘匿するだけにとどまらず,「暗号化のままデータ(平文)に演算を施せる」とでも表現すべき追加機能を有する.より詳しくは,この暗号化方式の平文の集合を,暗号文の集合を
として,平文集合
上に何らかの演算(例えば
で表す)が定義されている状況を考える.このとき,演算
に対応する何らかの演算(例えば
で表す)が暗号文集合
上に定義され,暗号文
について関係式
(1)
が成り立つとき,(演算に関する)準同形暗号と呼ぶ.ただし,Decは復号アルゴリズムを表し,秘密鍵(復号鍵)の表記は割愛している.また,暗号文の演算
を,演算
に関する準同形演算と呼ぶことが多い.
集合と演算の組及び
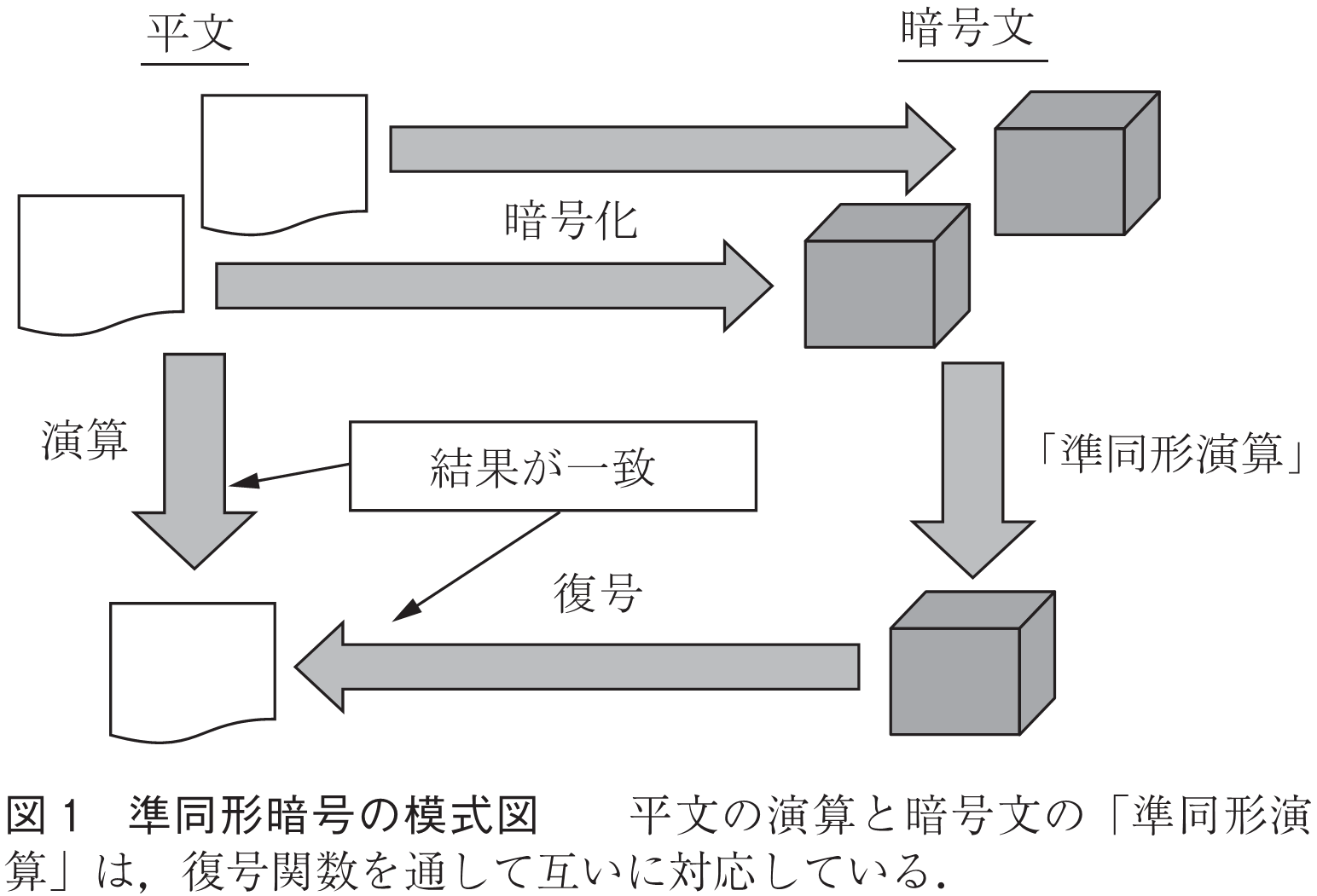
をそれぞれある種の代数系とみなすならば,式(1)は復号関数Decが数学的な意味でこれらの代数系の間の準同形写像として働くことを意味する(図1).「準同形暗号」という名称のゆえんであろう.RSA暗号やPaillier暗号(1)は準同形暗号の例であるが,前者では平文に対する乗法,後者では平文に対する加法という具合に,平文について単一の演算のみが考慮されている.
続きを読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
「電子情報通信学会 - IEICE会誌」アプリをダウンロード