
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

情報通信技術の急速な発展に伴い,我々を取り巻く環境においても,アンケート形式で行われるような母集団の中からある一部だけを抽出して調査する標本調査や科学的な調査に加え,インターネットやセンサなどの機器を活用して多種多様なデータが比較的容易に入手できるようになってきた.
標本調査ではターゲットの母集団を定め,母集団のどの構成要素もサンプルとして選ばれる可能性が等しい(機会の平等)ような標本抽出が前提になっている.そのための有効な方法が無作為抽出法である.しかし,実際は,回収率が低く無回答によるバイアス(選択バイアス(selection bias)の一種)や,回答はあったものの幾つかの項目に無回答(欠測値データ,欠損値データ,missing data)であることから生じるバイアスの問題がある.これらはその後の統計解析を複雑にし,複雑な分析方法をとったとしても無視できないバイアスが生じることも多い.
科学的な調査を行うには,ある特徴を持つ構成要素が選ばれにくいまたは回答しないといった状況を作ってはいけない.この意味で,機会均等性を無視して標本サイズを大きくするというアプローチは誤りである.調査しやすい構成要素が選ばれやすいということが容易に起こる.歴史的には米国大統領選挙で200万の調査が予測を外し
3,000の調査が当選者を当てたという例もある(1).
インターネット調査では,調査のWebページにアクセスできる任意の人を対象とする調査もあるが,多くは,何らかの対価を支払うことを条件に事前に調査に協力できる対象者をプールした人工母集団を作っておき,その集団を調査対象として調査することが行われる.人工母集団は,目的に応じた本来の母集団(e.g., 有権者全体,大学生全体)と,性別,年齢層,職業など属性変数を整合させるなどの工夫が見られる.この方法は,標本調査論で言う割当法(用語)と呼ばれるものと近い.この方法の欠点は,例えば,男性・50歳代・商工業地区在住を満たす有権者50名を抽出することになったとき,該当者の集団から標本を無作為抽出することが極めて困難であることである.割当法による標本調査は成功例もあるものの失敗もあり,近年では余り用いられない.
最近は,様々なセンサや機器が開発され莫大なデータがオンラインで瞬時に得られる.これらによるデータは,データ入力などの作業が不必要で,瞬時に分析可能なデータとなることも魅力的である.また,医療の分野でも電子カルテ化が進んでいる(注1).企業では,膨大な売上げデータや社員の健康管理データもある.このようなセンサなどで自動収集できるデータと個人や企業のデータやその解析結果を個人/企業へフィードバックする場合はよいかもしれないが,ある集団に対する知見を得たい場合は,データが得られたプロセスを注視し,サンプルが母集団をどの程度代表するかを常に意識・検討しておかなければならない.
近年の標本代表性を軽視し大標本が強調される調査の方法は,ともすれば,先に述べた大統領選挙予測の時代(1930年代)へ退行したという指摘も聞く.しかし,筆者は,インターネット調査や現在のビッグデータの利活用は大いに進めるべきであると考えている.データ収集と分析の即時性は大きな魅力であるし,先に述べたセンサの発展によって今まで採取できなかったデータが取れるようになったことも重要な発展である.また,とりあえずはざっくりとした結果であるが速報性が有用といったこともある.本稿でお伝えしたいことは,情報技術の利活用によるデータ収集と解析においても,少なくとも伝統的な統計学の果実である選択バイアスの議論や欠測値データ解析の理論と方法を念頭に置いておくべきではないかということである.
選択バイアスとは,調査に参加する個人やグループといった対象(調査対象)を選ぶ際に生じる誤差である.調査対象を得た段階で,それが母集団を代表しない場合,結果が有効でなくなるため,この誤差に起因する推定量のバイアスを言う.
ある母集団において母平均を知りたいとし,その母集団から無作為にサイズ
の標本
をとる.つまり,
(1)
このとき,標本平均はの一致推定量(用語)となる.
では,が
に依存しているとき,標本が偏って選ばれたとすれば何が起こるだろうか.確率変数
を,
が選ばれる(観測される)とき
,選ばれないとき
と定義する.選択バイアスが生じる状況とは,式(1)は母集団からの無作為標本ではなく,
が与えられた下での
の条件付き分布を持つ母集団からの標本となる.
このとき,データの標本平均は
に確率収束し,一般に
であり母平均の一致推定量にならない(注2).
例えば,大学から離れたところに実家がある大学受験生がアパート探しをする状況を考える.近年,不動産業界は競争がし烈であるため,A不動産は合格発表前にアパートの先行予約を受け付け,不合格になった場合は無料でキャンセルに応じるというキャンペーンをやっている.A不動産が持つデータによる大学合学率は受験生全体の合格率を上回る.つまり,合格率の推定値としてはバイアスがあるのである.その理由は,先行予約する受験生は一般に自信・実力があるからである(注3).つまり,A不動産の持つデータは自信のある受験生を選択的に選んだことになっており選択バイアスが生じているからである.大学に合格(不合格)のとき,A不動産で先行予約する(しない)とき
とすると,一般に
と考えられ,
と
は独立ではないのである.
さて,と
との関係を表す量として以下を定義する.
このとき
は,母平均の一致推定量になる.選ばれた標本だけの単純な平均値はまずいが,
の逆数に比例した重みを付けた推定量を用いなければならないということである.つまり,選ばれにくい個体にはより重い重みを付与するということであり,この考え方は重要である.この方法を用いるためには,事前に
と
を見積もっておかなければならない.
標本が当初想定した形で得られないとき,欠測(missing)があると言う.まず,直接観測された変数(観測変数)が一次元の場合の欠測値問題を考える.
ここで,に欠測が生じ得るとし,
が観測されるとき
,欠測するとき
とする.ここでは選択バイアスはないものとし,
は母集団からの無作為標本とする.
この母集団からの無作為標本の設定は2.の選択バイアスと酷似する.存在するデータのみに基づいて推測を行うことは,のデータを使うということであり,選択バイアスの場合と同一である.違いは,ここでは,標本サイズ
が分かっており
のデータがあることから,
をデータから推定できることである.
次に観測変数(ベクトル)が二次元である場合を考える.以下の無作為標本を考える.
ここで,欠測はにのみ生じ得るとし,
が観測されるとき
,欠測するとき
とする.
は常に観測されるとする.
に関するこの条件は本質的でなく一般的な状況は後ほど考える.欠測があるとき,
の母平均
がどのように正しく(または誤って)推定されるのか考えよう.
,
と置く(注4).
存在する(欠測のない完全データ)のみを用いて推測を行う方法をリストワイズ削除(listwise deletion)または完全ケース解析(complete-case analysis)と言う.すなわち
によってを推定することになる.これは先に述べたように,
の一致推定量ではなく,適用してはいけない方法であることが分かっている.
そこで,Inverse Probability Weighting Estimator(IPWE)という推定量が提案されている.
ここで,
(2)
である.式(2)は傾向スコア(propensity score(2))若しくは,欠測メカニズム(missing-data mechanism)と呼ばれている.
母集団の分布が正規分布などで仮定できるパラメトリックモデルが利用可能な場合は,最尤法(用語)が適用できる.
としよう.ここでと
は既知の関数で,
と
が未知母数である.観測ベクトルの順番を入れ換えて
とする.ここで,は欠測を表す.このとき,尤度
を最大化する母数の値を最尤推定量とする.
最尤法を適用するには欠測メカニズムの項が面倒である.そこで,
(3)
が仮定できると,簡略化された尤度
に基づく最尤推定量が一致性を有することが示される.仮定(3)を欠測メカニズムがMAR(Missing At Random)であるという.
文献(3)に倣うと,欠測メカニズムには三つのパターンがある.観測が想定されている全変数をと書き,
の欠測メカニズムを
とする.
を
に従って観測される部分
と欠測部分
に分ける.つまり,
の1の成分に対応する
の成分を集めた確率変数の集合が
である.なお,
である.このとき
・ 欠測メカニズムがMCAR(Missing Completely At Random):
(4)
・ 欠測メカニズムがMAR:
(5)
・ 欠測メカニズムがNMAR(Not Missing At Random; or MNAR):
(6)
式(3)がMARを示すことを確かめておこう.MARの定義式(5)は欠測パターンごとに確認する.観測がのとき,
であり,(5)は
となる.この式の成立は自明.観測がのとき,
であり,定義式(5)は
となる.この式が(3)である.
次章では,大量欠測を伴う大規模データの分析方法を紹介する.
大規模データの解析では計算量と計算精度が重要であり,計算機科学の観点からも様々な発展がある.大規模データの特徴としてデータサイズ(volume),即時性(velocity),非等質性(variety)がうたわれるが,そこに,大規模ゆえの欠測を指摘したい.確かに,優秀なセンサやログ記録をネットワークによって蓄積していく大規模データにおいては欠測は発生しないかもしれない.しかし,例えば,販売記録データでは,ポイントカード等の導入によって購買者の個人情報を利用可能としたID-POSデータが有用であるが,意図的に個人情報を提供したくない(すなわちカードを持ちたくない)購買者も少なからず存在し,彼らについては個人情報が欠測となり,その欠測はランダムとは言えないだろう.先に述べたように,近年Webアンケートによる質問紙調査が盛んである.本稿では,対象母集団が不明確で選択バイアスの可能性があるというWeb調査の根源的な問題は横に置き,設問の幾つかのみを選択回答するという意味で生じる欠測値問題を取り上げ,その統計分析方法を論じる.
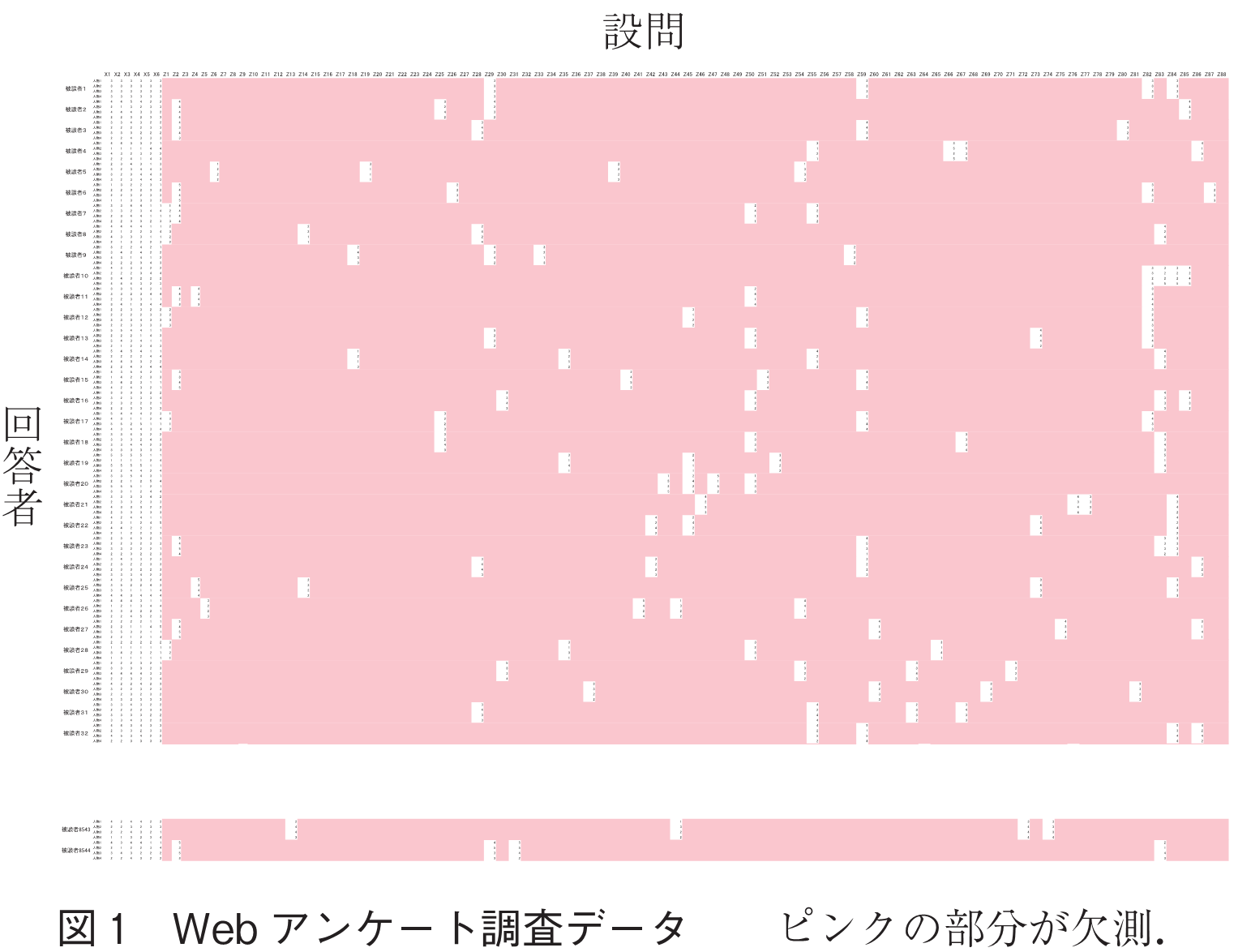
人を評価する軸は様々である.ある評価者は勤勉さが重要と考えるかもしれないが,別の評価者は勤勉さには興味がなく社交性が大事と考えるかもしれない.勤勉さに興味のない評価者には勤勉さを問う価値はなく,興味のない質問項目は,欠測となるかランダムに選ばれた回答が得られるにすぎない.そこで,こういった状況では,数多くの評価項目を用意し,評価者に興味のある項目を選択回答させる方法が考えられる.ところが,このような調査デザインは調査後の統計分析が困難であるため実際に採用されることはほとんどなかったと思われる.このように,回答者が項目を選択しなかったという行為によってデータが欠測する場合,状況によっては大量の欠測が生じる.図1のデータは,実験協力者に人物刺激を与え第一印象を評定させたもので,94項目が用意されている.94項目の中で6項目は必答で,他の88項目はその中から4項目を選択回答させている(4).なお,人物刺激は4種(4名)であり回答者はである(調査期日:2011年12月28日~2012年1月10日).このデザインの場合,データの約90%が欠測する.このような場合の統計的推測の方法及び推定値を効率的に求める計算アルゴリズムは容易ではない.ここでは,Hiroseほか(5)と狩野ほか(6)によって提案された方法を紹介する.
本稿では,データの大半が欠測している場合の因子分析(用語)モデルの推定問題を扱う.ここで紹介する方法は他の統計モデルでも適用できるであろう.次元の観測変数ベクトル
に対して
個の潜在共通因子ベクトル
を持つ因子分析モデルは
と書くことができる(e.g.,文献(7),(8)).詳細は省くが,因子分析ではまず,因子数の選定と因子負荷量
の推定を行う.欠測指標変数のベクトルを
とする.
は,回答者が質問項目
を選択し回答することを示す.観測変数が
個の場合,欠測パターンの総数は
である.
個から必ず
個を選択する場合,その数は
である.先に示した調査デザインでは,
であり,欠測パターンの数は
となる.
回答者がを選択するとき,
へは真っ当な評価を行うと仮定し,すなわち,因子分析モデルが正しいとする.一方,
を選択しないときは,もし強制的に回答させられたとすれば無作為に選択肢を選ぶ等,その分布は想定した因子分析モデルに従わないと考える.そういった反応を表す確率変数を
とする.このとき,観測変数
の分布は
と表現できる.ここで,次の仮定を置く.
このとき,欠測メカニズムを含めたfull-likelihoodは
となる.ここで,は
番目の回答者が選択し回答した質問項目から成る観測ベクトルであり,
と
は
の平均ベクトルと分散共分散行列である.この尤度は,MARの下で適用される直接尤度(用語)(direct-likelihood or observed likelihood)と同等である(注5).
直接尤度の最適化には,擬似ニュートン法や,共通因子と欠測値を潜在変数とみなしたEMアルゴリズム(用語),(9),(10)などが用いられてきた.しかしながら,これらの手法は1970~80年代のサンプルサイズがそれほど大きくなかった頃に確立された手法であり,現在Webで取得されるような「サンプルサイズが膨大,観測変数の数が多い,欠測率90%が大きい」データに対しては,計算時間が非常に掛かり現実的でない.そこで,文献(5)では,共通因子のみを潜在変数とみなしたEMアルゴリズムを導出した.
提案したアルゴリズムのパフォーマンスを数値実験によって検討した.提案したアルゴリズムは,従来のEMアルゴリズムよりも数百倍程度計算速度が速いことが分かった.データの大半が欠測している場合,一般に大きなサンプルが必要となる.大量欠測時における推定精度とサンプルサイズの関係を調べたところ,90%の欠測の状況では数万程度の大きさの標本が望ましいことが分かった.(参考情報:90変数の場合,5,000人程度あれば5%以下の誤差で分析可能.)提案手法は,初対面第一印象データに適用し,対人認知構造を探ったり(11),職場の人間関係予測(12)に応用した.
データ分析を行う上で,データの欠測は無視できない.これからデータ分析を行う本稿の読者には,ここで述べた伝統的な統計手法を念頭に置き,データに欠測があった場合でも,安易に欠測のあるレコードを削除するのではなく,まず欠測の状態確認してほしい.どの変数の値がどれくらいの量,欠測しているかの状態にもよるが,欠測メカニズムを仮定することで分析できることがある.完全ケース解析の場合も,母集団に対して非常に少量のレコードを削除する場合はそれほど気にする必要はないが,大量のレコードを削除する場合はバイアスを考えてほしい.レコード削除によって,結果的に標本が偏って選ばれてしまうかもしれない.
本稿をきっかけとして,電子情報通信分野でしばしば発生するデータの欠測の問題を,統計学の研究者とのコラボレーションによって解決することで,今後の技術の進歩につながることを期待したい.
(1) 鈴木督久,佐藤 寧,アンケート調査の計画・分析入門,日科技連,2012.
(2) P.R. Rosenbaum and D.B. Rubin, “The central role of the propensity score in observational studies for causal effects,” Biometrika, vol.70, no.1. pp.41-55, April 1983.
(3) R. Little and D. Rubin, “Statistical Analysis with Missing Data,” vol.4, Wiley, 1987.
(4) 廣瀬 慧,金 順暎,狩野 裕,今田美幸,松尾真人,“大量欠測データに対する因子分析モデルの最尤推定,”2013年度統計関連学会連合大会,p.164, Sept. 2013.
(5) K. Hirose, S. Kim, Y. Kano, M. Imada, M. Yoshida, and M. Matsuo, “Full information maximum likelihood estimation in factor analysis with a large number of missing values,” J. Stat. Comput. Simul., vol.86, no.1, pp.91-104, 2016.
(6) 狩野 裕,廣瀬 慧,今田美幸,松尾真人,“大量欠損データの探索的因子分析:大規模Webアンケートデータの統計解析,”日本行動計量学会第42回大会発表論文抄録集,vol.42, pp.138-139, Sept. 2014.
(7) 柳井晴夫,前川真一,繁枡算男,市川雅教,因子分析―その理論と方法,朝倉書店,1990.
(8) 市川雅教,因子分析,朝倉書店,2010.
(9) D.B. Rubin and D.T. Thayer, “EM algorithms for ML factor analysis,” Psychometrika, vol.47, no.1, pp.69-76, March 1982.
(10) D.B. Rubin and C. Liu, “Maximum likelihood estimation of factor analysis using the ECME algorithm with complete and incomplete data,” Statistica Sinica, vol.8, pp.729-747, 1998.
(11) 金 順暎,廣瀬 慧,今田美幸,吉田 学,松尾真人,藤井竜也,“個人属性が対人認知構造に及ぼす影響について―Webアンケートによる大規模調査の解析結果から,”信学技報,HCS2012-13, HIP2012-13, pp.97-102, May 2012.
(12) M. Imada, K. Hirose, M. Yoshida, S. Kim, N. Toyozumi, G. Lopez, and Y. Kano, “An interpersonal sentiment quantification method applied to work relationship prediction,” NTT Technical Review, vol.15, no.3, 2017.
(平成29年6月6日受付)
■ 用 語 解 説
(注1) 日本の特徴として,国民皆保険制度や介護保険制度の下,活用できるデータが豊富にあることが指摘できる.このような貴重なデータを,プライバシー問題を考慮しつつどのようにしてオープン化を図るかが喫緊の課題である.
(注2) もちろんと
が独立であれば一致推定量になるが,一般には
と
は関係する.
(注3) たとえ無料であっても,記念受験組は決して先行予約しない.
(注4) は集合
に含まれる要素の数を表す.
(注5) なお,ここでの欠測はNMARである.
続きを読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード