1.1　マス・フォア・インダストリ研究所の設置

　筆者が所属する九州大学マス・フォア・インダストリ研究所（IMI）は2011年に設立された．2013年には，京都大学数理解析研究所に次いで，我が国2番目の大学附置の数学研究所として文部科学省共同研究・共同利用拠点に認定され，活発な研究活動を行っている．設立目的は，欧米等で特に進む，数学の産業応用への展開及びそれに資する博士人材育成，そして学問としての数学へのフィードバックである．

　数学へのフィードバックとは，新しい数学研究領域の発見・開拓・体系化である．IMI設立は，計算機性能向上が生んだ社会全般での数理的課題の急速な増加に対して，全面的・本格的に数学が参入しなければ，未来の数学がやせ細ってしまうのではないかという反省からでもあった．

1.2　ものづくりを支えた工学者の応用数学力

　よく知られているかどうかは別にして，我が国における大学工学部，特に機械や電気・電子専攻の教員たちには，海外に行けば応用数学者と呼ばれるような優れた数学研究を，工学からの必要に応じ実践されている方が多くいた．しかし，年代で言えばせいぜい団塊の世代までである．かつて計算機性能が貧弱であった頃，課題を自らが数学的に追い詰めなければ，期待する成果が得にくかったことが理由である．しかし，計算機性能が向上してくるにつれ，徐々に，そのような必要を感じることが少なくなったのであろう．工学者の数学への関心が薄れてしまった．以前は，極めて高いレベルの応用数学を開拓する工学者がいて，その下でかなり数学に強い人材が育っていった．その結果，企業の技術開発現場においてしばしば現れる現象の解明や背後にある数理的課題の解決にも対応できる態勢ができていた．また数学に強い物理系出身者が，その後も産業界で数理的課題の解決に貢献した例も数多い．これらの人材が，日本のものづくりを世界一級のものにする一翼を担ったことは疑いない^(1),(2)．

1.3　皮肉な現象

　ところが歴史は皮肉な方向に進んだ．先に述べた工学系での応用数学の展開が，いつからか，理学系の数学教室における研究や教育に，純粋数学への極端な偏りをもたらすことになったのである．役立つことなど度外視して，美しい数学のみに重点を置こう．もちろん，“既に数学になっているもの”からも新しい研究が生まれている．また，重要な未解決問題も多い．その解決への努力を通じて，今も，新たな研究対象が生まれ多様で重要な研究が続いている．これらが人類の文化の発展に寄与することは間違いない．しかも，たとえその研究に没頭する数学者が認識しなくとも，将来の産業に大きなインパクトを与え得ることは確かである．情報セキュリティと言えば，現在その8割以上を担うのはRSA暗号だ⁽³⁾．1977年のその発明には，ギリシアで発見された素数の無限性と素因数分解の一意性定理から，およそ2500年の時を要したのである．

2.1　20世紀抽象数学の応用が始まった

　大学1，2年生で学ぶ数学の多くは，現在も微分積分と線形代数など19世紀のものである．20世紀になり物理学からも離れて発達した代数幾何，整数論，トポロジーや表現論などは，数学科以外では通常は学ぶ機会がない．これらの数学では抽象的議論が多くなされるが，具体例も豊富である．ただし，紙と鉛筆や当時のパソコンなどで具体的に計算できるものは限られていた．こうした中，現代数学は飛躍的な発展を見たが，諸科学からもかい離して，産業からも遠のいた．ところが，スーパコンピュータの出現に伴い状況は激変した．複雑で量的にも巨大な対象に対して，ハイテク数学の理論の適用可能性が生まれてきたのである．現代数学の諸科学・産業への応用の新たな夜明けである．物理ベースの伝統的応用分野以外で，最近になり目覚ましい応用が始まったものを例示する．

・　整数論，代数幾何：各種暗号理論（量子コンピュータ実現後も耐え得る）^(3),(4)

・　代数幾何：符号理論^(5),(6)，

・　トポロジー：たん白質の構造解析，物質・材料科学，通信技術（位相的データ解析，パーシステントホモロジー，クイバーの表現論）^(7),(8)

・　代数幾何（特異点論）：学習理論，データ圧縮（確率論）^(5),(9)

・　表現論，微分幾何：コンピュータグラフィックス^(10),(11)

・　微分位相幾何（特異点論）：コンピュータビジョン^(3),(12)

　以上の多くが電子情報通信分野に関わるものである．微分幾何は当然だが，代数幾何なら図形を見る立場から入ると物理，特に素粒子などと相性が良い．代数構造に着目すれば情報系との相性が格別である．ところで4年ごとのフィールズ賞は，過去，確率論関係はほとんどなかった．しかし最近では，確率論関連のテーマが続けて三度入っている．不確定性の扱いが予測・推定の土台となる現代，情報通信サービス分野の諸課題に対しても，その基礎は確率論に負うところが大である．

2.2　幾らでも取れそうなデータ

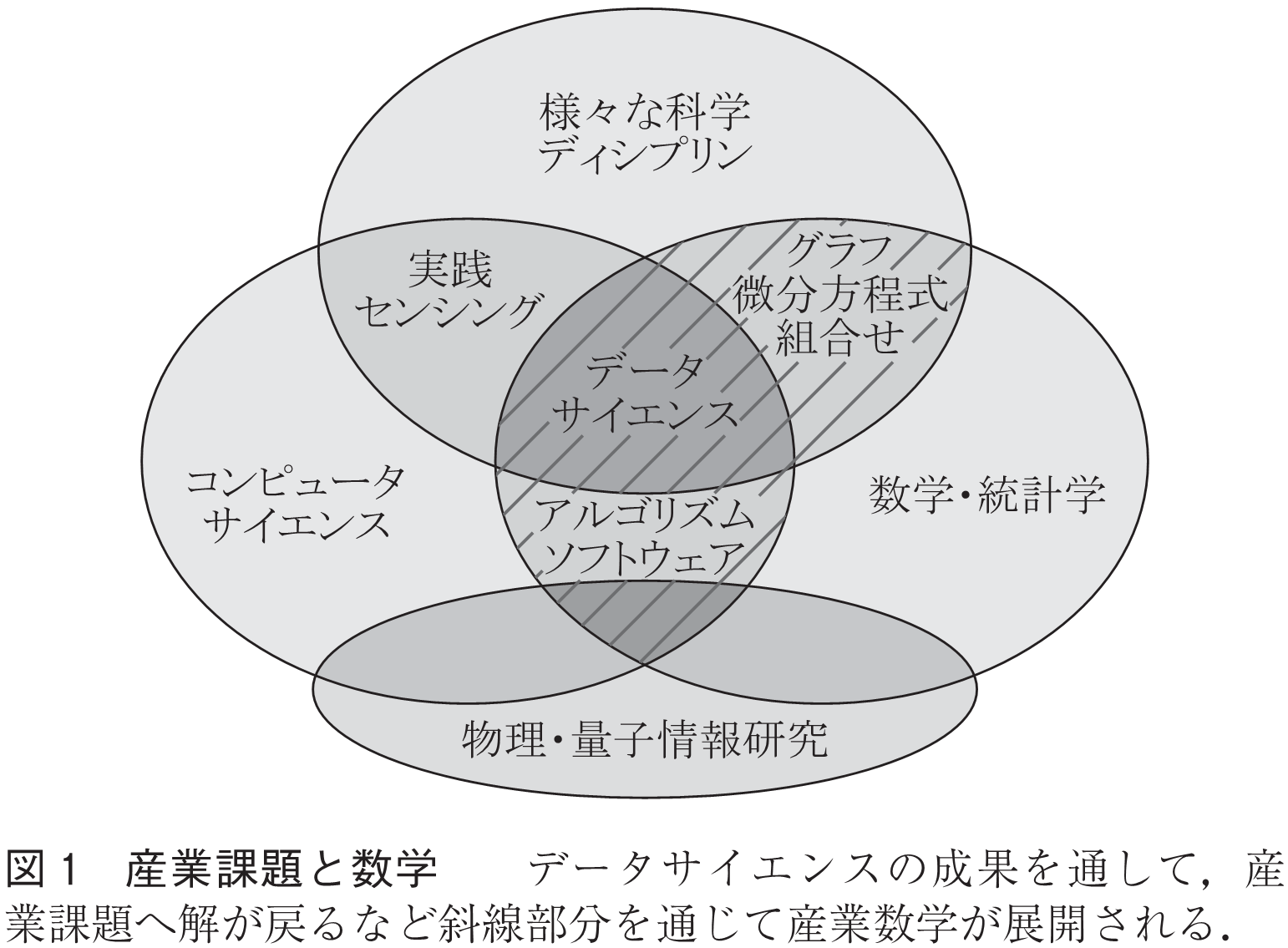
　IMIはInstitute of Mathematics for Industryの略である．だが，マセマティクス・フォア・インダストリ研究所なる日本語表記はいかにも長い．そこでmathをマスとした．こうするとmassとも聞こえる．IMIは，ビッグデータ，IoT，AI（人工知能）を扱う研究所なのである．現在，そして未来の産業分野での数学応用の多くは，これら三つの電子情報通信・インターネット関連キーワードに関わることとなる．ものづくり，医療，農業，環境・エネルギーなど，ほとんど全ての産業に，である（図1）．よく耳にするように，AIの発達もあり，向こう数年で，ビジネスモデルが根底から変わるとの指摘は素直にうなずけるものである．AIという言葉自体が数年のうちに廃れてしまうかもしれない．

2.3　データと数学

　推計統計学の確立者であるとともに，集団遺伝学の創始者の一人であるイギリスの統計学者ロナルド・フィッシャーは次のように述べている．統計学の真価を発揮するのには，どんなデータを集めるかということを考えることが肝心である．統計学はかつて，少ないサンプルデータからいかに有用なデータを取り出し，物事を判断・予測するかということが期待されていた．そのため，センシング技術が発達し，幾らでもデータが収集でき格納できるようになりつつあった頃，つまり情報の時代が到来した当初は，統計学の不要論が10年余り続いたという．しかし事はさにあらず．データマイニングという言葉が示すように，あふれるデータから何をどう読み取るのかが重要になってきたわけである．現在のAIは，確率論を基礎に置く統計学がベースとなる機械学習に軸足を置いている．とりわけ，ニューロンの微視的活動をある種モデル化した深層学習に大きな期待が寄せられている．とは言っても，機械学習は有限個のデータを根拠にした将来予測や未知の状態の探求であるから帰納的である．このことは，未経験の事象に対しては頼りにならず，適応力が低いことを意味している．

　例えばAIによる東大入試突破を目指す東ロボくんプロジェクトでは，数学・物理や知識量が物を言う世界史などは合格点を取れたが，国語や英語は伸び悩み合格点に到達しなかった．特に長文問題は非常に苦手であり，その原因は読解力不足であると指摘されている．国語などに限らず他の科目でも文章題は苦手な傾向があったという．数学を暗記科目だとして指導をしている高等学校があると聞くたびに，残念に思っていたが，入試問題に限れば，過去問を知れば大体解けるという皮肉な結果が如実に現れた．AIの力は，目的に応じた良いデータセットの獲得に基づく．フィッシャーの言葉は今も生きているのである．他方，深層学習が，どうしてこれほどうまくAIとしてワークしているのかの根源的理由は明らかでない．この疑問の解明は，深層学習に加えて，どんな数学を用いればAIがより信頼の置けるものになるのかを探求する際に重要となるだろう．科学研究の伝統的で基本的な方法である，原理と仮定から論理的に結果を導こうとする演えき的推論も，依然，役割を果たさなくなったわけではない．

2.4　数学の使い方

　さて，数学の多くの問題は，やや極論してしまえば

・　逆問題（方程式を立てて解く）

・　最適化問題（条件付き最大最小問題）

の形に集約される．事実，産業や諸科学における種々の数理的問題はこれらの形に定式化される．その上で，手法やアイデアとして，幾何学，代数学，あるいは解析学からのアプローチがある．

　更に，不確定性が付与されるところが現代的課題である．いや，以前から不確定性をいかに取り扱うかは課題であったが，近年，扱われる分野が明示的になってきたのである．実際，いまやはやり言葉となったデータ駆動型研究というのは，データの観察から実際に起こっていることを予測するという意味で典型的な逆問題である．もちろん，データの観測と物理法則あるいはそれを記述する微分方程式等との合わせ技でなされるMRI，CTなどの医療機器開発，高炉の制御も，その典型である．

　このほかにも，数学自体においても関心が高い分類理論というものがある．与えられた特徴を持つ数学的対象の分類を行うのである．何のためにやるかというと，応用上に限っても「与えられた特徴を持つものは，これしかない」と断言できるからである．

　課題解決のための具体的数学的アプローチとして，いわゆる数理モデリングが重要である．モデリングとは，微分方程式やグラフなどを用いて，時間変化する現象の，計測できる主要指標の動きを模倣する“数学の言葉で記述した系”のことを言う．モデルの定式化が鍵であり，定式化の方法により「最適化モデル」「動的モデル」「確率モデル」と呼ばれるもの等がある．また，計算機を駆使するという観点から，本来は連続的に記述する現象であっても，その合理的な離散化，あるいは最初から離散モデルを考えることが多い．

2.5　数値シミュレーション

　厳密には解けない方程式を数値計算により近似的に解くことの重要性と応用上の魅力は明白である．実際，研究開発現場では，有限要素法や粒子法など，数値シミュレーションは欠かせない．これは，数学者にすれば数値実験と言えようが，本当の実験とは違う．事実これらは，あくまで計算機というバーチャルな世界での試行実験でしかない．想定する現象や仮定が曖昧，あるいは方向違いでは正しい答は期待できるはずもなく，計算の過程で数値的な誤差が蓄積して，本来の現象とは全く異なる結果しか得られないことも多い．どんなにたくさんの類似点が確認できたとしても（グラフなどのフィッティング），有限なところを観察しているだけでは，確実とは言い難い．しかも数値シミュレーションでは，コンピュータグラフィックスの力も借りてともっともらしい画像を作ってしまい，間違いに気付き難くなるリスクもある．したがって，数値実験を現象解析のツールとして使用する場合には，注意を要する．例えば実験の場合には，条件設定に自ずから制約がある．ところが，実験に比して数値シミュレーションは，前提としてかなり大胆な条件を設定することが可能なことも多い．それが逆に，幾らでも結果を“今見ている”現象に近付けることを可能にする場合がある．「かくなるはず」との考えにとらわれて前提条件を変更していくと，現実にはあり得ないことを仮定してしまうことにもなりかねない．

　とは言っても，時間と経費が掛かる実験に比べればずっと安上がりに済むと期待される数値実験は，極めて有効な研究手法である．更に，誤差に関しては，現在では精度保証付計算も発展していて，条件が整えば威力を発揮する．

3.1　AI（人工知能）

　昨今のAIブームは三度目であるそうだ．

　筆者が学生であった30年以上も前，コンピュータと言えば，物理的な欠陥やプログラミングの間違いがなければ絶対に正しいとされていた．絶対に正しいことだけを使うのであれば，当時の計算機では，―今のスーパコンピュータでさえも―囲碁において手順のあらゆる可能性を探索すると宇宙時間をはるかに超えてしまう．つまり，間違いを包含するようなコンピュータ（実はアルゴリズム）ができなければ，コンピュータが碁で人に勝てる見込みはない．考えなくてよいはずの不正解をあらかじめ取り除く，つまり，確率論的考え方が必要であるというわけだ．深層学習と強化学習をベースにしたAI，アルファ碁がトッププロ棋士を昨年に引き続き最近もまた破ったのは，その意味でそんなに不思議なことではない．特定機能に特化したAIが，人より確実な仕事をする分野は限りなく広がるだろう．しかし，現在のAIの能力は，巨大な素数判定や素因数分解にも及ばない．RSA暗号が安全な理由だ．したがって，現代のスーパコンピュータの性能を考えれば，AIが人間を超えるとされるシンギュラリティははるか遠い．ただし，ゲームAIの開発者による著書⁽⁶⁾では，知能とはなんだという疑問に技術面から答えようとするため，アニメの身体性や本能も取り上げながら現象学をベースとした考察を展開している．すぐにではないが，計算速度の格段の向上があれば，大量のデータを分析して面白い関係性をAIが見つける時代が来ることも疑いない．なお，関係性を述べる際にキーとなるのは各種インディケータやマーカ等の発見・研究である．これはちょうど，物理などでの保存則の記述に必要な不変量の研究と似ている．

　機械の発明により，多くの肉体労働が機械にとって代わられた．同様に，AIの発達により多くの職業が機械に置き換えられていく．‘ひと’は視覚の動物と言われている．今回，AIという機械は，視覚優先の仕事が核となるビジネスにおいて人の仕事を奪うのかもしれない．

3.2　現実の量子コンピュータ

　現在の計算機の性能は，半導体素子の加工プロセスの微細化に負ってきた．集積密度の向上である．しかし微細化にも限度があり，チップを作るために描く線は原子より細くはできない．そのため，いわゆるムーアの法則は終えんする．ところが，現代の産業の要請から現れる重要で困難な問題は，不確実性を伴った最適化問題として定式化されることが多い．そのため，超高速化を狙い量子力学的現象を計算に利用する計算機需要は計り知れず，数学ベースの量子的アルゴリズムの可能性は大きい．

　産業数学は産業が要請する問題を物理，化学，生物，人文・社会科学などのサイエンスと共同して解決する数学である．ただし，昨今の産業課題では，ビッグデータ，IoTなどにより純粋に数学だけの問題として定式化されるものが増加している．例えば，組合せ最適化問題に帰着されるものは大概そうである．

　組合せ最適化問題と言えば，従来型のコンピュータを使うシミュレーテッドアニーリングやD-Waveで知られる量子アニーリング計算機・イジングマシーンが有名である⁽¹⁴⁾．共に，磁性体（スピンモデル）の統計力学的モデルであるイジング模型を基礎に置いている．組合せ最適化問題，つまり条件付きで最小値を求める問題を，イジング模型の最低エネルギー状態を求める問題に置き換えて解くのである．前者では極小値でとどまり別の処方箋を使わねばならないところを，後者は量子トンネル効果の利用により，見事に最小値まで到達できる．ただし，このような最適化問題に威力を発揮するが，例えば素因数分解などは得意ではない．また，厳密解の獲得が困難なことも多くあり，なぜ，そううまく計算できるのか不明な点も残っているという．他方，量子コンピュータ（ゲート式）は，常に正解を出す従来型コンピュータとは異なり，何回かに一度正しい答えを導き出す．したがって，素因数分解など結果の正誤が容易に判定できる問題に向いている．いずれにせよ，量子ウォーク⁽¹⁵⁾，量子シミュレーションなど，デバイス設計以外での量子力学的現象の数学的研究は今後の産業数学の大テーマの一つである（表1）．例えば，イジング模型を超え，高次元の磁性模型を利用した最適化問題へのアプローチなども考えてみると興味深いかもしれない．

　今のスーパコンピュータの計算速度を超える量子コンピュータ実現には，更なる技術開発が必要とされている．2012年のノーベル物理学賞は，「単一量子系の測定や操作を可能にするための革新的な実験的手法」によりHarocheとWinelandが受賞した．具体的には，非局在量子もつれという性質がもたらす遠隔作用が存在し，二つの粒子が何の媒介もなしに同期して振る舞うことを利用する革新的技術の開発である．このような直感に反する効果への数学・量子情報研究の進展が待たれる．