1．情報ネットワークの役割とそれを支える新たな基礎理論の必要性

　現代社会は100年前では全く想像し得なかった各種の技術革新に支えられており，高い利便性や効率性を持つ社会システムが実現している．中でも情報ネットワークの普及による社会の変化は最も目覚ましい技術革新の一つであり，既に情報ネットワークのない社会は考えられないほどに日常生活に浸透し，快適な日常生活や高効率な社会活動を支える社会インフラとなっている．通勤・通学中の電車内にて多くの乗客がスマートフォンでYouTubeの視聴やオンラインゲームに興じる姿は，距離段階・時間帯ごとの時間課金であった固定電話の時代から見ると隔世の感がある．それどころか，今や人間の生命や財産に関わる事柄まで情報ネットワークに強く依存していて，それが停止したときの社会的影響が日増しに大きくなっている．例えば東日本大震災後の緊急支援物資の物流システムにおいて，情報ネットワークの障害が原因で避難所の需要に合った物資の配送を困難にしたことは記憶に新しい．このように，情報ネットワークは常に安定運用することが期待されるクリティカルインフラとなっているのである．

　情報ネットワークの日常生活への浸透は，個人間のコミュニケーションや個人レベルの情報発信を飛躍的に活性化し，社会活動の利便性や効率性を向上させている．その一方で，実世界とサイバー空間の密接な結び付きにより，人間の群集心理をあおって実世界に影響を与えたり，ネットアクセスの過度な集中により情報ネットワークの安定運用に支障を来すなどの問題が実際に起こっている．特に，情報ネットワークによる情報流通の迅速性や匿名性は，世界各国で起きている組織的なテロ行為などの犯罪に利用されているだけでなく，これまで情報統制による開発独裁を敷いてきた国家に対して，その統治体制さえも揺るがしかねない力を持ち始めている．また，人間以外にも例えば金融市場のアルゴリズム取引など，ネットワークに接続されたコンピュータが情報ネットワークを介して実社会の経済に大きな影響を与えるようになってきている．あらゆるものが情報ネットワークに接続されるIoT時代の本格的な到来を控え，情報ネットワークの安定運用は，もはや情報ネットワークそれ自身だけでなく，それにつながる人や‘もの’まで含めて「拡大されたネットワークモデル」を対象にして相互の影響を考察しなければならない状況である．

　このように，良くも悪くも社会と不可分に結び付いた情報ネットワークでは，社会的な悪影響を緩和しつつ安定的に運用することが重要である．社会の状況と結び付くことで「拡大されたネットワークモデル」の構造は複雑化し，悪影響が拡大する速度も爆発的に速くなることで，適切な対処が難しくなると予想される．しかし，元々のこれらの状況は情報ネットワークの影響力によって生じているので，我々が直接オペレーションできる対象が情報ネットワークに限定されていたとしても，何らかの有効な対策を講じることができるはずである．少なくとも，緊急時に最悪の事態に陥らないよう，個別の事情に特化した本質的な対処がなされるまでの間，情報ネットワーク側で何らかの激変緩和措置を実行することができるかもしれない．そのために必要なことは，情報ネットワークとそれにつながる人々の振舞いを同時に考慮し，情報ネットワークや人々との相互作用とその影響を理解することができる基礎理論の確立である．これまでも情報ネットワーク分野では待ち行列理論や最適化理論など，様々な基礎理論に基づいて技術開発が行われてきた．それらの基礎理論の重要性は今後も変わらないが，新たに重要性を増した「拡大されたネットワークモデル」において，社会を巻き込んで爆発的に拡大する事象の発生要因を理解し，その対策技術の検討を可能にする新しい基礎理論が必要とされているのである．

　かつて電話網の回線設計において，特定の条件下で電話の発呼はランダムであるとされ，このモデル化は大いなる成功を収めた．本来，それぞれの発呼の背後には人々の営みや個別の事情があるはずだが，個別の事情によらないモデル化を行うことで普遍性のある取扱いに成功したと言える．情報ネットワークとユーザの相互作用で起こる現象として「ネット炎上」を考えてみよう．具体的には様々なパターンのネット炎上があるかもしれないが，一言で言えば情報ネットワークを介してユーザの振舞いの活性度が発散するような現象である．ネット炎上にもそれぞれに個別の事情があり，社会科学的または行動心理学的にそれぞれの事情を説明する個別のモデルが作れるかもしれない．しかし，電話の発呼のモデル化に倣うと，それぞれの個別の事情はあえて無視し，個別の事情に左右されない工学的に共通する現象を抜き出すことが，普遍性のあるモデル化につながるのではないだろうか．また，緊急時にその個別の事情を分析することなく，速やかに激変緩和措置を講じるためにも，個別事情によらない普遍性のあるモデル化が重要である．

　近年，通信ソサイエティでは情報ネットワーク分野の新たな基礎理論を整備する必要性が認識され，時限研専として情報ネットワーク科学研専や通信行動工学研専などが設立され活発な活動が行われている．今回，創立100周年記念懸賞論文の機会をお借りして，筆者が関連する（未来へつなぐための）新しい基礎理論整備への取組みを概説したい．可能な限り数式を用いないよう工夫しながらイメージを伝えることで，多くの方に新しいネットワーク基礎理論の胎動をお伝えできれば幸いである．

2．ネットワーク上の振動モデルとノード中心性の拡張

　個のノードから成るネットワーク構造をの正方行列で表現して，その固有値・固有ベクトルなどからネットワーク構造やダイナミクスを調べる方法は，スペクトルグラフ理論として知られている⁽¹⁾．一般に，正方行列が対称（行と列の入替えで不変）ならば多くの都合の良い性質が成り立つため，スペクトルグラフ理論は対称行列で表現可能な無向グラフに関して多くの有用な結果が知られている．一方で，非対称行列で表現される有向グラフへの適用は難しく，GoogleのPageRank⁽²⁾はその数少ない成功例の一つである．

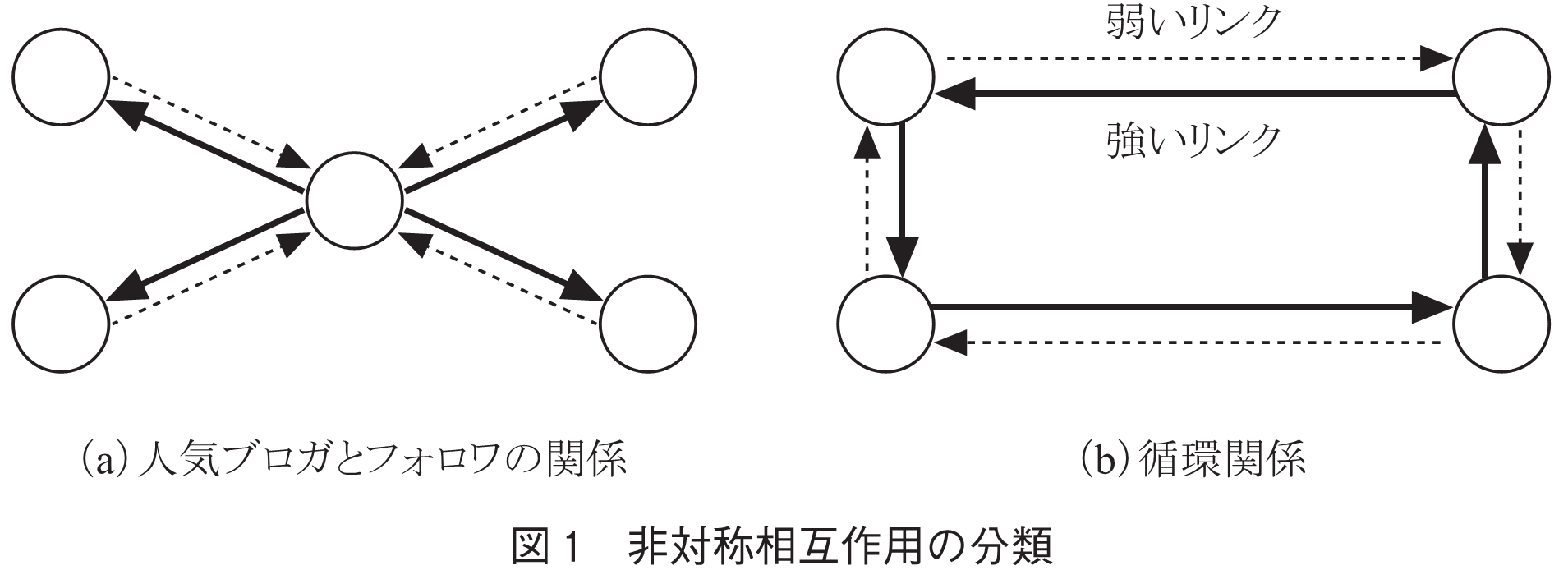
　人を対象としたネットワークでは，人と人の関係の強さは非対称であり，人をノード，人と人の関係をリンクとすることで非対称行列で表現される有向グラフとなる．しかし，有向グラフであっても対称行列で表現可能な性質の良いクラスが存在する．図1は非対称性の分類の典型例を示したもので，図(a)は例えば有名ブロガとそのフォロワの関係などに見られる構造であり，図(b)はじゃんけんのような関係である．どちらも有向グラフであるが，(a)はリンクの非対称性をノードの特性（中央のノードが強く，周囲が弱い）に還元することで，リンクの対称化が可能である⁽³⁾．一方，(b)の関係はノードの特性に還元できない純粋なリンクの性質である．有向グラフに関するスペクトルグラフ理論の成功例は，(a)のような「対称化可能なクラス」を対象としたものである．

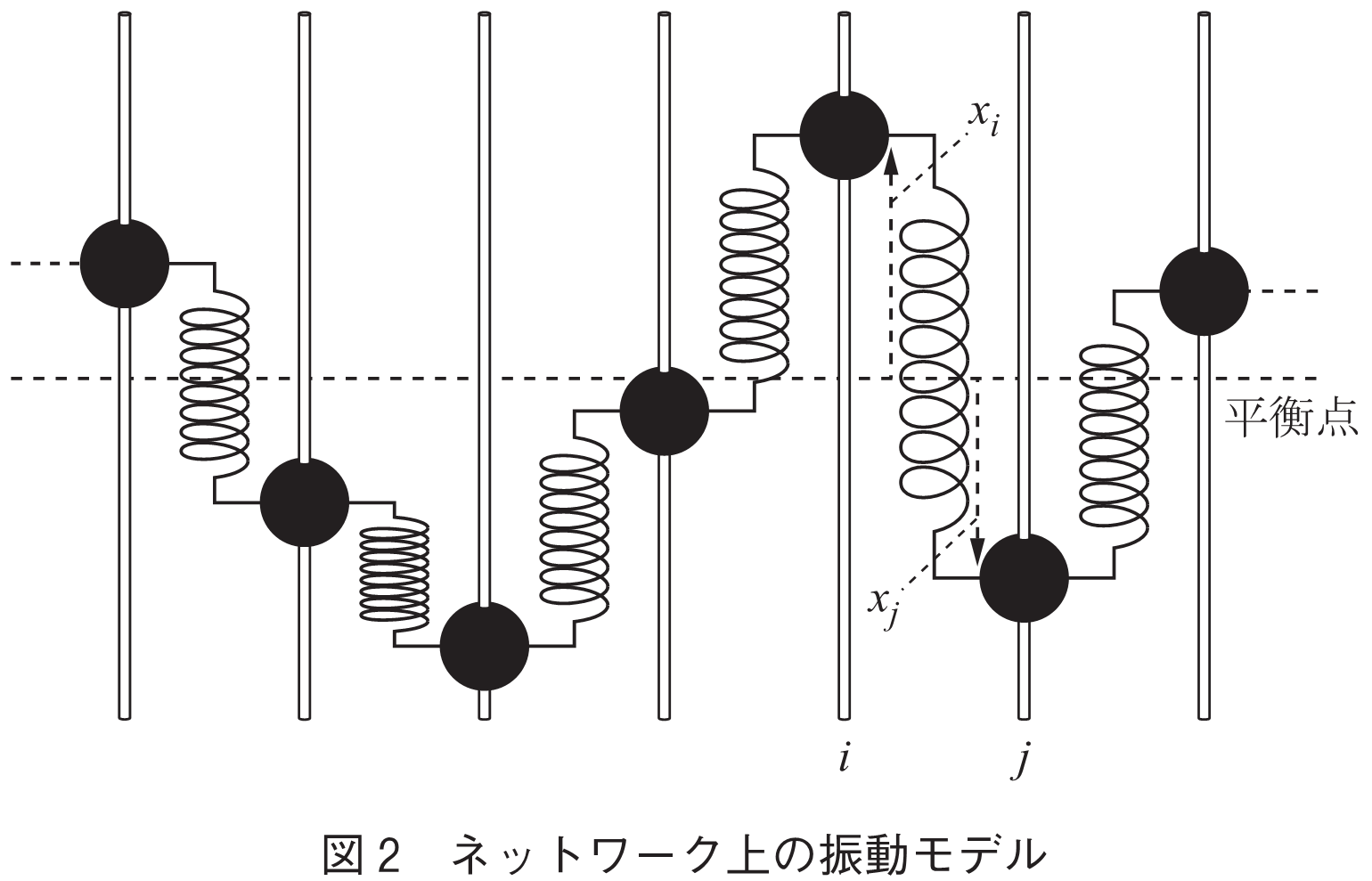
　対称化可能な有向グラフに関連していて，かつネットワーク上で人と人の影響の伝搬を表現するモデルとして，ネットワーク上の振動モデルを考えよう⁽³⁾．各ノードが時刻で変位という状態量を持ち，隣接ノードと自分の状態量の差に比例して，隣接ノードの状態に合わせようとする復元力が働くモデルである．図2は一次元ネットワークの場合を図示したものであるが，一般のネットワークトポロジーでも同様である．まず，このモデルが極めて自然でかつ基本的であることを説明したい．全てのノードの状態量が等しい場合，ノード間の影響がない安定状態であると考えるのは自然である．次に，ノードの状態量が隣接ノード間で異なる場合，その「差」が大きいほど安定状態に向かう大きな復元力が働くと考えるのも自然である．もし状態量の「比」によって復元力が働く場合も，適当に対数を採れば「差」として考え直すことができる．復元力の強さが「差」に関するどのような関数型であっても，安定状態の回りでテイラー展開すれば，第一次の近似として「状態量の差に比例」した復元力が現れる．したがって，図2のようなばねのモデルは，多くのモデルが共通して含んでいる特性を記述する基本的なモデルなのである．

　この振動モデルを分析すると，運動方程式に「対称化可能なクラス」の有向グラフに対応する非対称行列が現れる．これは，ノード間の影響が非対称であっても，その非対称性はノードの特性に還元できることを意味しており，この場合のノードの特性はノードの質量に対応する．また，対応する有向グラフが「対称化可能なクラス」であることは，ノード間に働く力がニュートンの第三法則（作用・反作用の法則）を満たすことと等価である．これらの理由で有向グラフを対称化することができ，対称行列を対角化する（実対称行列は常に対角化可能）ことで運動方程式を解くと，個の独立な調和振動子（普通の振り子）の運動方程式に分解することができる．この数はノード数と等しいが，決して各ノードが独立な振り子になっているわけではないことに注意してほしい．各ノードは図2のように密接に関連しているが，ネットワーク全体として種類の振動モードが現れ，それぞれが独立な振り子と等価な振舞いをする，という意味である．

　このように「対称化可能クラス」に属する振動モデルは図2のような普通の力学モデルに対応し，各ノードの振動解は独立な振り子による振動の重ね合わせで表現され，その振舞いは完全に理解することができる．しかし，振動解は一般に複素関数であり，実部のみを取り出したとしても負の値をとる場合もあり，ノードの変位がどのように具体的な概念と結び付くか考える必要がある．

　具体的な話に入る前に，ノード中心性の概念に触れておく．ノード中心性とは，ネットワークの中で特定のノードがどのくらい重要な働きをしているかを定量的に表したもので，重要性の基準の採り方によって様々なノード中心性の概念が存在する．次数中心性とは，ノード次数（ノードにつながっているリンクの本数）を中心性の指標としたもので，ノード次数の高いノードほど情報の伝搬に強く寄与することを評価した指標である．媒介中心性とは，任意の2ノード間の最短経路が自ノードを通過する割合を中心性の指標としたもので，多くの最短経路を中継しているノードが高く評価される指標である．また，GoogleのPageRankもノード中心性の一つであり，振動モデルにおけるノードの質量と関連している．

　振動の強さを非負の値によって表現するために，ノードの振動エネルギーを考えてみよう．すると，ノードごとの振動エネルギーがノード中心性の概念に結び付くのである⁽⁴⁾．全てのリンクの重みをとしてノードごとの振動エネルギーを考えると，次数中心性に比例した値を与え，リンクの重みを任意の2ノード間の最短経路の通過本数で与えてみると，ノードごとの振動エネルギーが媒介中心性に関連する値を与える．このことは，異なるノード中心性の概念を共通の枠組みで理解したことになる．また，ノードの変位はそれ自体で物理的な意味があるわけではなく，ノードの運動エネルギーを考えることでネットワーク内でのノードの働きの強さを表現することになる．ただし，ノードの変位を介してノード中心性を理解することは決して無意味ではない．ノードのアクティビティがネットワーク内を伝搬するには，その背後にノードの変位に基づく波の構造が必要なのである．

　更に重要なのは，ノードの振動エネルギーがノード中心性の拡張概念に結び付くことである．リンクの重みやノードの重みを変えることで，様々な中心性の尺度を作り出せるのはもちろん，運動方程式の初期条件を変えることで，特定のノードがアクティビティの起点となった場合のノード中心性なども自然に得られる．また，一般に振動現象とは運動エネルギーとポテンシャルエネルギーが入れ替わりながら変化することから，ノードの運動エネルギーのみを考えることにより，ネットワーク上のノードのアクティビティの伝搬の経時変化を記述することもできる．

3．ネット炎上のモデル化と対策技術

　前章では，「対称化可能な有向グラフ」で記述可能なネットワーク上の振動モデルは，図2のような普通の力学モデルで表現でき，本質的に個の独立な振り子の運動に分解されることを述べた．このことは，幾ら時間が経過してもネット炎上のようなノードのアクティビティの強さ（ノードの振動エネルギー）が発散するような振舞いは出現しないことを示している．ここでは，ネットワーク上の振動モデルを「対称化可能な有向グラフ」を超えて一般の有向グラフに拡張することを考える．

　一般の有向グラフに対応する振動モデルでは，ノード間の復元力に対してニュートンの第三法則が成り立たない．つまり，図2のような普通の力学モデルで表現できるような現実世界の振動現象には対応せず，ネットワーク内での仮想的な振動モデルを扱うことになる．少しだけ数式を使って表現すると，ノードの変位を並べた列ベクトルに対して，時間発展を表す運動方程式（波動方程式）は

と書ける．ここで，を有向グラフ上の二階差分の操作を表す行列（ラプラシアン行列）としたとき，とはのようにラプラシアン行列を分解したもので，が対称化可能な有向グラフのラプラシアン行列，はそれ以外の，ノード間に高々一方向しかリンクのない有向グラフのラプラシアン行列である．は「対称化可能な有向グラフ」であるが，が存在することによって独立な調和振動子への分解が阻害され，複雑な振舞いをすることになる．

　前章では（はゼロ行列）となる状況を考えており，は対称化可能なので固有値が実数であることが保証されていた．しかし，となる状況を考えるとの固有値は一般に複素数となってしまう．ネットワーク上の振動現象が時間とともに減衰する効果も取り入れると，一般の有向グラフ上での振動モードの解の構造は

となる．ここでである．の固有値が実数ならば2番目の指数関数は純粋な振動を表すが，固有値が複素数になると2番目の指数関数の中身が純虚数にはならず，実部が出現する．この影響が減衰の強さを超えれば，解が時間とともに指数関数的に発散する．このことは，ネット炎上のような爆発的なダイナミクスが「拡大されたネットワークモデル」から発生するメカニズムを表現するものであると解釈することができる⁽⁵⁾．

　発散が生じる仕組みが分かると，それを起こさない条件を考えることでネット炎上の防止技術を検討することができる．有向グラフが「対称化可能な有向グラフ」であることは，発散が起こらないための十分条件である．そのためにはの影響を排除するような操作ができればよい．実はの分解は一意的ではないので，操作のしやすい都合の良い分解を選ぶことができる．具体的には，ネットワーク上に閉路を考え，全ての閉路でリンクの重みの積が右回りと左回りで等しければ「対称化可能な有向グラフ」である．そのためのリンクの重みの調整は，閉路上のどのリンクに対して実施してもよい．この任意性がラプラシアン行列の分解の自由度と関連している．

4．有向グラフ上のスペクトルグラフ理論と量子論

　一般の有向グラフ上での振動現象を十分理解するためには，の影響によってネットワーク上の振動現象がどのように影響を受けるのかについて，因果関係を明示的に理解することが可能なモデル化が望まれる．まず先ほどの波動方程式(１)について「対称化可能な有向グラフ」のラプラシアン行列を対角化するように変換した波動方程式を考えると

のようになる．ただし，はを対角化した行列で，対角成分はの固有値であり，それ以外の記号はの対角化に合わせて変換したものである．このとき，の影響（つまりの影響）を明示的に理解するためには，変換した波動方程式(２)の解であるが，の影響との影響を表すそれぞれの関数の積となるように，両者の影響が分離して与えられることが望ましい．しかし，実際に試してみると，このような積形式解の試みは成功しない．その理由は，波動方程式(２)が時間に関する二階微分の方程式であるがゆえに，積形式の関数を代入すると余計な交差項が生じるためである．

　この問題を回避するために，

を満たす線形作用素の存在を仮定し，時間に関して一階微分である以下の時間発展方程式を考える⁽⁵⁾．

時間発展方程式(４)の解は

から，元の方程式(２)の解にもなっている．更に（当初の想定より数式が多くなってしまうが）積形式解の可能性についても考えよう．まず，としての分解

を考える．また，解の積形式解として以下の関数形を仮定する．

ただし，式(５)，(６)に現れる関数は，以下の方程式

を満たすベクトル，，及びはベクトルの成分を対角成分に持つ対角行列である．ここで，式(８)をとしなかったのは，以下の計算をするとすぐに理解できる．

　式(４)に式(６)を代入すると，

となり，積形式解(６)の試みが成功することが分かる．このように，時間発展方程式(４)は有向グラフ上の振動現象を理解するための基礎方程式であるとみなせる⁽⁵⁾．

　ここで，基礎方程式(４)と量子論の関係について触れておきたい．基礎方程式(４)は，物理定数などを無視すれば，形式的には量子論に現れるシュレディンガー方程式と同じである（正確には相対論的量子力学に現れるディラック方程式に対応する）．量子論とは，原子，電子，光子などのミクロな世界を記述する物理理論であるが，方程式(４)はミクロな世界とは関係なく，対称化できない有向グラフの影響を考慮した複雑な振動現象の絡み合いを，因果関係を明示して理解するために到達したものである．このことから，量子論的な方程式は決してミクロな世界を記述するための特別な枠組みなのではなく，振動現象の因果関係を理解するための一つの「ものの見方」であるという解釈が可能である．

　ただし，量子論とは異なり一般の有向グラフではがエルミート作用素にならない．このことが，ネット炎上のようなエネルギー保存則を破る現象の出現要因となる．

　さて，基礎方程式(４)を実際に応用するためには，式(３)を満たすの具体的な構成方法を明らかにしなければならない．式(３)を満たすは一意には決まらないが，式(３)さえ満たしていれば元の波動方程式(２)を満たすので，都合の良い選び方を採用すればよい．とのグラフ的な関係が明示できるような対応関係を探す取組みは，行列の成分を普通の数であるとした通常のやり方に加え，二乗するとになるべきゼロ性を持つ代数の利用や，二次元の特殊ユニタリ群SU(2）の生成子を用いて積の順序を交換すると符号が変わるような代数を利用した簡略化なども検討している．

　以上のように，情報ネットワークを介した人と人の相互作用から生まれるダイナミクスを理解するために，ネットワーク上の仮想的な振動現象に基づく新しいネットワーク基礎理論が生まれつつある．そこでは，ネット炎上などの爆発的なダイナミクスの工学的モデルを与えるともに，因果関係の明示という観点から量子論という従来の情報ネットワーク工学分野にはなかった概念が自然に導入される．ネットワーク上の振動現象が，一方で伝統的なノード中心性との関係で従来のグラフ理論の結果を包含しながら，他方で量子論的な枠組みに結び付くという壮大な可能性を感じて頂けたのではないだろうか．このような未来につながる基礎理論の展開が，来るべき超ネットワーク化社会のための新しい情報ネットワーク技術を支えていくものと期待している．

文　　　　　献