Vol.100 No.6 (2017/6)　目次へ

タイトル

松下春奈　正員　香川大学工学部電子・情報工学科

Haruna MATSUSHITA, Member (Faculty of Engineering, Kagawa University, Takamatsu-shi, 761-0396 Japan).

電子情報通信学会誌　Vol.100 No.6 pp.489-492 2017年6月

©電子情報通信学会2017

1．は　じ　め　に

　筆者は学生時代からこれまでにおいて，NOLTAソサイエティの核である非線形問題（NLP）研究専門委員会（以下，研究専門委員会は研専と略す）を主研究会として活動してきた．NLP研専は，非線形系や複雑系の理論や解析，制御やその応用，また，世の中に実在する非線形現象やそれらによる諸問題に関するありとあらゆる研究を扱う研究会である．今日の筆者があるのは，このユニークなNLP研専を通じて御指導御鞭撻を下さった諸先生方のお陰である．

　そんなNLP研専において，筆者は長年，教師なしニューラルネットワークによるクラスタリング技術や，群知能メタヒューリスティックアルゴリズムによる非線形最適化に関する研究を発表してきた．また近年では，群知能型最適化手法の，スイッチ力学系^(用語)の回路設計パラメータ探索⁽¹⁾やE級増幅器の回路設計⁽²⁾への応用を提案している．そのような中，筆者が現在取り組んでいるのが，群知能型非線形最適化手法による手軽かつ高精度な非線形解析手法の提案に関する研究である．これは，筆者のソフトコンピューティング技術に関する経験を，長年のNLP研専での活動を通じて得た非線形問題に関する知識と融合させた独創的なアイデアに基づくものである．

　本稿では，まず非線形解析の重要性を述べた後，筆者が提案する新しい非線形解析手法を紹介する．更に，非線形解析とその関連分野の技術が今後どのように発展し，また活用されるかについて，個人的な意見を楽観的に述べさせて頂く．

2．分岐解析をはじめとする非線形解析

2.1　非線形解析の重要性

　現代の私たちの社会における解決すべき重要課題は，工学，医療，自然科学等の多種多様な分野に及んでいる．特に，脳，感染症，エネルギー，通信，経済，天気などは，一定の規則に従って時間の経過とともに状態が変化することから力学系として捉えることができ，様々な数理モデルが提案されている．力学系の有効な解析手法に，分岐解析やカオス解析をはじめとする非線形解析がある．諸問題の数理モデルを非線形解析する場合，最も基本となるのが平衡点を含む周期点の解析である．また分岐解析は，システムのパラメータを変化させたときのシステムの性質の急激な変化，つまり，周期点の安定性などの変化を調べることを言う．例えば，生体モデルの分岐解析は，神経細胞ネットワークの状態遷移機構の解明という医療問題への応用の足掛かりとなり，自動車の運動特性の分岐解析は，効率良く安全なタイヤ特性を理論的に見つけることを可能とする．このように，非線形解析を行うことでシステムを詳細に分析することができ，これにより諸問題の解決，最適化，制御，予測につなげることができるのである．

　多岐にわたる分野においてこれほどまでに重要な非線形解析であるが，いまだ統計的解析しか行われない分野も多く存在する．その理由の一つが，非線形解析の難解さにあると考えられる．例えば，システムの全体像の理解に必要不可欠な周期点は，多くの場合手計算での導出は困難なため，何らかの数値計算を用いることとなる．そこで，非線形解析の分野で広く利用されているのがニュートン法である．ニュートン法を用いるということは，勾配情報を利用するために微分を行うということであり，また，ニュートン法は初期値の設定を適切に行わないと正しい解が求まらない．これらが，数理モデル化されていない多くのシステムにとって非線形解析に取り組むための大きな壁となっていると考えられる．更に，周期点解析の応用である分岐解析は，周期点条件と分岐条件の二つの条件を満たす解を導く必要があることから，様々な数学的・力学系的知識や経験，ノウハウを必要とする高度な解析手法であると言える．

　一方，ニュートン法に変わるメタヒューリスティックな数値計算の手法として，粒子群最適化法（PSO: Particle Swarm Optimizer）⁽³⁾が広く知られている．PSOは最もシンプルな群知能型最適化アルゴリズムの一つで，粒子と呼ばれる複数の解候補が，互いに情報を共有しながら探索空間を移動することで最適解へ収束するという性質を持っている．アルゴリズムが簡素であること，勾配情報を用いないこと，改悪方向への更新を許すこと，局所解を含む最適化問題にも有効であること等から，幅広い分野で利用されている．

2.2　入れ子構造形PSOによる分岐点探索手法

　筆者はこれまでの群知能型最適化手法に関する知識を非線形解析へ応用することで，PSOによるスイッチ力学系の分岐点探索手法を提案した⁽¹⁾．これは，目的関数を周期倍分岐条件とすることで，PSOにより分岐点を導出する手法である．ニュートン法とは大きく異なり，微分による勾配情報を必要としないことから，広大な多次元パラメータ空間から短時間で高精度な分岐点を導出することを可能とした．一方で，分岐点導出の際に必要となるもう一つの条件，周期点条件については手計算で厳密に求める必要があり，汎用性が高いとは言えなかった．

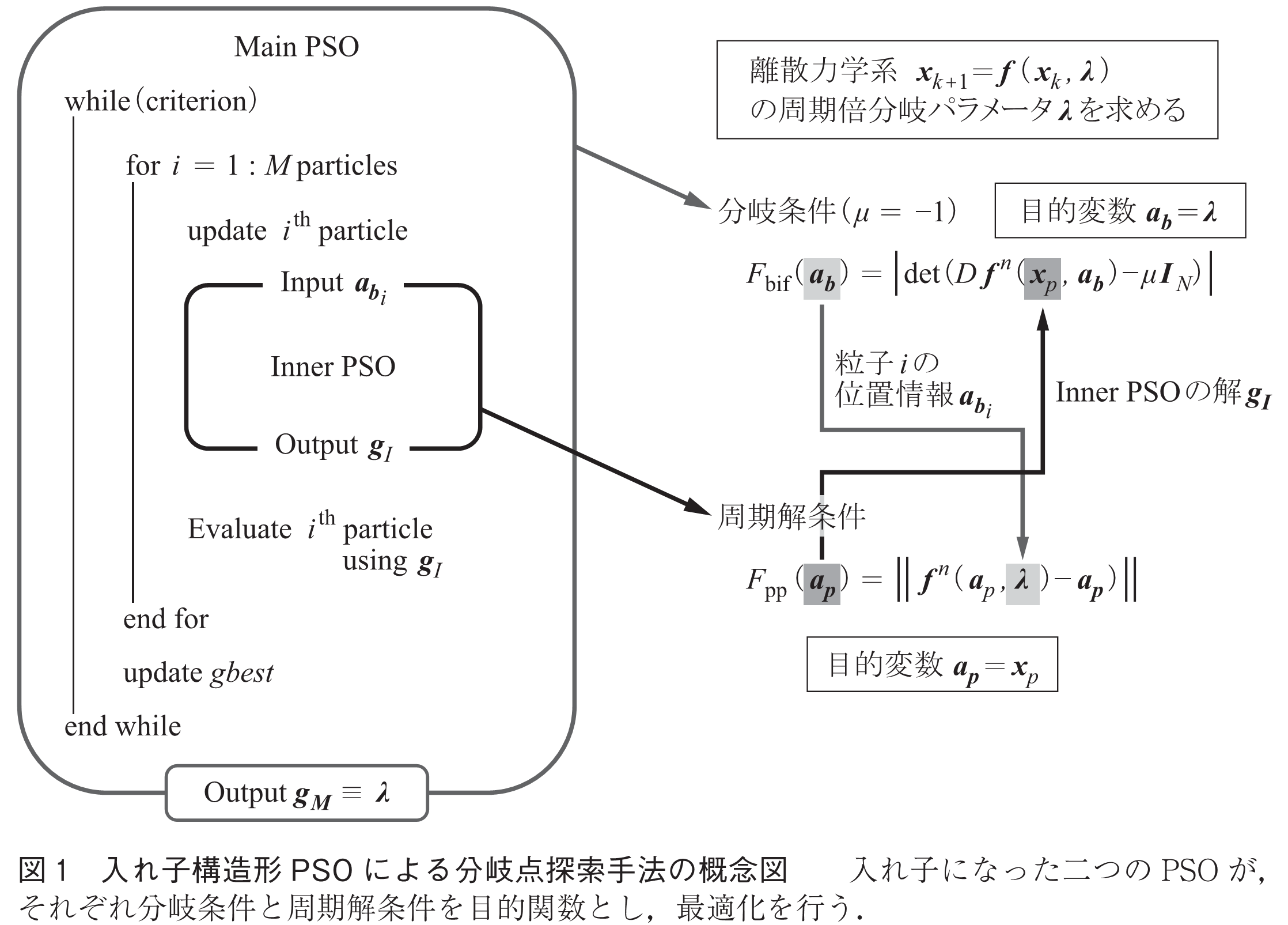
　そこで筆者らは，入れ子構造形PSOによる分岐点探索手法⁽⁴⁾を考案することで，より手軽かつ高精度な分岐解析手法の実現を目指している．この手法は，入れ子構造を持つ二つのPSOで構成されている（図1）．一つは周期点を探索するPSOで，それが分岐点を探索するもう一つのPSOに内包されている．これにより，状態空間とパラメータ空間を混ぜることなく，両方の制約条件及び最適化条件を満たしたパラメータを探索することを可能とした．

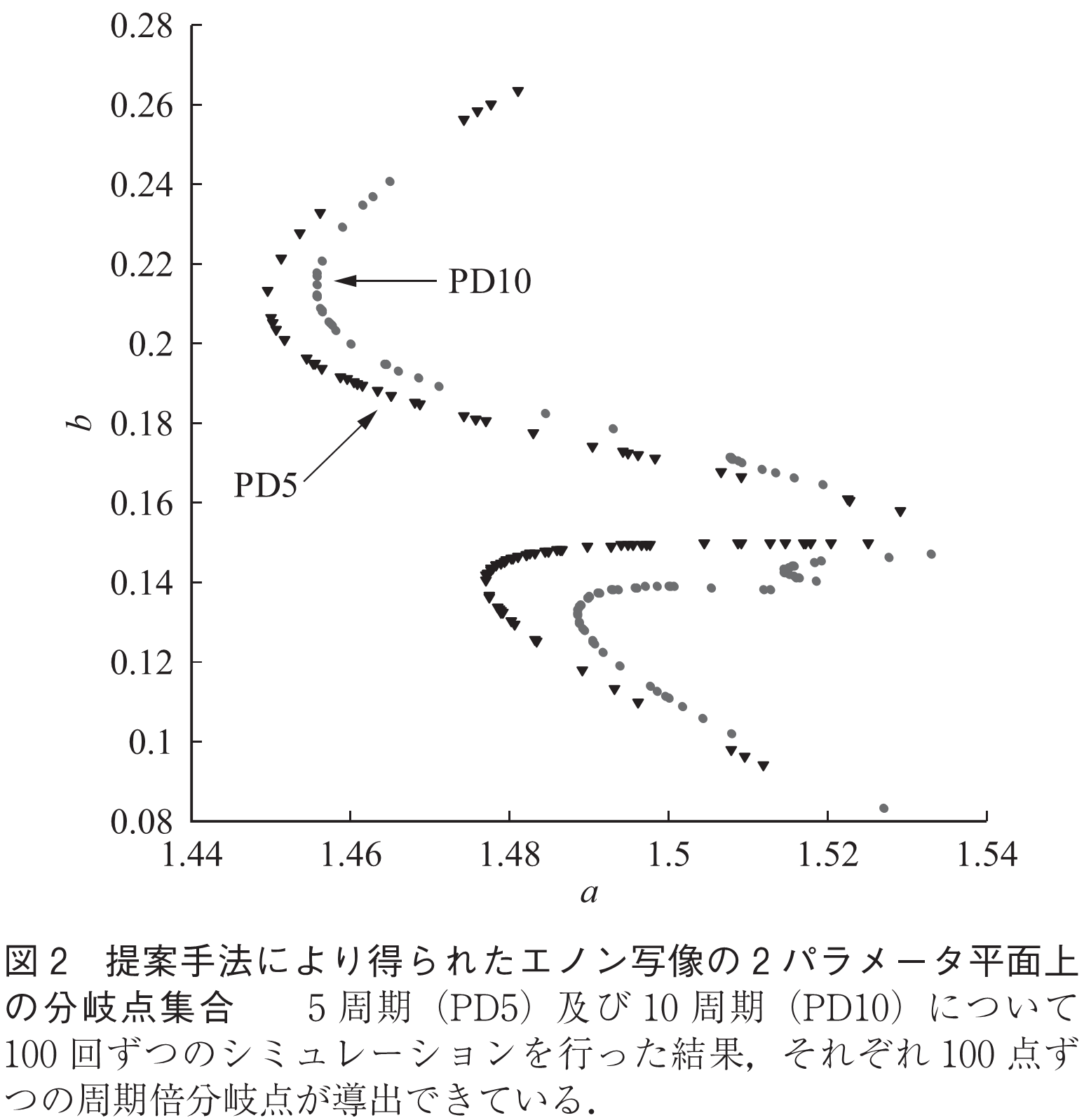
　離散力学系としてよく知られているエノン写像に提案手法を100回ずつ適用し，得られた100個ずつの分岐点を2パラメータ平面上に描写した結果が図2である．これは，1パラメータずつ細かい区間に刻んで探索したものを組み合わせたのではなく，2パラメータ空間から一気に二次元分岐パラメータを直接的に探索した結果であることに注意されたい．5周期（PD5）と10周期（PD10）の周期倍分岐点集合を導出できていることが見て取れる．これらの分岐点は周期点の安定性に依存することなく，高精度かつ短時間での導出が可能である．また，理論的には50周期であろうが100周期であろうが複雑な式変形なしに対応可能で，複雑な初期値設定やパラメータ設定をする必要もない．現在は離散力学系の周期倍分岐への適用例しか発表していないが，連続力学系への適用，及びサドルノード分岐やNeimark-Sacker分岐，更に，Grazing分岐やBorder-Collision分岐のようなスイッチング動作を有する合成力学系特有の分岐への応用を順次行っていきたいと考えている．

2.3　提案手法の利点と期待される波及効果

　提案手法は煩雑な式変形や注意深い初期値設定，厄介なパラメータ設定を必要としないため，従来はノウハウなしには行えなかった分岐解析の簡略化へ貢献するだけでなく，微分不可能なモデルの分岐解析を可能とするのではないかと考える．つまり，多くの現象やパラメータを含んだ高次元数理モデルの開発，及びそれらの詳細な非線形解析が期待できる．これにより，生体や自然現象等様々な分野の精密な理解，制御，予測，発展が期待できる．

　分岐解析は，非線形的挙動を取るあらゆる系にとって重要である．これは，数理モデルのみならず，自動車や電気回路，自然現象など実社会の多岐にわたる．一方，通常用いる数理モデリングでは，実社会現象では必ず存在する不確かなダイナミクスの存在を無視することができない．しかしながら，本手法はメタヒューリスティック手法を用いていることから，不確かさを含むシステムや雑音を含んだシステム，動的に変化するシステムにも柔軟に対応可能ではないかと考える．これにより，従来の工学システムを非線形解析の観点から再検討することで，従来法では実現が困難あるいは不可能であった高性能でロバストな装置・システムを，効率的に作り出すあるいは制御することが可能になるのではないかと期待している．

3．非線形解析と未来予想

　本章では，非線形解析とその関連分野の技術が今後どのように発展し，また活用されるかについて，個人的な意見を楽観的に述べさせて頂く．

　分岐解析やカオス解析をはじめとする非線形解析理論に関する研究は，世界中の研究者によって長年行われてきた．一方，近年の計算機性能の急速な発展により，これまではスーパコンピュータをもってしてしかできなかった高次元かつ複雑な数理モデルのシミュレーションが，個人でも手軽にできるようになってきた．これら非線形解析に関する緻密な理論と，コンピュータによる力強い計算力とを組み合わせることで，未知なる現象の発見や様々な非線形現象の高精度な予測が，どんどん花開いていくのではないだろうか．

　2．で紹介させて頂いた筆者らの提案手法も，計算機技術の発展なしでは成し得ない手法である．勾配を用いる最適化手法は微分系への式変形や注意深い初期値設定を必要とする反面，計算量は少なく，またその性能は理論に裏付けられている．一方，PSOをはじめとする群知能法は集団で同時に解探索を行うので，勾配法と比較して計算量は多くなる上，必ずしも最適解を見つけられる保証もない．しかしながら，コンピュータ性能の発展により，計算量を必要とする手軽な最適化手法がより身近になったことが，新たな非線形解析技術の提案につながったのである．こういった新技術を，AUTO⁽⁵⁾やBunKi⁽⁶⁾に代表されるような分岐解析ソフトウェア化ができれば，これまで非線形解析になじみのなかった分野でも積極的に利用されることが期待でき，それにより，新たな技術の発見につながるであろう．それでは，非線形解析技術の発展がもたらす未来を考えてみよう．

　例えば，ロボット等の機械技術分野において非線形解析技術を用いた場合，パラメータに依存するシステムの解析が緻密かつ簡単にできるようになり，製品の開発速度がアップし，性能も向上し，また，コストダウンも期待できる．言わずもがな，ロボットの応用先は多岐にわたっているので，きっと私たちの生活の利便性を高めてくれることであろう．100年後は各世帯幾つもの生活補助ロボットを所有する時代になっているに違いない．

　また，脳内のニューロンの挙動をはじめとする神経モデル系では，現在でも積極的に非線形解析が行われている．また，遺伝子の相互関係や代謝の仕組みをモデル化した生体システム系の解析も進められている．これら分野においても，高次元の分岐解析が一気に簡単にできるようになるとすると，制御可能なパラメータを増やすことができることから，より複雑な生体システム系の数理モデルの構築，及びその高精度な解析が期待できる．これにより，ニューロンの振舞いやシナプスの役割の解明等の発展につながり，人間の脳構造をより忠実に模倣した人工知能やコンピュータが開発されたり，これまで原因不明とされていた様々な病因が解き明かされたりするのではないだろうか．

　一方近年，ディープラーニングによる高度な画像認識や音声認識が話題になっているが，この技術が要する計算量は膨大であり，昨今の計算機性能の向上をもってしても学習に多くの時間を必要とする．対して，非線形素子を含む電気回路においては，パラメータ（回路素子）の値を少し変更するだけで，回路の結合関係を変更することなく，元の回路は簡素であるにもかかわらず，複雑かつバラエティに富んだ現象を観測できることが知られている．非線形回路におけるこれらのカオス現象や同期現象に関する研究も，長年にわたって多くの研究者によって行われてきた．非線形解析が発展し身近な存在となれば，これらカオス回路がロボットの脳等に利用され，さほど大きな計算機性能を要しないにもかかわらず，より人間に近い複雑な振舞いを行うロボットの開発ができたりするのではないだろうか．1980年代後半にニューロ・ファジィ洗濯機が発売され話題になったが，洗濯物の汚れ度合いに応じて回転のカオス度が変化するカオス洗濯機ができているに違いない．

　また，非線形時系列解析が発展すれば，地震や気象現象，株価等といった複雑な非線形現象の予測精度が格段に上がるかもしれない．個人の行動予測も簡単かつ高精度にできるようになれば，行方不明者や逃亡した犯罪者の発見が容易になることが期待できる．また，SARSやMERSといった私たちの命を脅かす感染症の伝播のモデル化，解明，予測ができれば，被害を最小限に抑えることに貢献するであろう．これにより，これまでなかなか防ぐことのできなかった突然の自然の猛威に対して，より柔軟かつ堅ろうな対応ができるようになると考える．

　これらのように，非線形解析の応用による様々な分野の発展の可能性は無限大である．もちろん，実社会につながる応用研究ばかりがもてはやされることを望むわけではないが，これまで分野外の人にはなじみが薄かった“分岐”や“カオス”といった単語が日常的にテレビで聞かれる日が来るならば，それをうれしく感じるのも非線形に関わる研究者の端くれとしての正直な気持ちである．

4．お　わ　り　に

　筆者らが考案した，メタヒューリスティックな手法を用いた手軽かつ高精度な非線形解析手法を紹介させて頂いた．また，非線形解析の発展とそれがもたらす未来予想について楽観的かつ無責任に述べさせて頂いた．

　実は，この原稿の執筆依頼を頂くまで，筆者は来年のことさえ具体的に考えたことがなかった．それなのに，100年後の構想を練りなさいというわけであるから，正直なところ大変難儀した．自身のこれからの研究活動についてじっくりと考える貴重な機会を与えて頂いたことに心より感謝申し上げる．

　しかしながら，結局は目の前にある課題や謎を少しずつ解き明かしていくことが，未来へつながる第一歩なのであろう．これからも研究会や国際会議に積極的に参加して成果を発表し，様々な方々との出会いやつながりを大切にしつつ，これらの未来の実現に少しでも貢献できるように，日々精進して研究に励んでいきたい所存である．

文　　　　　献

(１) H. Matsushita and T. Saito, “Application of particle swarm optimization to parameter search in dynamical systems,” NOLTA, vol.2, no.4, pp.458-471, Oct. 2011.

(２) Y. Tanji, H. Matsushita, and H. Sekiya, “Particle swarm optimization for design of class-E amplifier,” NOLTA, vol.3, no.4, pp.586-595, Oct. 2012.

(３) J. Kennedy and R.C. Eberhart, “Particle swarm optimization,” Proc. IEEE Int. Joint Conf. on Neural Netw., pp.1942-1948, 1995.

(４) H. Matsushita, Y. Tomimura, H. Kurokawa, and T. Kousaka, “Period doubling bifurcation point detection strategy with nested layer particle swarm optimization,” Int. J. Bifurcation Chaos (印刷中).

(５) E. Doedel and B.E. Oldeman, 2012, http://indy.cs.concordia.ca/auto/

(６) ERATO, JST, 2004, http://bunki.ait.tokushima-u.ac.jp:50080/

　（平成28年12月28日受付　平成29年1月27日最終受付）

images/fig_3.png