1．圧縮センシング
――新しい圧縮技術――

　私たちが普段スマートフォンなどのディジタル機器を用いて視聴している音楽や映像のほとんどは，原信号を圧縮したものを，再び人間が認識できる信号に戻す処理を行った結果として得られたものである．原信号を圧縮する処理は（情報源）符号化，戻す処理は復号と呼ばれる（図1(a)）．このような処理を行うことで，ユーザは高品質な作品をスムーズに視聴することが，通信会社は自社の回線を効率的に使用することが可能になる．

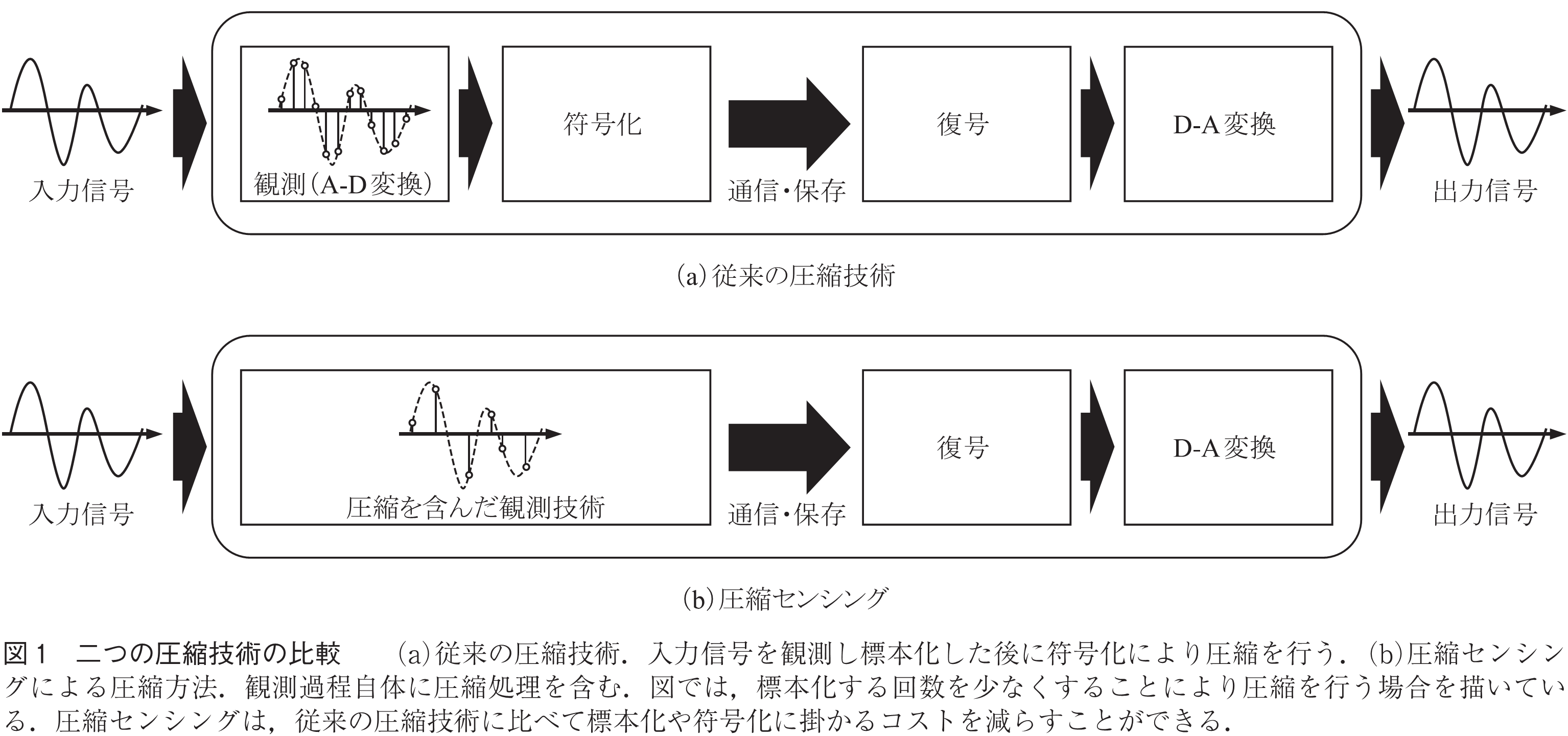
　ところで現在用いられている圧縮技術のほとんどは，標本化定理に基づく観測を行うことで得られた信号に対して適用される．音や映像などの興味のある対象をマイクロホンやカメラなどで余すところなく観測し，これによって得られた信号を人間の聴覚や視覚の特徴に基づいて，あるいは冗長性を利用することで圧縮を行うのである．しかし，そもそも圧縮することを前提とするのであれば，始めから満遍なく観測しなくてもよいではないだろうか．このような疑問に対する答えの一つが2006年頃にDonohoの論文⁽¹⁾で提唱された圧縮センシング（compressed sensing, compressive sensing）という技術である．

　圧縮センシングの観測過程は，興味のある信号をとして，

と表現される．ここで，は観測結果，は観測行列をそれぞれ表す．従来の圧縮技術のパラダイムでは，観測の際には信号を余すことなく取得する．これは式(１)において観測結果と原信号が1対1に対応するように，すなわちとなるように観測を行っていることとみなすことができる．一方で，圧縮センシングでは図1(b)のように観測と同時に圧縮を行ってしまうという考え方を採用する．このため，はよりも短いベクトル，すなわち，になるように観測を行う．このような観測過程を用いることで，従来の圧縮技術における標本化や符号化に掛かるコストを減らすことができるのである．

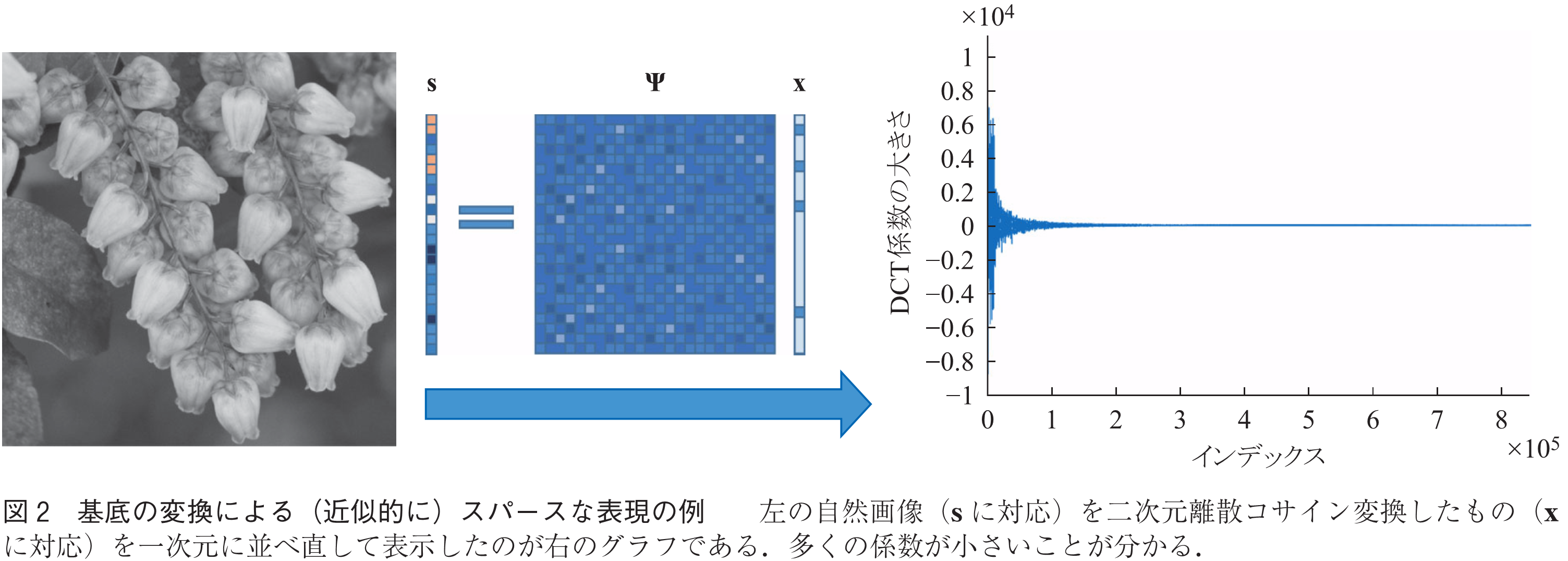
　さて，このようにして圧縮された信号をどのようにして復号すればよいだろうか．である場合はのため，から復号後の信号を一意に定めることはできない．そこで圧縮センシングの復号では，のにおける表現がスパース性，すなわちの要素のうち非零の値を持つ要素の数が要素全体の数に比べて小さいという性質（図2）を持っているだろうという先験情報を導入することで，この不足を補う．したがって，復号処理は観測過程(１)を満たすという条件の下で，スパース性が高いベクトルを探す問題を解くことによって行うことができる．

　興味深い問題の一つは，このような復号処理がどの程度の復元性能を持つか，すなわちどの程度まで観測数を減らして圧縮してしまっても元の信号を復元できるかということである．今，原信号が実際に個以下の非零要素を持つベクトルでのように表現できるとしよう．このとき，がの定数倍程度あれば非常に高い確率でひずみのない信号を現実的な計算量で実行可能な復号処理によって復元できることが知られている⁽²⁾．元々の方程式(１)を思い出すと未知の変数の数がであるにもかかわらず，の定数倍程度の条件によって正解を求めることができる，というのは驚くべきことである．一方で，非零要素の数は個しかないことから，必要な観測数を更に減らす余地もありそうだ．圧縮センシングの復号処理を行うための様々な方法が提案されており，かつそれらの持つ性能の多くが現在までに明らかにされてきた．

　圧縮センシングの拡張の一つである分散圧縮センシングは，複数の信号を同時に扱う場面で1チャネルのみを扱う圧縮センシングと比べて高い性能を持つと期待されている技術である⁽³⁾．音楽ではステレオ信号のように，映像であれば連続する複数枚の画像信号のように，よく似ている複数の信号を扱う必要が生じることがある．また，近年ではInternet of Things（IoT）のようにありとあらゆるものをインターネットに接続し，情報を収集，活用しようという動きが活発である．このような状況では，私たちが観測しようとしている複数の信号の間には何らかの関係性があることが期待できるだろう．ではこの関係性を使って，どの程度性能を上げることができるのだろうか．

　筆者らは最近，分散圧縮センシングの性能を確かめるために，二つの復号方法に関して情報統計力学と呼ばれる手法を用いて理論的な評価を行った⁽⁴⁾．この評価においては，複数チャネルの信号のモデルとして各チャネルの非零要素の位置が同じである結合スパース性と呼ばれる性質を満たす信号を対象とした．解析の結果，二つの方法のいずれについても，チャネルの数が増えると，復元性能が上がることが分かった．特に，ベイズ最適な方法と呼ばれる事前に信号の生成分布を知っているとした復号方法は，10チャネル程度の信号を同時に復号することで，1チャネル当りの観測数と非零要素の数が同じであるという最も難しい条件においても，ひずみのない信号を得られることを示唆する結果を得た．先行研究⁽⁵⁾やこれらの事実から，分散圧縮センシングには確かに通常の圧縮センシングを上回る復元性能を持つことが分かる．

　ここまでは，圧縮センシングとその複数チャネル環境への拡張版である分散圧縮センシングについて，主に圧縮の性能に着目して述べてきた．圧縮センシングにおいて圧縮の性能が高いということは，その分観測に労力を掛けなくてもよいということを意味している．2．と3．では，この観点からこの圧縮と観測技術が活躍する未来の姿と課題を記す．4．では，少し違った視点から圧縮センシングの枠組みについて考察し，私たちの物事の捉え方のモデルとして役立つ可能性について考察する．これらを通して，圧縮センシングが私たちの将来を考える上で重要な技術であることを少しでも伝えることを本稿の目標とする．

2．圧縮センシングの展開

　圧縮センシングは私たちにどのような恩恵をもたらすだろうか．MRI（Magnetic Resonance Imaging，核磁気共鳴映像法）などの医療イメージングは圧縮センシングが発表された当初から最も注目されてきた応用先の一つである⁽⁶⁾．これらの方法は，1枚の画像を取得するために複数回の観測を必要とする構造を持っており，時間的な意味での観測コストが高い．また，同じ理由で時間解像度を高めることが困難であるため時間変化を観察する上でネックとなっていた．観測の対象である生体の内部画像がスパースであることを利用しようというものから，時間と空間構造の両方を考慮したダイナミックMRI向けのものまで様々な研究がなされており，早期の実用化が期待されている．

　医療イメージングに加えて，最新の電波天文学の分野でも圧縮センシングは注目を集めている．電波望遠鏡を使った観測では，望遠鏡のペアを用いて実効的な解像度を上げる開口合成と呼ばれる方法が用いられている．より正確な像を得るためには，なるべくたくさんの望遠鏡を用意し，様々な組合せで観測を行うことが望ましい．ところが，その設置コストの高さから実際には十分な観測を行うことが困難であることが多い．これを解決するため，特にブラックホールの観測に圧縮センシングを応用した研究が進められており，理論的な予想が証明される日も近いと期待されている⁽⁷⁾．このように，医療という身近なところから最先端の科学研究まで，圧縮センシングは私たちが今まで見ることのできなかった世界を観測する技術として活躍する可能性を持っている．

3．分散圧縮センシングの課題

　産業界を中心にIoTが普及しつつあり，今後もますますその重要性が高まっていくだろう．地球環境のモニタリングをより幅広くかつ詳細に行うことで変化の前兆をより早く捉えることができるかも知れない．より低コストでエネルギー消費が小さい観測技術が果たす役割は大きいだろう．ここでは，分散圧縮センシングがこの分野に貢献するための課題について述べる．

　分散圧縮センシングの性能向上はより実際の信号に近いモデルを見つけられるかどうか，という点に掛かっている．前章で取り上げた結合スパース性はやや強い仮定であり，実信号にこれを直接適用することは難しい．このため，より現実の信号が持つ構造に近いチャネル間の相関を表すために信号モデルが提案されており，各々の特徴を満たす信号に対して圧縮性能が上がることが示されている⁽⁸⁾．また，信号が持つ構造をあらかじめ定めてしまうのではなく，復号の過程で複数チャネル間の相関を推定しようという試みもなされている^(9)～(11)．筆者らも，実際の生体信号についてこのような方法を提案し，固定的な構造を仮定したモデルを用いる場合に比べて復元性能が上がることを示した⁽¹²⁾．複数の信号の間に存在する関係を推定する方法は，分散圧縮センシングの文脈に限らず，複数のカメラを用いた超解像技術などの分野でも活発に研究されている⁽¹³⁾．これらの知見を取り入れながら，より現実に近い信号モデルを発見あるいは推定する方法の確立が期待される．

　分散圧縮センシングを実環境に適用するにあたって，もう一つの重要な課題となるのは性能保証の問題である．少なくとも，複数の信号の間の相関を仮定した復元方法が，通常の圧縮センシングによる復元性能を下回らないことを示す必要があるだろう．筆者らが結合スパース性を持つ場合を扱ったように，幾つかの場合についてはあらかじめどのような復元性能が期待できるのか知ることができる．しかしながら，信号間の相関を復号過程で推定する方法の性能を理論的に保証することは一般には困難である．これは，主に信号そのものと信号間の相関という二つの未知の変数を同時に推定しなければならないという構造に起因するものである．これらの問題は理論的にもチャレンジングであり，今後も取り組んでいくべきであろう．

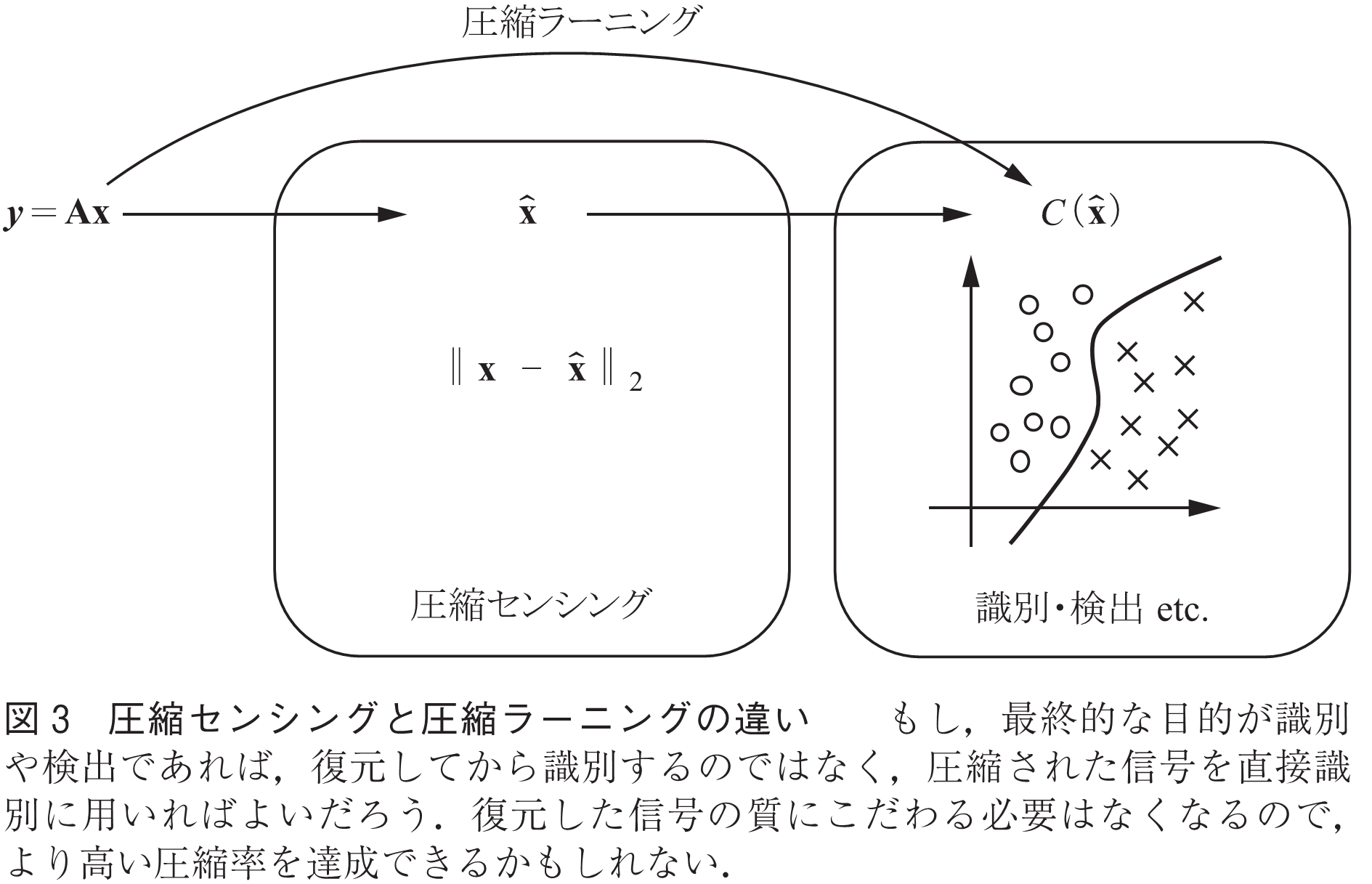
　分散圧縮センシングの今後を考える上で，近年著しい発展を続ける機械学習分野との関係に言及する．私たちがたくさんの情報を集めるのは，機械を対象にしていれば故障の有無，環境のモニタリングであれば変化の予兆というように元の信号から推定される何らかの知見を得るため，ということが多い．このような視点から，「どうせ圧縮してしまうなら最初から真面目に観測しなくてよい」というパラダイムから更に「どうせ識別するだけならもっと不真面目な観測でよい」という段階まで進めた圧縮ラーニングの研究が行われている^(14),(15)（図3）．この考え方と，分散圧縮センシングの考え方を合わせることができれば，目的に対して必要最小限の観測を行うシステムの構築が可能になるだろう．

　分散圧縮センシングも圧縮センシングと同様に私たちの目の届かなかった範囲に光を当てることを可能にする技術である．ここで挙げた課題を解決し限りあるエネルギー資源や電波資源を最大限に活用することが可能になれば，地球や宇宙における大規模な常時観測が実現し，より安心で安全な社会を実現できるのではないだろうか．

4．私たちと圧縮センシング

　シャノンが「通信の数学的理論⁽¹⁶⁾」で提示した通信路のモデルは電気通信分野のみならず，人間同士のコミュニケーションまで含めた広い意味での情報伝達に関する学問に影響を与えた．圧縮センシングも圧縮や観測の技術としてだけではなく，人間の物事の捉え方についてのモデルとして解釈することはできないだろうか．これを正当化できれば，圧縮センシングによって私たちの行動を予測することができるかもしれない．

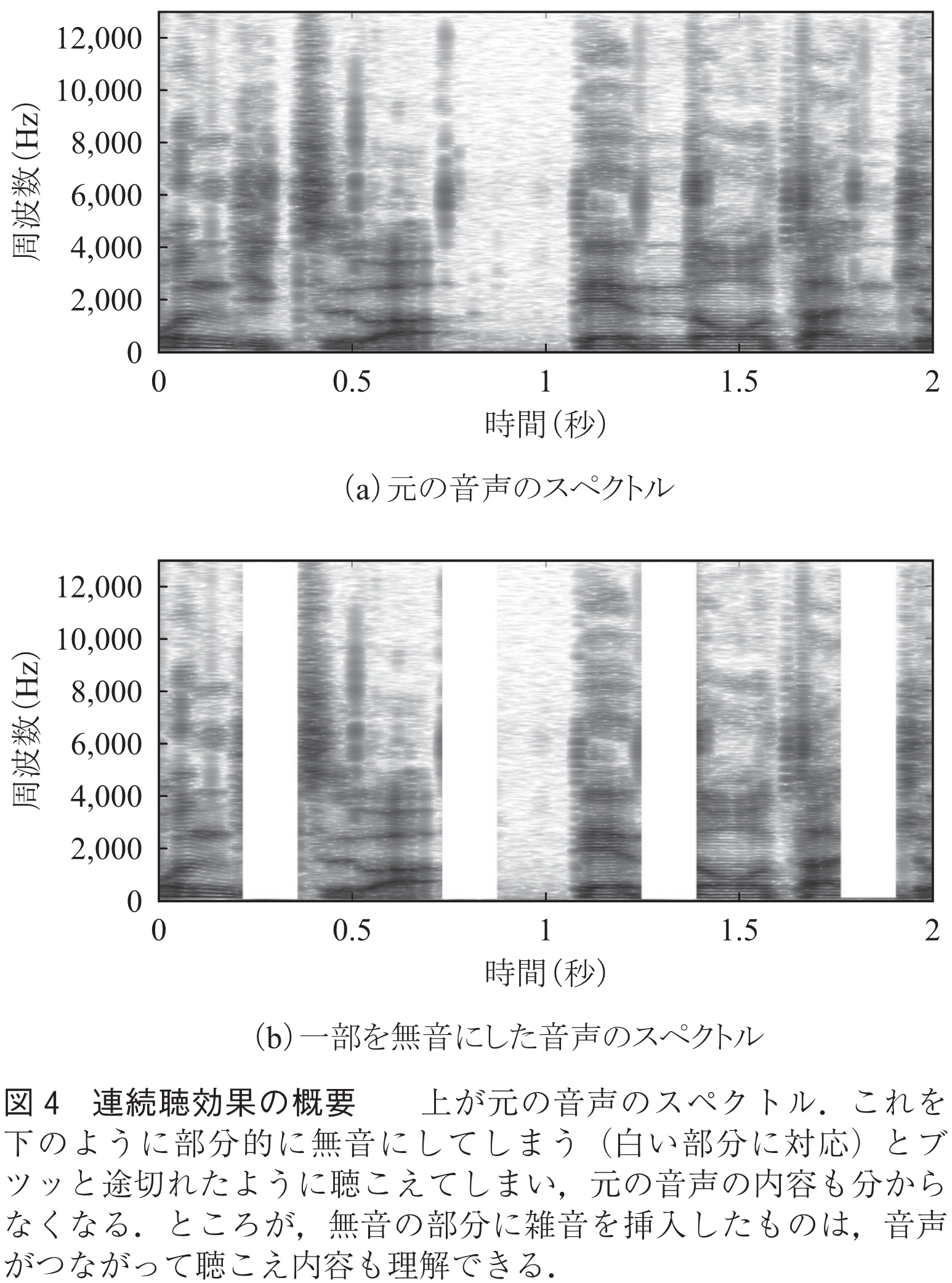
　例えば，連続聴効果と呼ばれる聴覚に関するよく知られた錯覚がある⁽¹⁷⁾（図4）．ある文を読み上げた音声を収録したものを一定間隔で切り取って無音にしたものを聴くと，ブツッブツッと途切れてしまうために何を言っているのかよく分からない．しかしながら，無音の区間に雑音を入れることで今度は連続した音のように聴こえるようになり，読み上げている文の内容も分かるようになる．このような錯覚は，声だけでなく音楽についても起こり，更に視覚についても同様の錯覚が知られている（文献(18)で体験することができる）．この錯覚の重要な点は，雑音があることによって「本来そこにあるべき音声が隠されてしまった」と勘違いし，実際には存在しなかった音を補完して知覚してしまう，というところである．このことを圧縮センシングの立場から素朴に見ると，「隠されてしまった」と勘違いした区間が失われるような観測過程を用いて圧縮を行い，その観測結果と何らかの先験情報を元に音を復元して知覚しているのではないか，と考えたくなる．これは現時点では単なるアナロジーに過ぎないが，人間の知覚を理解し，その振舞いを予測する上で何らかのヒントになるかもしれない．

　連続聴効果は雑音中の音を聴き取る上で重要な役割を果たしているとされ，上記の例⁽¹⁸⁾でも実際に「正しい」音声を聴き取ることができるはずだ．これは，私たちが持つ先験情報が自然な音にうまくチューニングされているためだろう．一方で，このような補完が常に良い結果をもたらすとは限らないだろう．日常の会話ではある種の先験情報を用いて省略された内容を補う必要があるが，そこには読み違いのリスクが付きまとう．お互いの持つ文脈が異なる，と言われるようなこういった状況は先験情報の食い違いとして表現できるかもしれない．このように補完とリスクの関係も圧縮センシングの立場からモデル化することができれば，トラブルを未然に防いだり，どの程度の問題が生じるかをあらかじめ知ることができるだろう．

5．む　　す　　び

　私たちが生きていく上で，どのような危機が迫っているかをあらかじめ知っておくことは，それを未然に防いだり対策を練ることを可能にするという意味で重要である．このような予測を行うためには，より広範囲にわたる観測と正確なモデリングが欠かせない．本稿で述べたように，圧縮センシングは，私たちの観測可能な範囲を広げることを可能にする技術である．この技術を発展させることで，目の届かない範囲をなるべく小さくしたい，というのが筆者の願いである．また，圧縮センシングのようなものの見方は私たち人間の行動を予測するモデルとしても活用できるかもしれない，と筆者は考えている．私たちは常に不完全な情報に基づいて判断し，行動することを迫られている．このような状況でもなるべく悲劇が起きないようにするためには，もっと私たち自身についても知る必要があるだろう．地球や宇宙が平和であるために，圧縮センシングが少しでも役に立ち，また筆者自身がその一助となることができれば幸いである．

文　　　　　献