
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|
オリンピック,パラリンピック,そして
小特集 4.
「個と群」
――アート・サイエンス協働教育――
“Individual and Group”: Education through Art and Science Collaboration
abstract
東京大学教養学部では,2019年2月に美術家の野老朝雄と東京大学の舘知宏によるアート・サイエンス協働の集中講義「個と群―紋様デザイン」を開講した.野老は東京2020オリンピック・パラリンピックエンブレムの「組市松紋」をはじめとして,幾何学的操作や原理に基づき多様な表現・デザインを生み出してきた.文理を含む全科類の学部1,2年生が受講し,実作とその講評を通して幾何学的原理から各自の芸術表現へと展開することが課せられた.形を介してつながる諸科学現象や幾何学原理についても同時に学び,制作へと反映させた.教育の取組みと協働により生まれた研究成果などを紹介する.
キーワード:非周期タイル,アート・サイエンス協働,幾何学
野老朝雄は東京2020オリンピック・パラリンピックエンブレムの「組市松紋」をはじめとして,幾何学的操作や原理に基づき形状をつなげていくことで多様な美術表現を生み出している.黄金比列を半径とする円の集合による平面構成(Kumapon-g),正方形,正三角形上に円弧の集合で描かれたしま模様を平面敷き詰めするシステム(PPP),四角形の板を帯状に接続して生まれる変形可能なスポンジ状の空間構成(Build Void)などがある.野老はこれらの創作の一連のプロセスを,単純な形状「個」が幾何学的接続のルール「律」に従って組み合わさることで「群」をなすことから,「個と群」あるいは「個と群と律」と表現している.
野老の活動の特色の一つは,作品の創られる原理の共有と,その共有を通した諸領域との協働である.2017年の「野老朝雄展 CONNECT」では,漆作家,建築家,藍染め作家,数学者,工学者,科学者など,10名以上のコラボレーターたちそれぞれとの作品を展示するというスタイルで開催された.ここでは3Dプリンティングやレーザ加工などのディジタルファブリケーション技術で新しい美術表現が可能になったり,作品から数学上の問題に展開したりと,双方向のアート・サイエンス協働を醸成している.舘知宏は,野老の「組市松紋」を変形メカニズムである剛体折紙として解釈した「剛体折紙組市松紋様」をCONNECTの中で展示している.これは,パターンの変形によって新しい機能性を得る「機械的メタマテリアル」と呼ばれる近年ホットになっているサイエンスのトピックともつながっている.
作品の背後に存在する幾何学と関連する諸領域について,2020東京オリンピック・パラリンピックエンブレム「組市松紋」を例として取り上げる.組市松紋を構成する3種類の藍色の長方形は,図1(a)に示す30°(と150°)のひし形,60°(と120°)のひし形,90°のひし形(正方形)それぞれの辺の中点を結ぶことで得られる.
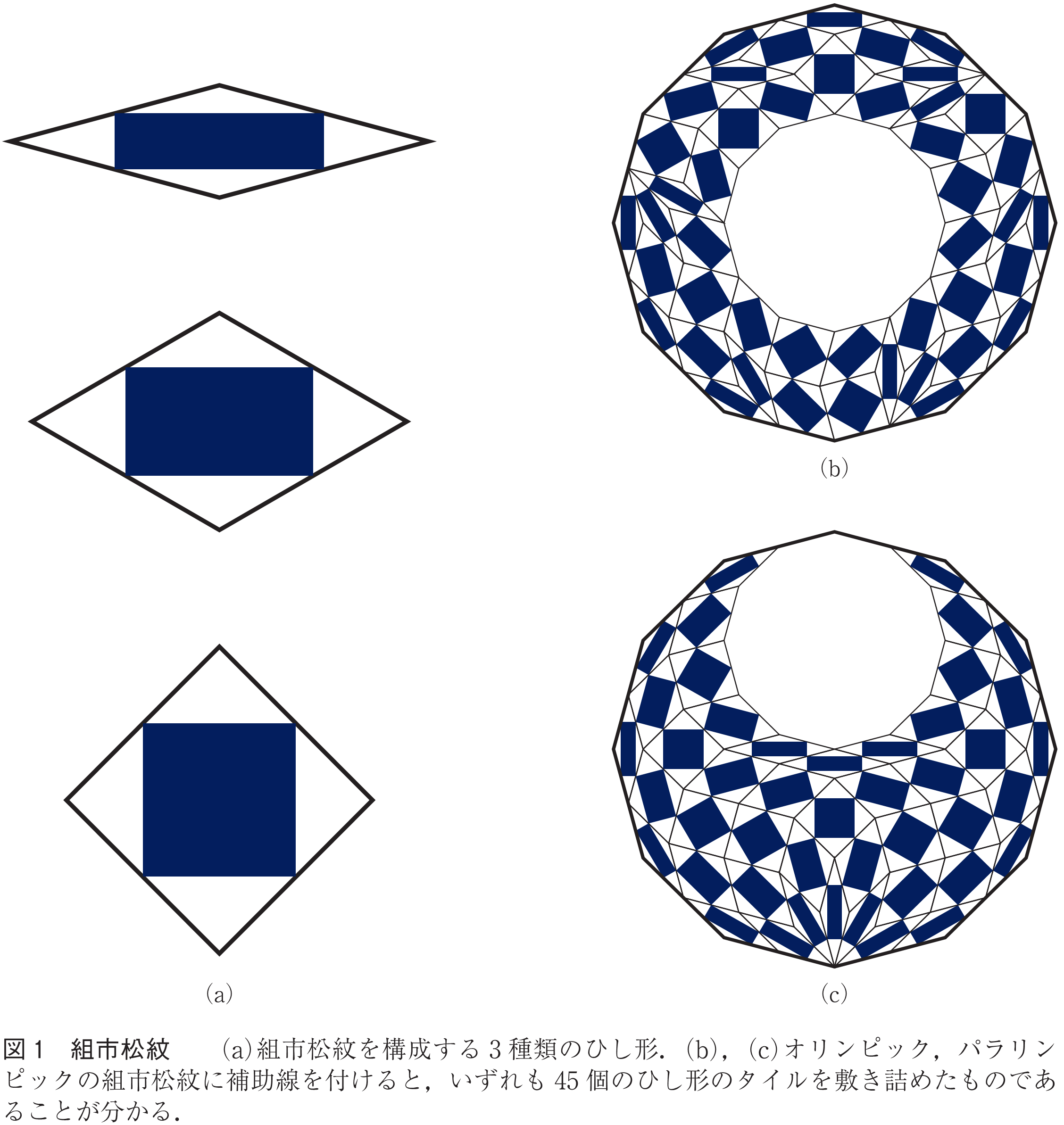
図1(b),(c)は,ひし形のタイルが分かるように組市松紋それぞれに補助線を引いたものである.どちらも外枠に大きな正十二角形,内枠に小さな正十二角形があり,その外枠と内枠の間に,枠からはみ出さないように3種類のひし形45個が敷き詰められている.また,どの二つのひし形のタイルも,頂点や辺を共有して隣接することはあっても,面的な重なりは持たない.より詳しく見ると,敷き詰め(タイリング(用語))において,正十二角形の辺の傾き6種類のうちのどの二つのペアにも,それと同じ辺の傾きを持つひし形のタイルが三つずつあり,その敷き詰め方を変えることで,オリンピックの紋にもパラリンピックの紋にもなることが分かる.
エンブレムの補助線のひし形のタイルの多様性は,ペンローズタイルなどに代表される非周期的なタイリングと同じ仕組みであることが分かる.ペンローズタイルでは36°と72°を用いたひし形が無限に平面を充塡する.このような非周期タイルはまた,自然界では準結晶の幾何学に現れる.ノーベル化学賞を受賞したダニエル・シェヒトマンは5回対称性を持つ「結晶」を発見したが,この構造は三次元空間中の2種類のひし形六面体による非周期タイルによって説明される.
オリンピック・パラリンピックエンブレムは,無限のタイリングではなく,有限の十二角形内に3種類のひし形を収めている.無限ではなく有限であるので,その組み方のバリエーションも有限となるはずである.このような問題ではアルゴリズムを用いた列挙(用語)によってその全貌が見えてくる.
正十二角形の外枠と内枠の間に3種類のひし形45個を敷き詰めたタイリングは,オリンピックとパラリンピックの組市松紋のほかにも考えられる.では,そうしたタイリングは,何種類あるのだろうか? 濱中裕明,堀山貴史,上原隆平は,以下のようなアプローチ(1)で,全てのタイリングを列挙した.
図2(a)は,正十二角形の外枠と内枠の間に3種類のひし形タイル60個を敷き詰めたタイリングであり,ひし形の向かい合う平行な辺の中点同士を結ぶように線分を描画したものである.隣り合うひし形の線分は,折れ曲がりつつもつながっており,ひし形10個の平行な辺を順に通るひも(pseudoline)を構成している.図2(a)では,12本のひもが,外枠の正十二角形の右半分の辺から出て向かい合う左半分の辺に至ることが見て取れる.このひもの交差それぞれがひし形のタイルに対応し,12本のひもがどのような順番で交差するかでタイリングが決まる.(ここでは,交差する2本のひもの上下は考えない.)

図2(b)は,12本のひもの交差を「あみだくじ(用語)」として表したものである.それぞれのひもの両端点のうち,右半分の端点をあみだくじの上側に,左半分の端点を下側に配置している.また,2本のひもの交差を,あみだくじの2本の縦線を結ぶ横棒で表している.こうして,タイリング,ひもの交差,あみだくじの間に1対1の対応関係が定められる.
オリンピックやパラリンピックの組市松紋には,内枠の小さい正十二角形が穴のように開いている.この正十二角形をタイリングのタイルの一つとみなし,ひし形と同様に,向かい合う6組の辺の中点同士を結ぶと,タイリングをやはり12本のひもの交差に対応付けられる.更に,あみだくじでも正十二角形の部分を扱うために,縦線6本を結ぶ1本の特殊な横棒を導入し,この横棒では左右の順を全部まとめて反転させる.これにより,穴の開いたタイリングも扱うことができるようになる.オリンピックやパラリンピックのように穴が真ん中や一番上の位置にあるタイリングについて,それぞれ53万9,968通りと335万7,270通りの敷き詰め方を列挙し,それぞれ何通りあるかを確定した.
2019年2月に野老と舘によるアート・サイエンス協働の集中講義「個と群―紋様デザイン」が東京大学教養学部において開講された.文理を含む全科類の学部1,2年生を中心に20名弱が受講し,実作とその講評を通して幾何学的原理から各自の美術表現へと展開することが課せられた.ガイダンスと最終講評会を含めて全6回の構成であった.
2018年11月のガイダンスでは野老によるレクチャー「個と群と律」により,2020エンブレムの成り立ちを含めてその作品の創られる原理が共有されたのち,「30°60°90°を使って作品を制作せよ」という出題があった.2019年2月からは,毎週約5時間全4回分の集中講義が行われた.集中講義では学生が制作した彫刻物,映像作品,インタラクティブ作品などに対して,野老と舘から美術,科学,建築など領域を横断したコメントを行い,次の制作にフィードバックさせた.
また,野老と協働する諸領域の研究者がゲストレクチャーとして登壇した.堀山貴史は組市松紋のひし形のタイリングの列挙や等価なモデルに関する最新研究成果について,荒木義明は敷き詰め(テセレーション(用語))の数理とデザインについて,エッシャーの作品との関連を含めて,また鳴川肇は四面体の展開図が平面を埋め尽くせることを利用した新しい地球の投影法「オーサグラフ(Authagraph)」について,松川昌平はエンブレムの幾何学の組合せと平面上の直線の交点のシークエンスとを関連付ける手法について講義を行い,手掛けた「東京2020 NIPPONフェスティバル」の映像作品を紹介した.
最終講評会は東京大学教養学部内の駒場博物館にて行い,学生は効果的な展示の仕方についても検討をした.
受講した学生の意欲は高く,幾つかの作品はその後も継続して共同研究へと展開している.その現状を報告する.
割鞘奏太(当時学部1年)は,オリンピック・パラリンピックの組市松紋を三次元に拡張した.二次元においては,3種類のひし形のタイルによって十二角形を分割したグリッドに基づき,それぞれのひし形の中点で点接続された長方形群を作ることで紋としている.割鞘の作品は2種類の黄金ひし形六面体によってひし形三十面体を充塡し,それぞれの六面体の双対となる八面体を挿入する操作により,頂点で接続された立体紋を完成させた.なお,この構造は立体トーラスとしても安定性があり構造合理性のある形状であり,空間構造の研究として発展継続中である(図3).

西本清里(当時学部3年)は,正三角形を構成要素として四面体とそのバリエーションを構成した.四面体の稜線と三角形分割が一致しないような四面体の三角形分割折りのバリエーションを得た.これらのバリエーションを二つの非負整数の組で表せることを示し,また四面体の性質から測地線に沿って三角形の帯を巡っていくと,四面体が幾つかの帯に分割できることが分かった.この帯の数は二つの整数の最大公約数であることなど,その後の共同研究へと発展している(2)(図4).

増渕健太(当時学部2年)は,多角形と音楽の平均律を関連付けて作曲・演奏のシステムを構築した.具体的には二十四角形中に6種類のひし形を埋め込むことで,12種類の方向の稜線で構築されたひし形分割を構成した.12種類の稜線の傾きを12平均律に対応させることで,ひし形を2和音,ひし形三つによる六角形を3和音として表現したり,音階を示す平行多角形を構築するといったインタラクティブな可視化のシステムを実装した.これらはアート展示として国際会議発表をしている(3)(図5).

本授業の中で教えることを通じて,学生との協働だけではなく,教員同士の共同研究にもつながった.堀山による列挙手法の講義からディスカッションを継続した結果,組市松紋のタイリングの列挙問題を次元格子から
次元空間への投影として捉えることを使った新しい数え上げ手法へと発展している(4).
本授業の取組みは東京大学に2019年に発足した「東京大学芸術創造連携研究機構」の構想に基づいて実現した.2019年度(2020年2月)も継続しており,更なる新しい展開が継続中である.機構が開講する授業では,芸術の実技・制作・発表に取り組むことで,これまで学生が東京大学で触れてきた科目とは大幅に異なる多様な思考や創造のプロセスを獲得し,知性を拡張することを目指している.本講義では,そのような取組みに加えて,更に芸術家と科学者が協働しながら授業を行う形式とした.これにより,教室をアートとサイエンスのコラボレーションの現場とすることを目指した.
現在の科学の最先端は,分野を横断する複合的あるいは境界的な領域にある.ここでは,異なる背景を持つ専門家が共通の強い興味を持って協力してコミュニケーションを図る必要がある.異分野のディスカッションは,各コントリビュータが専門領域に閉じず,たびたび相手に対して基本に立ち返った専門のレクチャーを行う必要が生じる.また議論の共通基盤となる「言語」のようなものが必要である.今回の授業では,基本に立ち返ったレクチャーはまだ専門分野の教育を受けていない教養課程の学生にとっても(チャレンジングであるが)理解できる内容となったと考えている.また実際に手を動かして「かたち」を作ることで,その背後の幾何学が共通言語として共有されたのではないかと考えている.そのため,教える側と教わる側という一方通行ではなく,教養課程の学生であっても,教員と協働してすぐに研究のプレーヤとして最先端の問題に取り組めることにつながったと評価している.
(1) H. Hamanaka, T. Horiyama, and R. Uehara, “On the enumeration of chequered tilings in polygons,” Bridges 2017 conference, pp.423-426, Waterloo, Canada, July 2017.
(2) S. Nishimoto, T. Horiyama, and T. Tachi, “Geodesic folding of tetrahedron,” Symmetry: Art and Science, Kanazawa, Japan, Nov. 2019.
(3) K. Masubuchi, A. Tokolo, and T. Tachi, “Rhombus tiling in icositetragon and twelve-tone emperament,” Symmetry: Art and Science, Kanazawa, Japan, Nov. 2019.
(4) T. Horiyama, T. Tachi, and A. Tokolo, “Another representation of rhombus tilings,” The 22nd Japan Conference on Discrete and Computational Geometry, Graphs and Games, pp.73-74, Tokyo, Japan, Sept. 2019.
(2020年3月5日受付 2020年3月12日最終受付)
■ 用 語 解 説
オープンアクセス以外の記事を読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード