Vol.104 No.10 (2021/10)　目次へ

解説

トポロジー最適化の理論と様々な物理問題への展開事例

A Theory of Topology Optimization and Its Applications to Various Physics Problems

西脇眞二

西脇眞二　京都大学大学院工学研究科機械理工学専攻

Shinji NISHIWAKI, Nonmember (Graduate School of Engineering, Kyoto University, Kyoto-shi, 615-8540 Japan).

電子情報通信学会誌　Vol.104 No.10 pp.1098-1104 2021年10月

　本記事の著作権は著者に帰属します．

A bstract

　トポロジー最適化は，形状変更に加え穴の数の増減などの形態の変更をも可能とする最も自由度の高い方法である．この方法により，高性能な最適構造が得られるだけではなく，新しい機能を持つ構造を創成することも可能である．本稿では，まずトポロジー最適化の基本的な考え方とその定式化及び実装方法を簡単に説明する．次にトポロジー最適化の様々な物理問題へ適用した事例を紹介する．すなわち，構造問題，流体問題，電磁気問題，音波・電磁波伝搬問題の適用事例を示し，トポロジー最適化の有用性・発展性を説明する．

キーワード：構造最適化，トポロジー最適化，有限要素法，均質化法，レベルセット法

1．ま　え　が　き

　構造最適化は，与えられた物理的条件と設計条件の下，指定した設計領域内において，力学的数値モデルと数学的な最適化の方法により，性能を最大限発揮できる形状構造を求める方法である．構造最適化は，寸法最適化，形状最適化，トポロジー最適化⁽¹⁾に分類され，この中で，トポロジー最適化は対象構造の形状のみでなく，穴の創成・消滅などのいわゆる形態の変更をも可能とする最も自由度の高い方法である．これにより，高性能な構造を得られるだけでなく，新しい機能を持つ構造を得ることができる．本稿では，トポロジー最適化の基本的な考え方とその定式化，実装方法を簡単に説明するとともに，トポロジー最適化の様々な物理問題へ適用した事例を紹介する．

2．トポロジー最適化の考え方

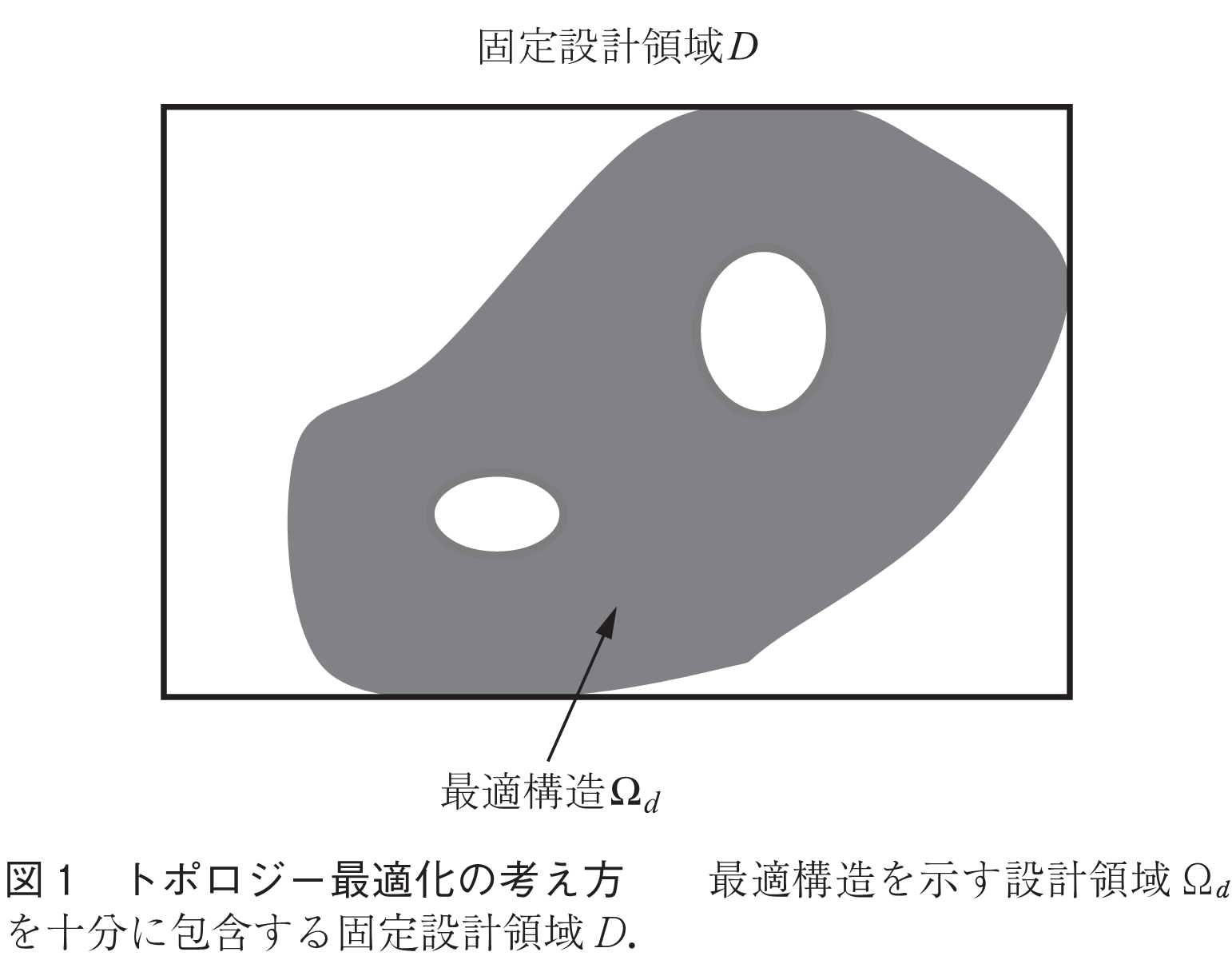
　トポロジー最適化の基本的な考え方⁽²⁾は，構造最適化問題を材料分布問題に置き換えることにある．すなわち，まず図1に示すように，求めるべき最適構造を示す設計領域 math を十分に包含する固定設計領域 math を設定する．そして，式(１)に示す特性関数 math により，固定設計領域内の適切な箇所に材料を配置させることにより最適構造を得る．この方法を用いれば，どのような形態・形状変更も可能とし，極めて設計自由度が高く，高性能な最適構造を求めることができる．

math

(１)

図1　トポロジー最適化の考え方

続きを読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。また、会員になると豊富な豪華特典が付いてきます。

続きを読む(PDF)　　　バックナンバーを購入する　　　　入会登録

電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。

電子情報通信学会誌会誌アプリのお知らせ

電子情報通信学会 - IEICE会誌アプリをダウンロード

解説 トポロジー最適化の理論と様々な物理問題への展開事例

1．ま え が き

2．トポロジー最適化の考え方

解説　トポロジー最適化の理論と様々な物理問題への展開事例

1．ま　え　が　き