
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

慣れない土地での移動は難しい.例えば車で移動するときには,カーナビゲーションが指示する交差点で曲がりそびれたりする.Uターンをして元の交差点まで戻らなければいけない.また,筆者は梅田の地下街でよく迷う.気がつけば同じ道を何度も行き来していることがある.国際学会などの旅先でも同様である.迷っている最中に意外な発見をすることもあるが,やはりそれでも無用な行き戻りは減らせるに越したことはない.
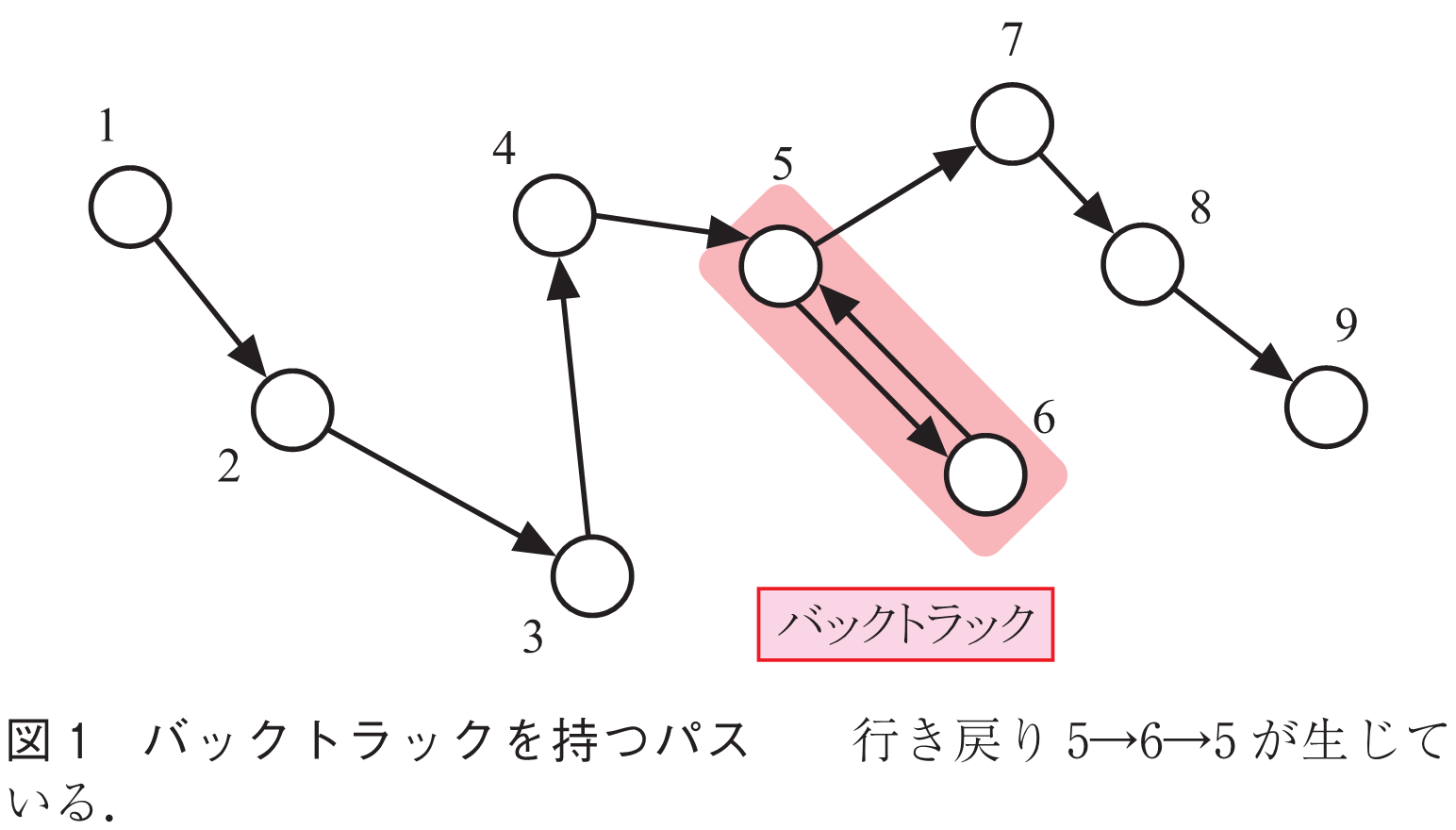
近年,ネットワーク解析においても行き戻り防止の有用性が注目されている.本稿ではバックトラックと呼ばれる行き戻りに焦点を当てる.大雑把に言うとバックトラックとは,図1に示すパスが含む行き戻り のことである.このようなバックトラックを防ぐことにより可能となるネットワーク解析を紹介したい.本稿ではネットワーク科学において代表的な研究テーマである酔歩,伝搬,中心性における以下の題材を扱う:
のことである.このようなバックトラックを防ぐことにより可能となるネットワーク解析を紹介したい.本稿ではネットワーク科学において代表的な研究テーマである酔歩,伝搬,中心性における以下の題材を扱う:
・バックトラックの禁止による酔歩の効率化(2.)
・非バックトラック性を考慮した感染症伝搬の漸近解析(4.)
・非バックトラック性の導入による中心性局在の緩和(5.)
また,途中の3.ではバックトラックを排除したネットワーク解析を行う際に便利な道具である非バックトラック行列を紹介する.
本稿で用いる記法と用語について述べる.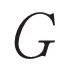 を
を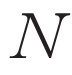 個の頂点
個の頂点 を持つ無向グラフとする.
を持つ無向グラフとする.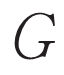 が持つ無向辺の数を
が持つ無向辺の数を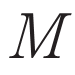 と書く.辺は重みを持たないと仮定する.また
と書く.辺は重みを持たないと仮定する.また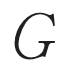 は連結である,つまり任意の二頂点の間にはパスが存在すると仮定する.隣接行列
は連結である,つまり任意の二頂点の間にはパスが存在すると仮定する.隣接行列 を
を
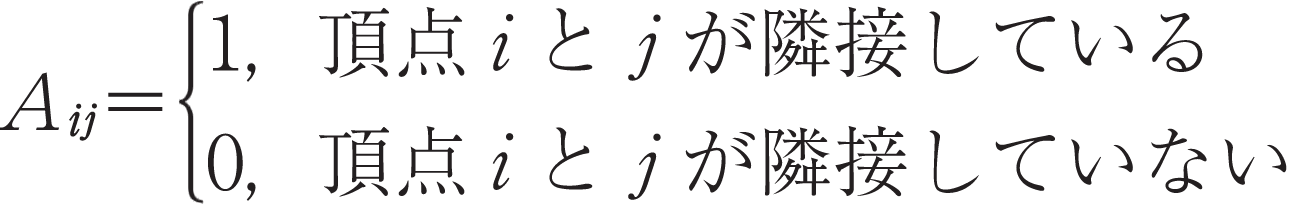
(1)
により定める.図2に無向グラフと隣接行列の例を示す.頂点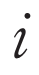 に隣接する頂点の集合を
に隣接する頂点の集合を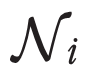 と書く.慣習と文脈に応じてグラフをネットワークと呼ぶことがあるが,意味に大きな違いはない.
と書く.慣習と文脈に応じてグラフをネットワークと呼ぶことがあるが,意味に大きな違いはない.
続きを読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード