Vol.105 No.12 (2022/12)　目次へ

CMOSインバーティブルロジック［Ⅱ］

――設計手法とツール――

CMOS Invertible Logic［Ⅱ］: Design Method and Tools

鬼沢直哉

鬼沢直哉　正員　東北大学電気通信研究所

Naoya ONIZAWA, Member (Research Institute of Electrical Communication, Tohoku University, Sendai-shi, 980-8577 Japan).

電子情報通信学会誌　Vol.105 No.12 pp.1458-1465 2022年12月

©電子情報通信学会2022

目　　　　次

［Ⅰ］確率的双方向計算手法の基礎（10月号）

［Ⅱ］設計手法とツール（12月号）

［Ⅲ・完］ハードウェア実現と応用例（1月号）

1．は　じ　め　に

　第1回で，双方向計算を既存のハードウェア上で実装可能なCMOSインバーティブルロジックの概要について説明を行った．典型例であるインバーティブルAND（IL-AND）ゲートを対象に，双方向計算を行う関数を表現するためのハミルトニアン係数と雑音制御による双方向計算の様子を紹介した．今回は，任意の関数に対するハミルトニアンの生成手法，及び自動設計ツールについて解説を行う．

2．任意の関数に対するハミルトニアン表現

2.1　線形計画法による小規模ハミルトニアンの係数生成手法

　ANDなどの論理ゲートのような小規模関数は，線形計画法により対応するハミルトニアン係数を決定することが可能である⁽¹⁾．ハミルトニアン（エネルギー）は前回も説明したとおり，

math

(１)

で定義される．ここでいうハミルトニアン係数とは math ， math であり， math はスピンの状態（－1 or ＋1）を表す．図1にIL-AND（ math ）のハミルトニアン係数の生成手順を示す．全部で8状態存在し，ANDの真理値表を満たす math ， math ， math の状態はValid，それ以外の状態はInvalidと定義される．

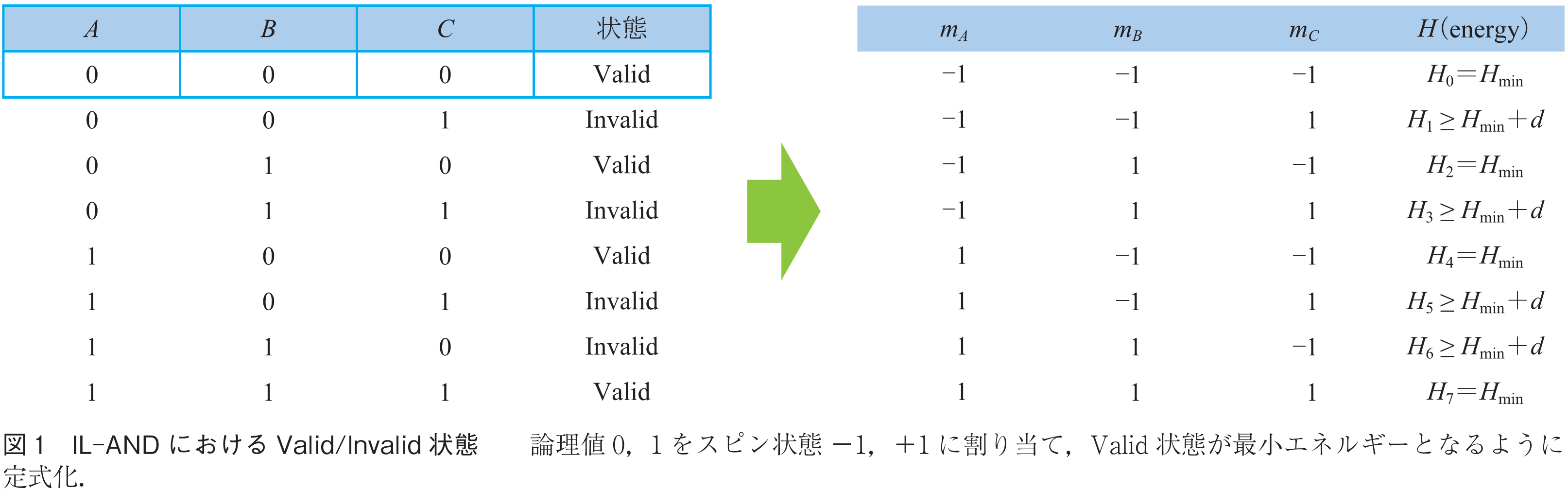
図1　IL-ANDにおけるValid/Invalid状態　　論理値0，1をスピン状態−1，+1に割り当て，Valid状態が最小エネルギーとなるように定式化．

　IL-ANDのハミルトニアン係数の生成方法について説明をする．まず，スピンの状態 math は－1と＋1を取るため，論理値‘0’をスピン状態 math ，論理値‘1’を math に変換する．次に，それぞれの状態におけるハミルトニアンを式(１)に基づいて定義する．インバーティブルロジックでは，Valid状態におけるハミルトニアンが最小（ math ）となり，Invalid状態におけるハミルトニアンがそれより大きい必要がある．そのため，任意の関数 math （ math は入力， math は出力を表し，それぞれ実数）に対して，Valid及びInvalid状態におけるハミルトニアン（ math ）は以下のように定義される．