Vol.105 No.2 (2022/2)　目次へ

システム数理の現状と展望

小特集 1.

ペトリネットの理論と応用

Application and Theory of Petri Nets

宮本俊幸

宮本俊幸　正員：シニア会員　大阪大学大学院工学研究科電気電子情報通信工学専攻

Toshiyuki MIYAMOTO, Senior Member (Graduate School of Engineering, Osaka University, Suita-shi, 565-0871 Japan).

電子情報通信学会誌　Vol.105 No.2 pp.106-112 2022年2月

©電子情報通信学会2022

Abstract

　離散事象システム・並行システムのモデル化言語の一つであるペトリネットは，1962年にカール・アダム・ペトリによって導入されて以来，様々な理論及び応用研究がなされてきた．例えば統一モデリング言語のアクティビティ図がペトリネットをベースにするなど，様々な分野で活用されている．ペトリネットのモデル化能力の拡張またはモデルの容易さのために様々な拡張が提案されている．本稿では，基本的なペトリネットを定義した後に，拡張ペトリネット及びその応用に関して解説する．

キーワード：ペトリネット，離散システム，ハイブリッドシステム

1．は　じ　め　に

　事象の離散的な生起によって状態が遷移するシステムは離散事象システムと呼ばれる．事象の生起に並行性があることから並行システム（コンカレントシステム）とも呼ばれる．通信システム，生産システムなど様々なシステムを離散事象システムとして見ることができる．本稿では，離散事象システムのモデル化言語であるペトリネットの理論と応用について解説する．

　まず，システムの分類について整理しておく（図1）．状態及び出力が，現在の状態と入力によって決まるシステムを動的（ダイナミカル）システムという．前文の「現在の状態と入力」は「現在までの入力列」と言い換えることができる．特に，出力が現在の入力のみによって決まるシステムを静的システムという．動的システムにおいて，入出力や状態変数が取り得る値の集合（状態空間）が連続集合のみで与えられるシステムを連続システムといい，離散集合のみで与えられるシステムを離散システムといい，連続集合と離散集合で与えられるシステムをハイブリッドシステムという．ハイブリッドシステムの理論と応用については本小特集2を参照されたい．

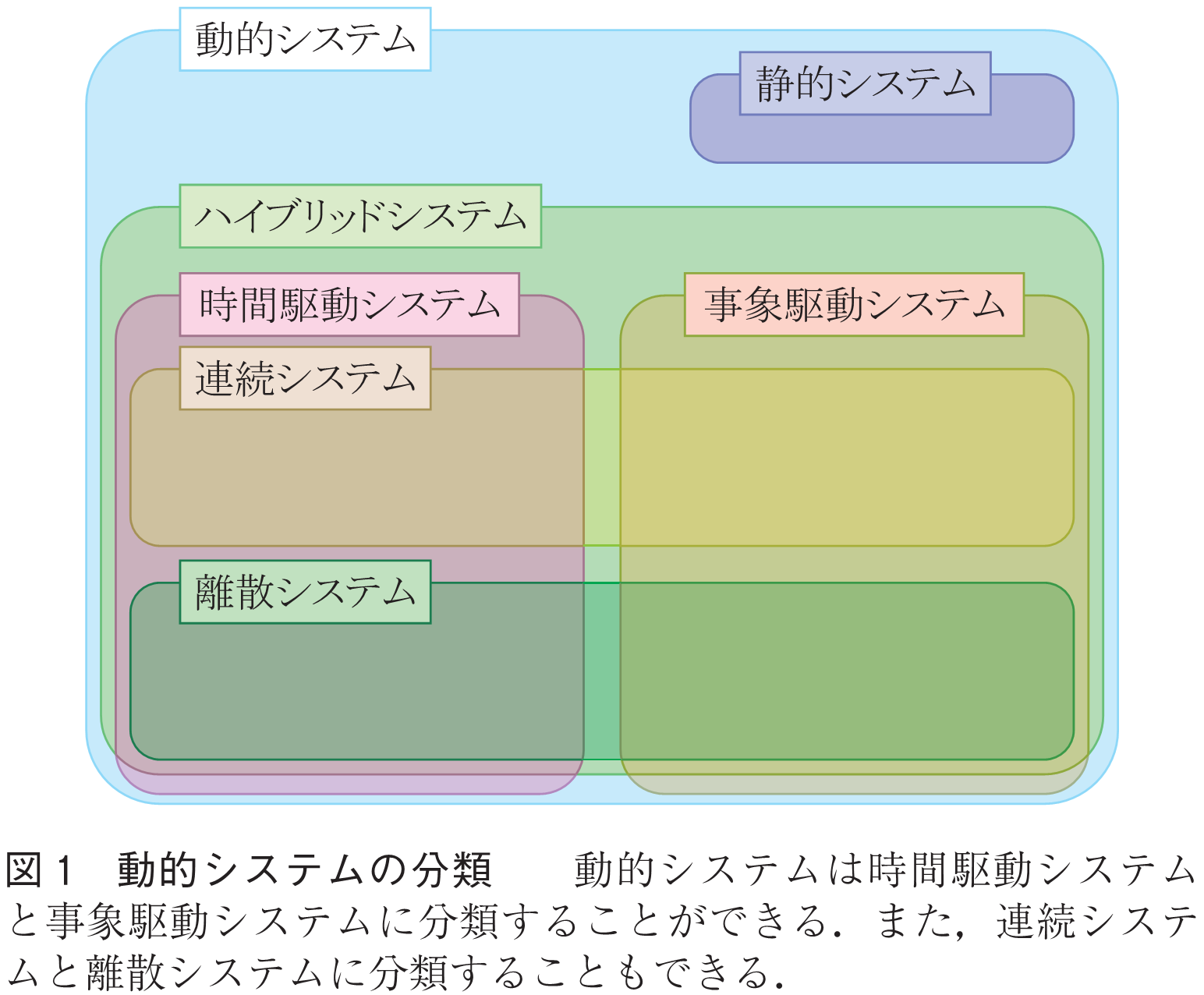
図1　動的システムの分類　　動的システムは時間駆動システムと事象駆動システムに分類することができる．また，連続システムと離散システムに分類することもできる．

　また，システムの状態が時間発展に伴い変化するシステムを時間駆動システムといい，事象の生起によって変化するシステムを事象駆動システムという．離散事象システムとは状態空間が離散集合で与えられる事象駆動システムである．離散事象システムのスーパバイザ制御に関しては本小特集3を参照されたい．

続きを読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。また、会員になると豊富な豪華特典が付いてきます。

続きを読む(PDF)　　　バックナンバーを購入する　　　　入会登録

電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。

電子情報通信学会誌会誌アプリのお知らせ

電子情報通信学会 - IEICE会誌アプリをダウンロード

小特集 1. ペトリネットの理論と応用

1．は じ め に

1．は　じ　め　に