Vol.106 No.1 (2023/1)　目次へ

CMOSインバーティブルロジック［Ⅲ・完］

――ハードウェア実現と応用例――

CMOS Invertible Logic［Ⅲ・Finish］: Hardware Implementation and Applications

鬼沢直哉

鬼沢直哉　正員　東北大学電気通信研究所

Naoya ONIZAWA, Member (Research Institute of Electrical Communication, Tohoku University, Sendai-shi, 980-8577 Japan).

電子情報通信学会誌　Vol.106 No.1 pp.58-65 2023年1月

©電子情報通信学会2023

目　　　　次

［Ⅰ］確率的双方向計算手法の基礎（10月号）

［Ⅱ］設計手法とツール（12月号）

［Ⅲ・完］ハードウェア実現と応用例（1月号）

1．は　じ　め　に

　これまで，既存ハードウェア上で双方向計算を可能にするCMOSインバーティブルロジックの概要，及び設計手法とツールについて解説してきた．最終回である今回は，確率的演算の一種であるストカスティック演算に基づくハードウェア実装方法，及びCMOSインバーティブルロジックの応用例を説明するとともに，現状の課題についても触れていきたい．

2．ストカスティック演算

　2017年に提案されたインバーティブルロジックは，確率的デバイスモデルに基づき実現されていた．その後，確率的デバイスモデルを既存のハードウェア上で近似可能な手法として，2値演算に基づく手法⁽¹⁾及びストカスティック演算に基づく手法が提案された．CMOSインバーティブルロジックはストカスティック演算に基づくハードウェア実現手法を指し，本章ではストカスティック演算について解説する．

2.1　ストカスティック演算

　ストカスティック演算は従来の2値演算のような決定論的手法とは異なり，確率的ビット列に基づき数値演算を行う手法である⁽²⁾．これまで，誤り訂正符号の一種であるLDPC（Low-Density Parity Check）符号の復号器⁽³⁾^,⁽⁴⁾，画像処理⁽⁵⁾，ディジタルフィルタ⁽⁶⁾，ハードウェアアクセラレータ⁽⁷⁾，深層学習⁽⁸⁾，脳型コンピューティング⁽⁹⁾^,⁽¹⁰⁾などに応用されてきた．

　ストカスティック演算では，数値表現にはユニポーラ符号とバイポーラ符号が存在する．ユニポーラ符号では，実数 math は確率的ビット列 math を用いて math と表現される．このとき， math はビット列 math の期待値であり，実数 math の表現範囲は0から1の間である．バイポーラ符号では，実数 math は確率的ビット列 math を用いて， math と表現され，実数 math の表現範囲は－1から1の間である．

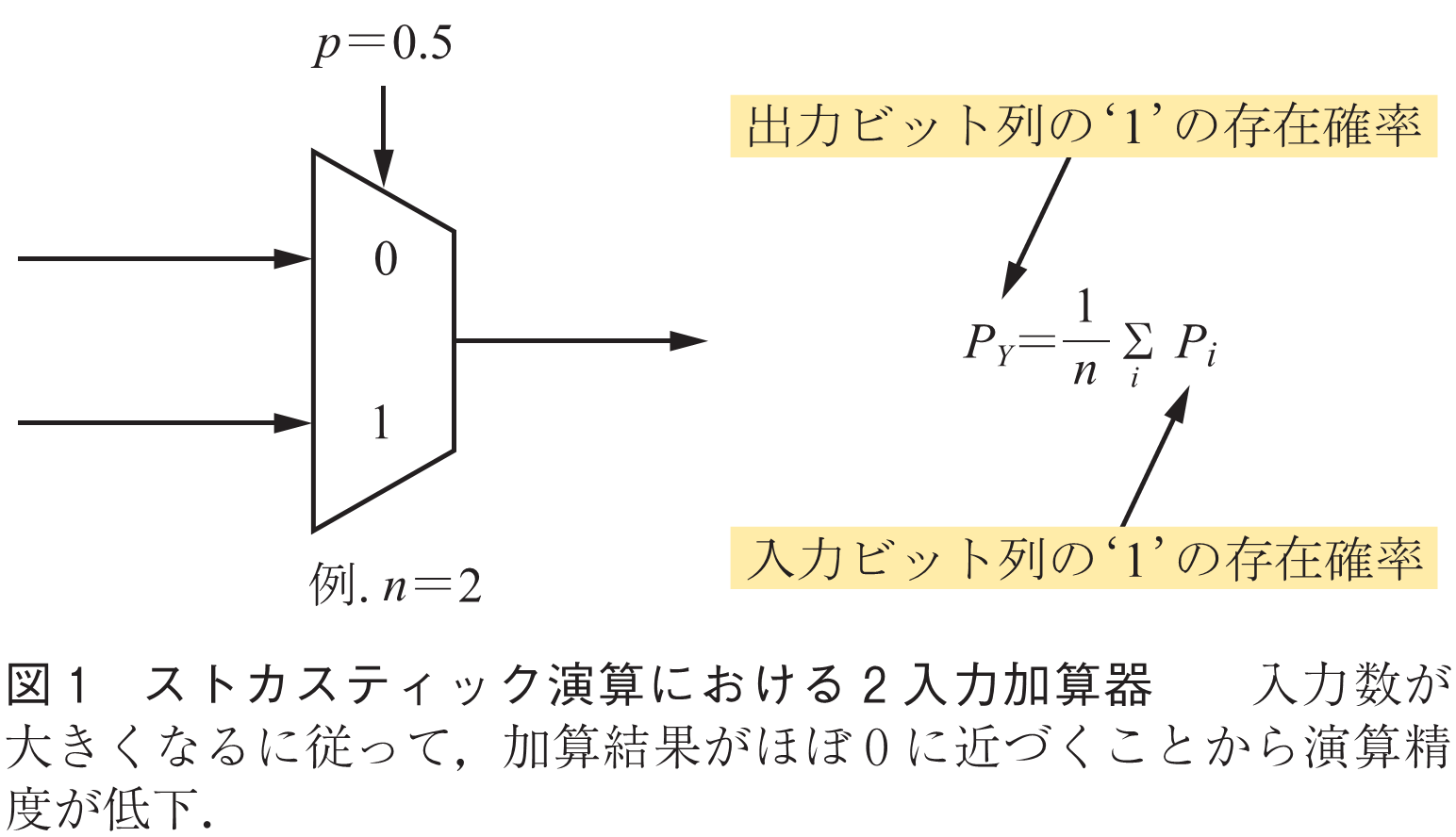
　ストカスティック演算では，乗算がANDやXNORなどのゲート一つで実現できることから，従来2値演算方式と比較してコンパクトなハードウェアが実現可能である．また，ストカスティック加算器は図1に示すマルチプレクサを用いることで実現される．2入力加算器の場合，確率的ビット列で表現された二つの信号が入力され，マルチプレクサによって二つの入力のうち，等確率でどちらか一方が出力として選択される．一方で入力数 math に応じて出力がスケーリングされるため，入力数が大きくなるに従って出力が0に近い数値となってしまうため，大きな演算誤差が課題である．

図1　ストカスティック演算における2入力加算器　　入力数が大きくなるに従って，加算結果がほぼ0に近づくことから演算精度が低下．

続きを読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。また、会員になると豊富な豪華特典が付いてきます。

続きを読む(PDF)　　　バックナンバーを購入する　　　　入会登録

電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。

電子情報通信学会誌会誌アプリのお知らせ

電子情報通信学会 - IEICE会誌アプリをダウンロード

講座 CMOSインバーティブルロジック［Ⅲ・完］――ハードウェア実現と応用例――

1．は じ め に

2．ストカスティック演算

2.1 ストカスティック演算

講座　CMOSインバーティブルロジック［Ⅲ・完］――ハードウェア実現と応用例――

1．は　じ　め　に

2.1　ストカスティック演算