
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

ジュニア会員にとって共振器やフィルタなど線形回路は比較的親しみやすい.ところが,そこへ1個でも非線形素子が入ると急に苦手意識を生じさせることがある.一つの理由は,近年の回路シミュレータ(人工知能)が高性能化し,非線形回路をゲーム感覚で解析できるようになったことが考えられる.その結果,自分の頭脳(自然知能)で回路動作を考える機会を失ってしまったのではないだろうか.本稿では,ダイオード1個とコイル・コンデンサ(LC素子)からなる極めてシンプルな回路を例に挙げ,その電圧電流の振舞いを自然知能で解明することに挑戦する.
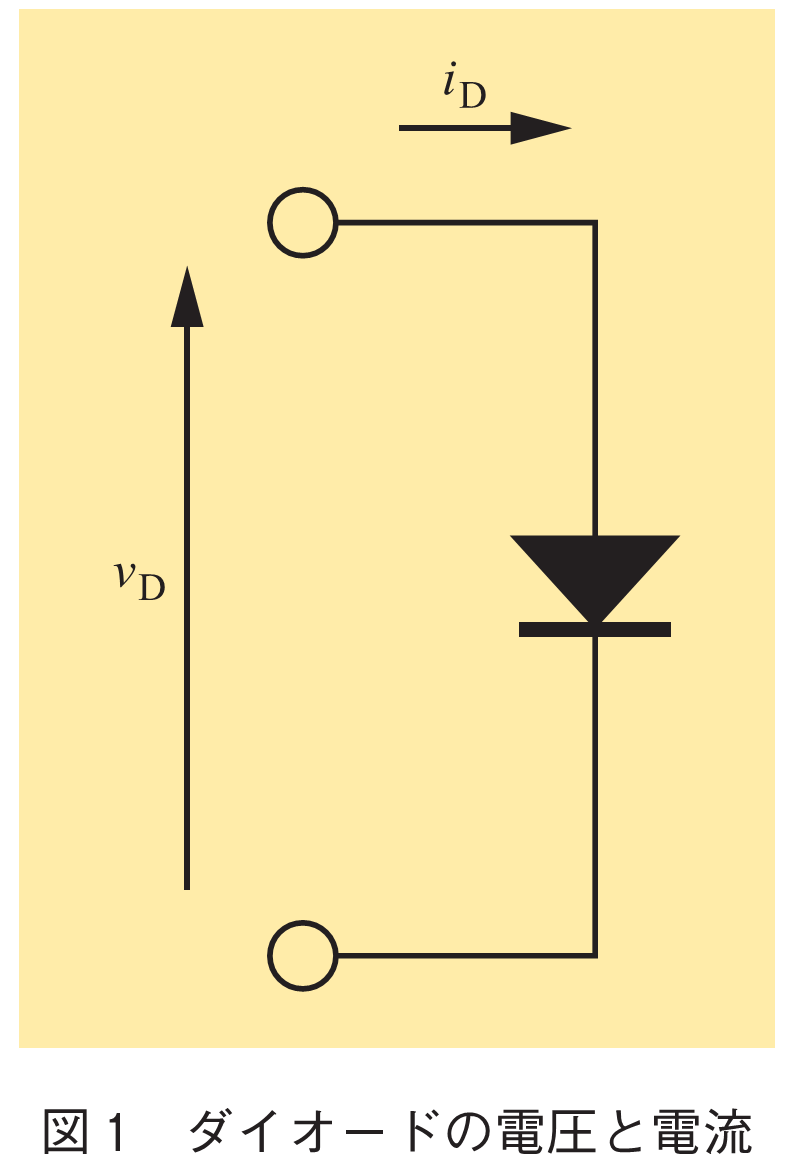
物理の授業でダイオードは「一方向にだけ電流が流れる」と教わる.親しみやすく自動車道の一方通行ゲートに比喩して説明される.ダイオードの電圧と電流
を図1のように定義しよう.この場合,電流が下向きにだけ流れる.これを順方向と呼ぶ.数式で書くと
である.ダイオードに電流が流れている状態をオン状態と呼ぶ.このときダイオード内の電圧降下が完全にゼロとなっているのが理想である.これを
と書く.以上をまとめて
(1)
と書く.
ダイオードに逆方向の電圧をかけると電流が流れない.この状態をオフ状態と呼ぶ.このときダイオード内の漏れ電流が完全にゼロとなっているのが理想である.これを
(2)
と書く.これら二つの状態を接続する点として電圧・電流共にゼロとなることがある.これを
(3)
と書く.本稿で登場するダイオードは上記3状態のどれかを採るものとする.これを理想ダイオードと呼ぶ.
式(1)と式(2)を並べてみると,これはと
について対称性の良い関係となっていることが分かる.したがって,ダイオードが「一方向にだけ電流が流れる」と習うなら,併せて「電圧も一方向にだけかかる」と悟ることができる.つまり,電圧と電流を平等に扱うことがポイントである.
ダイオードにコイルを直列接続した回路を図2に示す.直列接続なので回路全体を流れる電流はコイルとダイオードで共通
(4)
である.電圧はコイルとダイオードに分圧されて
(5)
となる.電流の時間変化に比例する電圧
(6)
がコイルに誘起される.この比例定数をコイルのインダクタンスと呼ぶ.
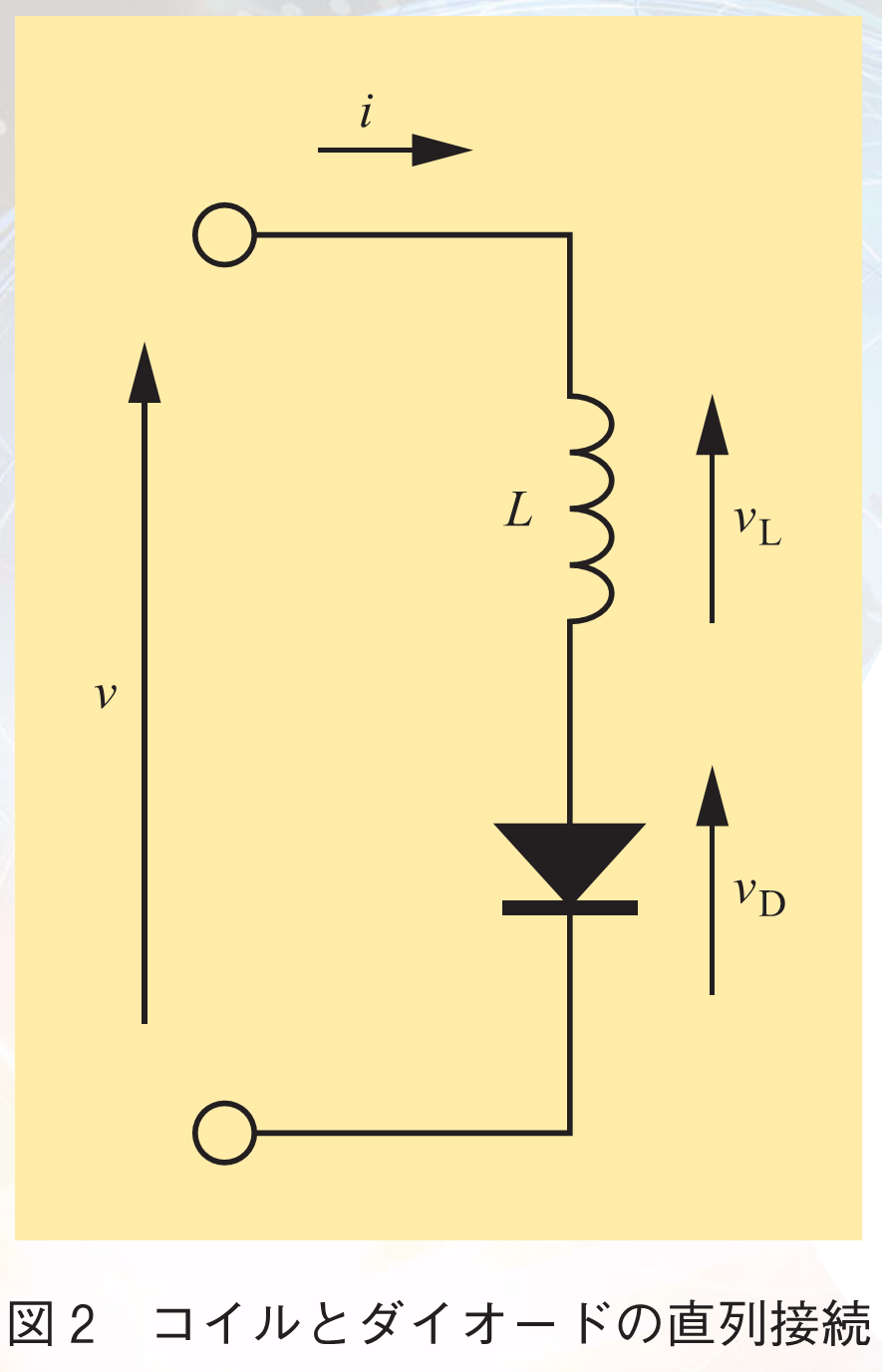
この回路に入力電圧を与えたときのダイオード電圧
を求める問題を考えよう.もし
が直流電圧の場合はコイル
が単なるリード線とみなせる.よって答えは自明,
である.問題として意味が出てくるのは
が時間とともに変化する場合である.4.でそれを考える.
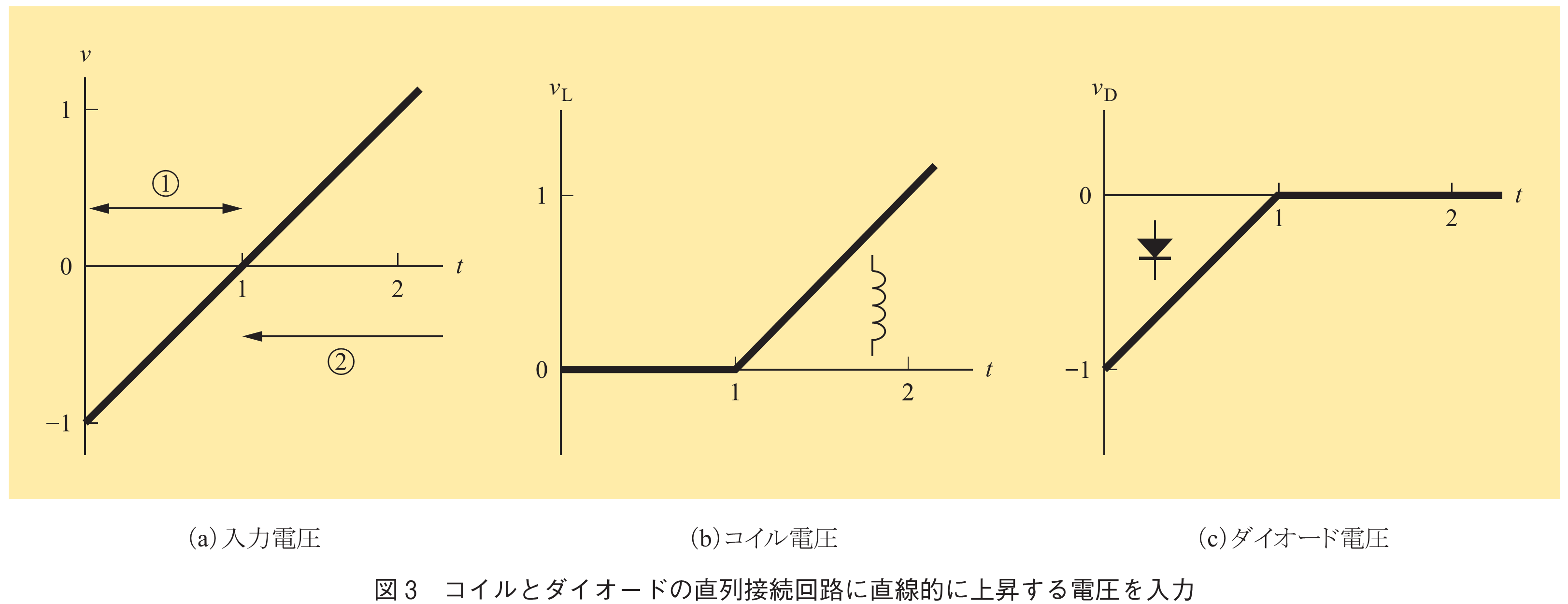
時間変化する入力電圧の例を図3のグラフ(a)に示す.時刻
で負の電圧からスタートし,そこから直線的に上昇させる.簡単のため電流の初期値は
とする.これに伴って,ダイオード電圧
はどのように変化するだろうか.各区間ごとに考えるのが分かりやすい.
まず最初の区間①を考えよう.で
である.この直後に電流はどうなるだろうか.電流の初期値は
である.そこから仮に電流が流れ始めるとしても最初の時間傾斜はダイオードの逆方向にはなり得ない.そうすると式(6)から
である.この区間は
なので式(5)から
となる.ダイオードがとり得る3状態のうちこの不等式を満たすのは式(2)すなわちオフ状態だけである.よって式(4)から
である.電流値が初期から変わっていない.この論理は区間①内で帰納法的に繰り返すことができる.つまり
である限りオフ状態が続くのである.結論:区間①全体で
が維持される.
時刻で
が0まで上がる.それに連動して
も0まで上がる.電流は依然として流れていない.この瞬間が式(3)で述べたダイオードの中立状態である.
それ以降の区間②では電圧・電流が区間①と真逆の振る舞いをする.ダイオード電圧は3状態どれであっても正にはなり得ない.つまりである.この区間は
なので式(5)から
となる.よって式(6)から電流の時間傾斜は正である.結論:区間②では
すなわちダイオードのオン状態が続く.
以上の結果を図3のグラフ(b),(c)にまとめる.時刻でダイオードがオフ状態からオン状態に変わる.これをターンオン動作と呼ぶ.入力電圧
が滑らかな直線であるにもかかわらず
と
が共に折れ線となる.それまでダイオードにかかっていた電圧が
の瞬間にコイル側へ乗り移る.あるいは引き継がれるという言い方もできる.これが直列コイル装荷ダイオードのターンオン動作の特徴である.
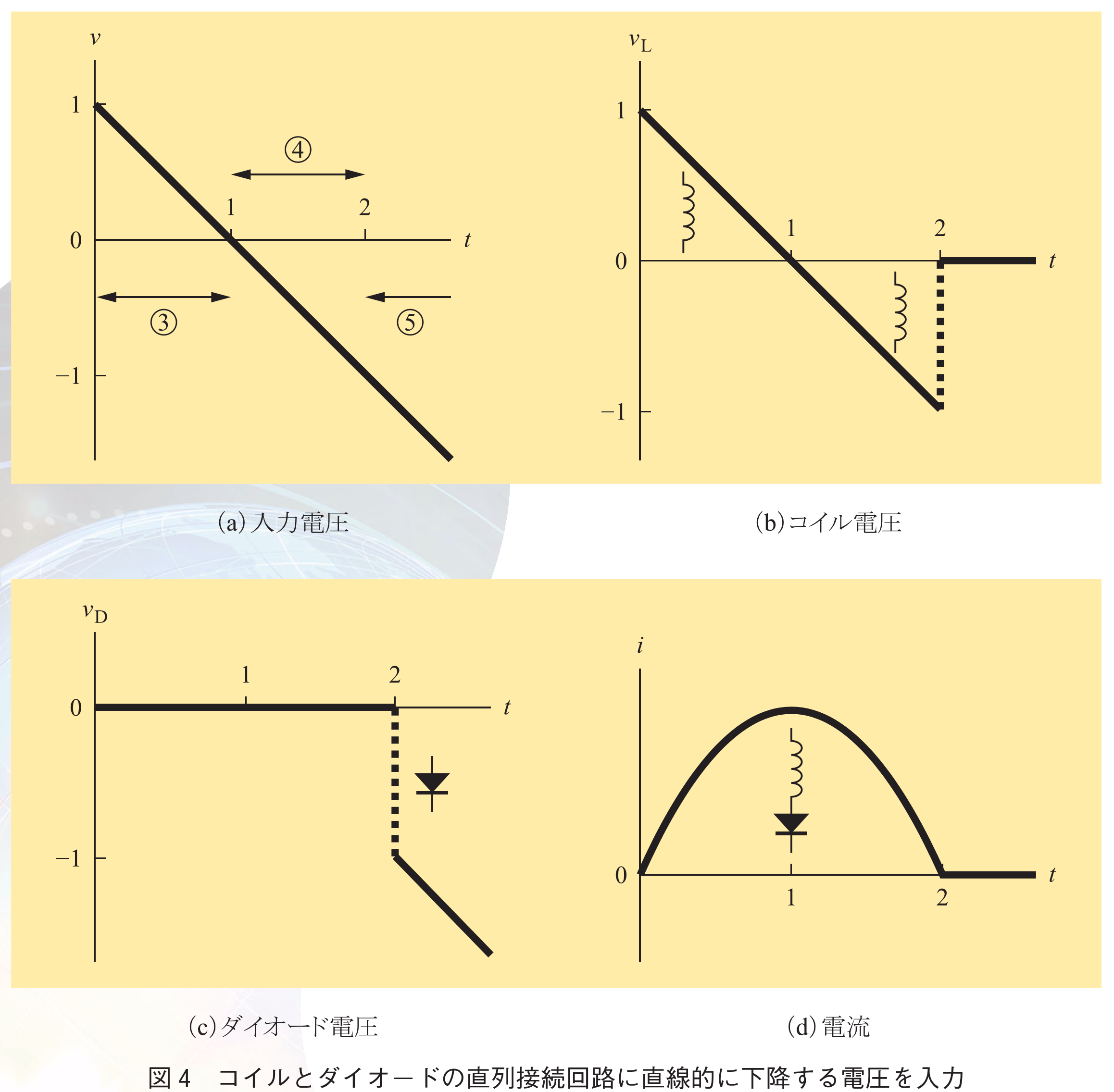
図2の回路において入力電圧が直線的に下降する場合はどうなるだろうか.入力電圧の時間変化を図4のグラフ(a)に示す.4.同様,時間軸上の区間に分けて考えよう.
最初の区間③ではダイオードがオン状態つまりとなる.その理由は4.の区間②と同じである.電圧が徐々に降下し続け,
で
となる.そうすると4.の
と同様にここで中立状態となるのでは・・と思いきや,それは早合点.実はこの瞬間まだ電流
がしっかり流れているのだ.なぜこんなことが起こるのだろうか.それはオン状態で流れている電流
がコイルにも共通で流れているため,コイルに磁束エネルギーが蓄積されており,これを急に0にすることができないからである.
この状況が区間④まで続く.電圧で言うとが負になった分を
が補って
となっている.そして,コイルが磁束エネルギーを完全放出するのは時刻
である.これでようやく電流も0に戻る.その瞬間にダイオードがオフ状態に移る.これがこの回路におけるターンオフ動作である.その後の区間⑤では4.の区間①と同じ状況となる.この区間
なので入力電圧がコイルで電圧降下することなくフルにダイオードに届く.これによりダイオードのオフ状態が維持される.
以上の結果を図4のグラフ(b)(c)(d)にまとめる.これらグラフが各区間で式(5),(6)を満たしていることを目視で認識できれば理解が定着する.加えて注目すべきはグラフ(b)と(c)にある2本の破線である.時刻で
と
が共にジャンプする.これは4.のターンオン動作では見られなかった現象である.コイルとダイオード間で電圧が乗り移る(引き継がれる)という意味では同じであるが,その際に電圧ジャンプすなわち不連続な遷移を伴うという点が明らかに異なる.これが直列コイル装荷ダイオードのターンオフ動作の特徴である.
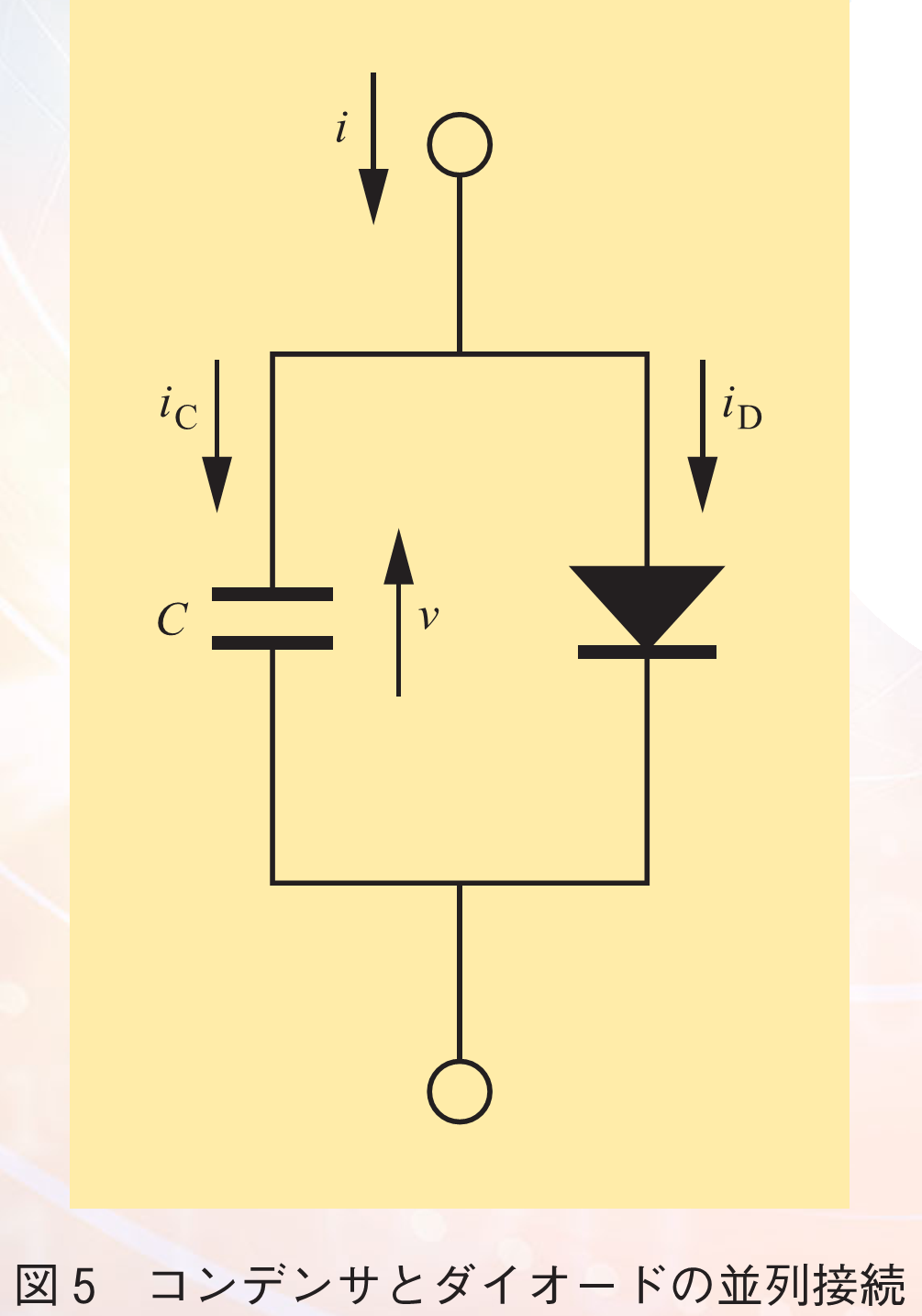
ダイオードを用いるシンプルな回路例をもう一つ紹介する.図5に示すようにダイオードに並列コンデンサを付加する.並列接続なのでコンデンサとダイオードで電圧が共通
(7)
である.電流はコイルとダイオードに分流されて
(8)
となる.電圧の時間変化に比例する電流
(9)
がコンデンサに流れ込む.この比例定数をコンデンサの容量と呼ぶ.
この回路に入力電流を与えたときのダイオード電流
を求める問題を考えよう.もし
が直流の場合はコンデンサ
が単なる端子台とみなせる.よって答えは自明,
である.問題として意味が出てくるのは
が時間とともに変化する場合である.
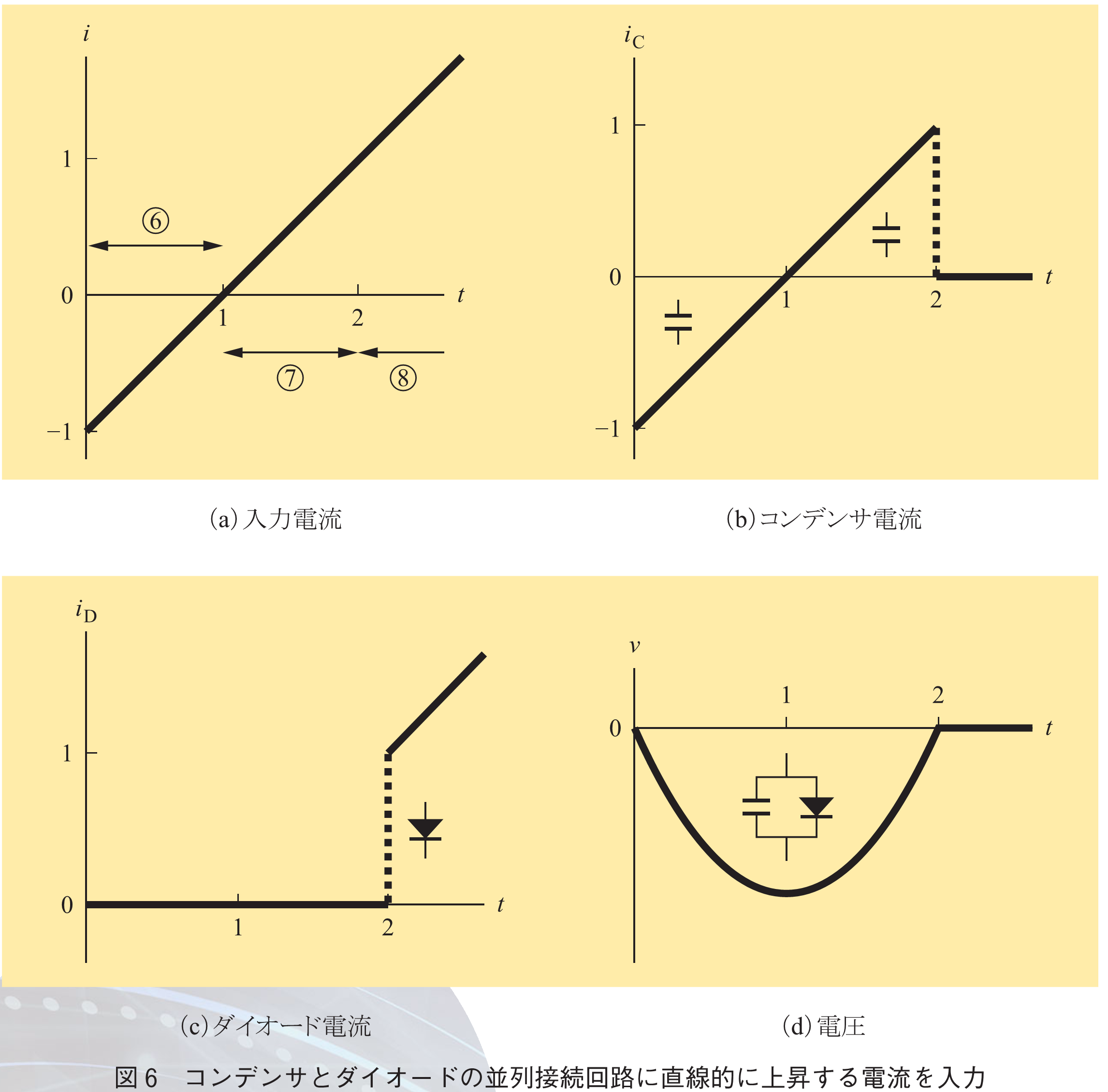
時間変化する入力電流の例を図6のグラフ(a)に示す.時刻
で負の電流からスタートし,そこから直線的に上昇させる.簡単のため電圧の初期値は
とする.これに伴って,ダイオード電流
はどのように変化するだろうか.5.同様,各区間ごとに考えるのが分かりやすい.
最初の区間⑥では負の電流が入力されるのでダイオードがオフ状態つまりとなる.電流が徐々に上昇し続け,
で
となる.入力電流が0でもこの瞬間まだ電圧
はしっかり残っている.それはオフ状態でダイオードにかかっているがコンデンサにも共通でかかっているため,コンデンサに電束エネルギーが蓄積されており,これを急に0にすることができないからである.
この状況が区間⑦まで続く.電流で言うとが正になった分を
が補って
となっている.そして,コンデンサが電束エネルギーを完全放出するのは時刻
である.これでようやく電圧も0に戻る.その瞬間にダイオードがオン状態に移る.これがこの回路におけるターンオン動作である.その後の区間⑧では
なので入力電流がコンデンサに分流されることなくフルにダイオードに届く.これによりダイオードのオン状態が維持される.
以上の結果を図6のグラフ(b)~(d)にまとめる.これらグラフが各区間で式(8),(9)を満たしていることを目視で認識できれば理解が定着する.加えて注目すべきはグラフ(b)と(c)にある2本の破線である.時刻で
と
が共にジャンプする.これは5.の回路のターンオフ動作と同様の現象である.コンデンサとダイオード間で電流が乗り移る(引き継がれる).その際に電流ジャンプすなわち不連続な遷移を伴う.これが並列コンデンサ装荷ダイオードのターンオン動作の特徴である.
ここまでの説明を見て洞察力ある読者は何かに気づいたのではないだろうか.6.の議論は5.と非常に類似している.具体的に言うと
○電圧 電流
○磁束 電束
○直列 並列
○オン オフ
○コイル コンデンサ
という相互交換をすることで同じ説明文になる.このような対応関係がある二つの物理現象を「互いに双対である」と言う.グラフ的に見ても図4と図6が双対の関係となっていることが分かる.これらのグラフで最も特徴的な共通点は時刻におけるジャンプ現象である.
ダイオード1個とLC素子から成るシンプルな回路を自然知能で探訪した.回路構成が極めて単純なので加減算と初歩的微積分だけで脳内シミュレーションできる.このとき理想ダイオードの3状態をきちんと認識することが正しい理解への要点である.結果のグラフから,入力の時間変化が連続的であっても回路内部で不連続すなわちジャンプ現象が生じるのだという気づきを得た.電圧・電流のジャンプは高周波パワエレの重要な基本真理の一つである.この真理をしっかり身につけることでE級整流(1)~(3),(用語)など高性能ダイオード回路へのチャレンジが可能となる.
(1) 大平 孝,“E級整流の美しき動作理論,”トランジスタ技術パワエレ特集号,vol.59, no.8, pp.206-208, Aug. 2022.
(2) T. Ohira, “Linear algebra elucidates class-E diode rectifiers,” IEEE Microw. Mag., vol.23, no.12, pp.113-122, Dec. 2022.
(3) T. Ohira, “Inductor and diode,” IEEE Microw. Mag., vol.24, no.1, Jan. 2023.
(2022年7月23日受付 2022年8月5日最終受付)
■ 用 語 解 説
オープンアクセス以外の記事を読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード