
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

マルチメディア情報ハイディング・エンリッチメント研究専門委員会
秘密分散法を用いた秘匿演算
秘匿演算(秘密計算とも呼ばれる)とは,データを暗号化したままの状態で様々な演算ができる技術のことである.
例えば,Aは自分の年収が,周りの人の平均より高いのか低いのかを知りたい場合を考える.年収は個人情報の一つであるため,周りの人の年収をそのままAに渡すと,個人情報が漏えいする可能性がある.そこで,年収を含む個人情報の機密性を満たすために,データを暗号化して渡す必要がある.しかし,従来の情報処理技術では,暗号化した情報の処理ができないため,データの演算処理の過程で,暗号化したデータを一時的に復号して演算する必要がある.しかし,復号した情報により,個人情報が漏えいする可能性がある.
それに対して,秘匿演算を利用することにより,信頼できない環境においても,暗号化した情報を復号することなく演算することができ,生データと同じ精度で分析を行うことができるため,データの漏えいや不正利用のリスクを回避できる.すなわち,Aは,秘匿演算を利用すれば個々の人の年収を知らなくても,その結果を知ることができる.
秘匿演算を実現するために,幾つかの手法があるが,近年では,大きく以下の二つが注目されている.
(1)準同形暗号
(2)秘密分散
準同形暗号では,鍵を用いて情報を暗号化し,加算と乗算両方の演算を暗号化したまま実現できる暗号方式であり,1台の計算機(以降,サーバとする)で演算の処理を実現でき,シンプルで構築しやすいという利点があるが,一般的に計算量が多く,演算の処理に多大な時間がかかり,超高速で高性能なサーバが必要になるという問題がある.
秘密分散とは,ある情報を複数の異なる値(以降,分散値と呼ぶ)に変換し,複数のサーバに保管する手法である.準同形暗号に比べて,演算速度が格段的に速いという利点があるが,高速な通信網でつながれている複数台の高性能なサーバ上で処理をする必要があり,サーバ間の通信も多いという問題がある.
ただし,膨大なデータを扱うビッグデータの解析や人工知能による機械学習への適用を考えた場合,計算が軽く高速処理が可能な秘密分散が適していると考えられる.
秘密分散は文献(1)に記述があるが,加法的秘密分散や(,
)しきい値秘密分散など(ISO/IEC 19592-2 : 2017 Secret Sharing)がある.
また,近年では,分散システム,特に秘密分散を用いた秘匿演算(MPC : Multi-Party Computationとも呼ばれる)を実行するのに一般的に使われている仕組みとしては,クライアントサーバモデルが注目される.クライアントサーバモデルは,図1に示すように,秘密情報を与えるクライアント(入力者),秘匿演算を行う複数台のサーバと秘匿演算結果を復元するクライアント(復元者)から構成される.
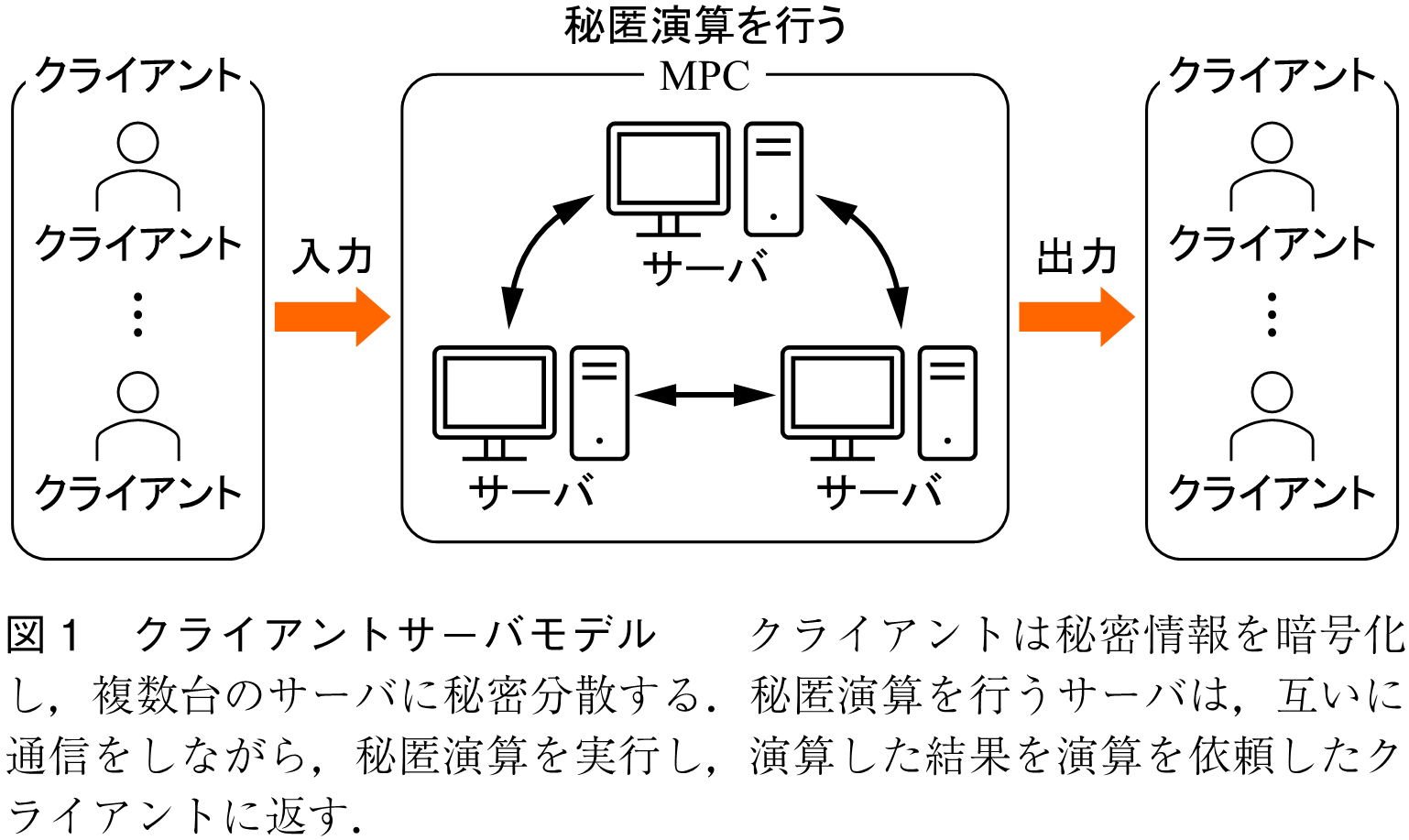
次に,先ほどの課題である「年収を秘匿しながら周りの人の平均年収を求める」場合を例として,以下に秘密分散を用いた秘匿演算の仕組みを簡単に解説する.
例えば,表1にAとその周りの人物B,Cの年収を示す.ここでは,簡単のために,秘密分散の一つである加法的秘密分散を考える.Aは,自分の年収を秘密分散する際に,(Aの年収=+
+
)の関係が成り立つ三つの乱数
,
,
を選び,それぞれをサーバ1,2,3に送信する.
例えば,Aは=272,
=41をランダムで選び,
=Aの年収-
-
=127を計算し,サーバ1,2,3に送信する.B,Cも同様な処理を行い,サーバに秘密分散する.
これによって,各サーバはA,B,Cの年収の分散値を保持するが,これらの分散値が全てそろわなければ,元の年収は漏えいしないという特徴を実現できる.
次に,各サーバが持つ分散値を用いて,秘匿演算で平均年収を求める方法について解説する.表1から,(272,40,195)はサーバ1が持つユーザA,B,Cの年収の分散値である.サーバ1はこれらの分散値を用いて,その平均値=169を計算し,Aに送信する.サーバ2,3も同様な処理を行い,計算した平均値をAに渡す.
最後に,Aは送られてきた分散された平均値(169,158,173)を足して,3人の平均年収=500を求めることができる.これによって,Aは,BとCの年収を知らなくても,その演算結果である平均年収を知ることができる.
3.で説明した加法的秘密分散((,
)しきい値秘密分散とも呼ばれる)では,生成した分散値のうち,1個でも欠損したら,元の情報を復元できなくなる.対して,(
,
)しきい値秘密分散では,
個の分散値のうち,任意の
個以上集めれば,元の秘密情報を復元できるため,
台のサーバ欠損耐性を持つ.しかし,代表的な(
,
)しきい値秘密分散法であるShamirの(
,
)しきい値秘密分散(2)を用いても次のような問題点が発生する.
Shamirの(,
)しきい値秘密分散は多項式を用いて秘密分散を行う.よって,乗算する
,
を
,
で分散し,各サーバが保持している分散値をそのまま乗算すると,乗算した結果の分散値
=
の次数は,図2に示すように,
から
に増加してしまう.そのため,分散式
を復元するには,
個の分散値を保存するサーバが必要になる.また,演算を繰り返せるように
次の分散値を
次の分散値に戻すにはサーバ間の通信を必要とし,その通信時間が処理速度に影響する場合が多い.

よって,秘密分散を用いた秘匿演算を効率的に行うには,乗算による次数変化と複数サーバ間の通信による処理速度への影響にどう対応するかがポイントになる.5.に代表的な秘密分散を用いた秘匿演算を紹介する.
Ben-Orらは,1988年に,生成した多項式の次数を減らす方法を導入した(3).各サーバは分散値同士で乗算した結果を次多項式で全サーバに再分散を行う.また,再分散された分散値をラグランジュ係数と定数倍乗算し,分散値を加算することで,
次式の多項式を得る.ただし,
.
Damgardらは,2012年に,BeaverのMultiplication Triple(の関係を満たす乱数
,
,
の分散値)をSHE(Somewhat Homomorphic Encryption)で事前に生成し,
=
(最小2台のサーバ)の設定でも実現できる秘匿演算を提案した(4).ただし,SHEによる事前処理の計算コストが膨大になり,サーバ間の通信も発生する.
Arakiらは,2016年に,(,
)しきい値秘密分散における
,
を固定し,1回の通信で乗算を実現できる秘匿演算を提案した(5).Arakiらの秘匿演算法では,3台のサーバそれぞれ,
の関係を満たす乱数
,
,
(Correlated Randomnessと呼ぶ)を持つという前提で,乗算を実現する.ただし,この乱数組の生成によって,全体の計算量が増える可能性がある.
5.2,5.3で述べたように,補助情報を事前に計算しても計算量が大きいという問題が残る.近年では,TTP(Trusted Third Party),TEE(Trusted Execution Environment)や不正を行う誘因のないユーザなど,信頼できるエンティティを想定する方法が注目されている.例えば,岩村らの秘匿演算(TUS方式)では,攻撃者が知らない乱数の生成処理をTTPが行うことで,低通信量・計算量の秘匿演算を実現できる(6).
(1) 岩本 貢,“13-3 秘密分散,”信学知識ベース“知識の森,”1群1編13章,電子情報通信学会,2019.
(2) A. Shamir, “How to share a secret,” Commun. ACM, vol.11, no.22, pp.612-613, Nov. 1979.
(3) M. Ben-Or, S. Goldwasser, and A. Wigderson, “Completeness theorems for non-cryptographic fault-tolerant distributed computation,” Proc. STOC 1988, pp.1-10, ACM, 1988.
(4) I. Damgård, V. Pastro, N. Smart, and S. Zakarias, “Multiparty computation from somewhat homomorphic encryption,” Proc. CRYPTO 2012, pp.643-662, 2012.
(5) T. Araki, J. Furukawa, Y. Lindell, A. Nof, and K. Ohara. “High throughput semi-honest secure three-party computation with an honest majority,” Proc. CCS 2016, pp.805-817, 2016.
(6) K. Iwamura and A.A.A.M. Kamal, “TTP-aided secure computation using (k, n) threshold secret sharing with a single computing server,” IEEE Access, vol.10, pp.120503-120513, 2022.
(2022年12月18日受付)
オープンアクセス以外の記事を読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード