Vol.107 No.11 (2024/11)　目次へ

知識の森

応用音響研究専門委員会

音源分離

伊藤信貴（東京大学）坂東宜昭（産業技術総合研究所）

本会ハンドブック「知識の森」

https://www.ieice-hbkb.org/portal/doc_index.html

1．音源分離とは

　音源分離⁽¹⁾^～⁽³⁾とは，マイクロホンで録音された混合音を個々の音源からの信号（以下，「音源信号」）に分離する技術であり，多くの応用がある．例えば，会話中に複数の話者の発話が重なると，音声認識の性能が極端に低下することがある．このような場合でも，音源分離により話者ごとに音声を分離すれば，正確な音声認識を実現可能である．また，楽曲の録音を各楽器の音に分離することもできる．更に，音声や楽音に限らず，一般の環境音を異なる種類の音（鳥の鳴き声，車の通過音など）に分離することも可能である．

2．音源分離のアプローチ

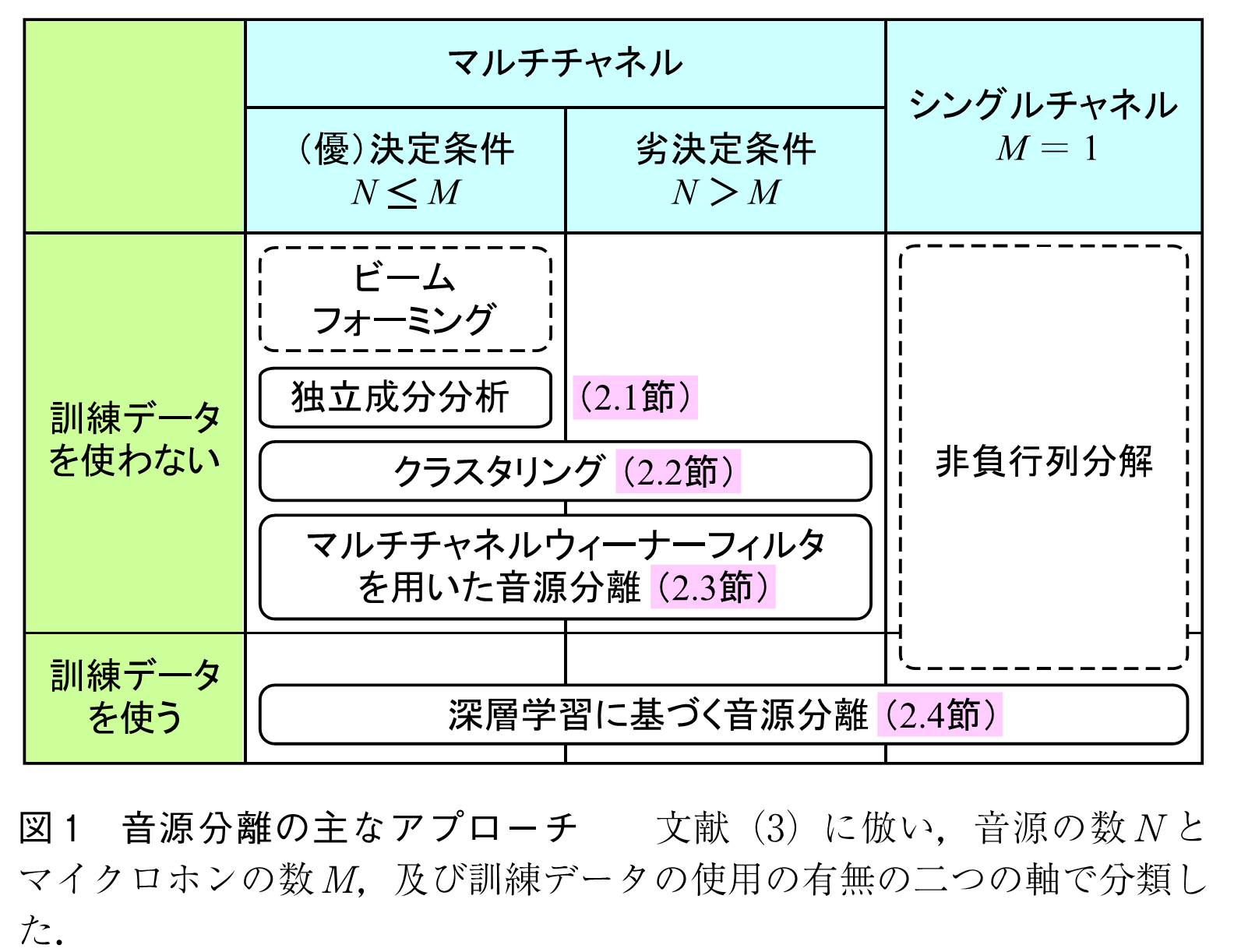
　本稿では，図1に示す音源分離の主なアプローチのうち，実線で囲まれた四つについて説明する．誌面の都合上，破線で囲まれた二つについては文献（１），（２）に譲り，ここでは割愛する．

図1　音源分離の主なアプローチ　　文献（３）に倣い，音源の数Nとマイクロホンの数M，及び訓練データの使用の有無の二つの軸で分類した．

2.1　独立成分分析に基づく音源分離

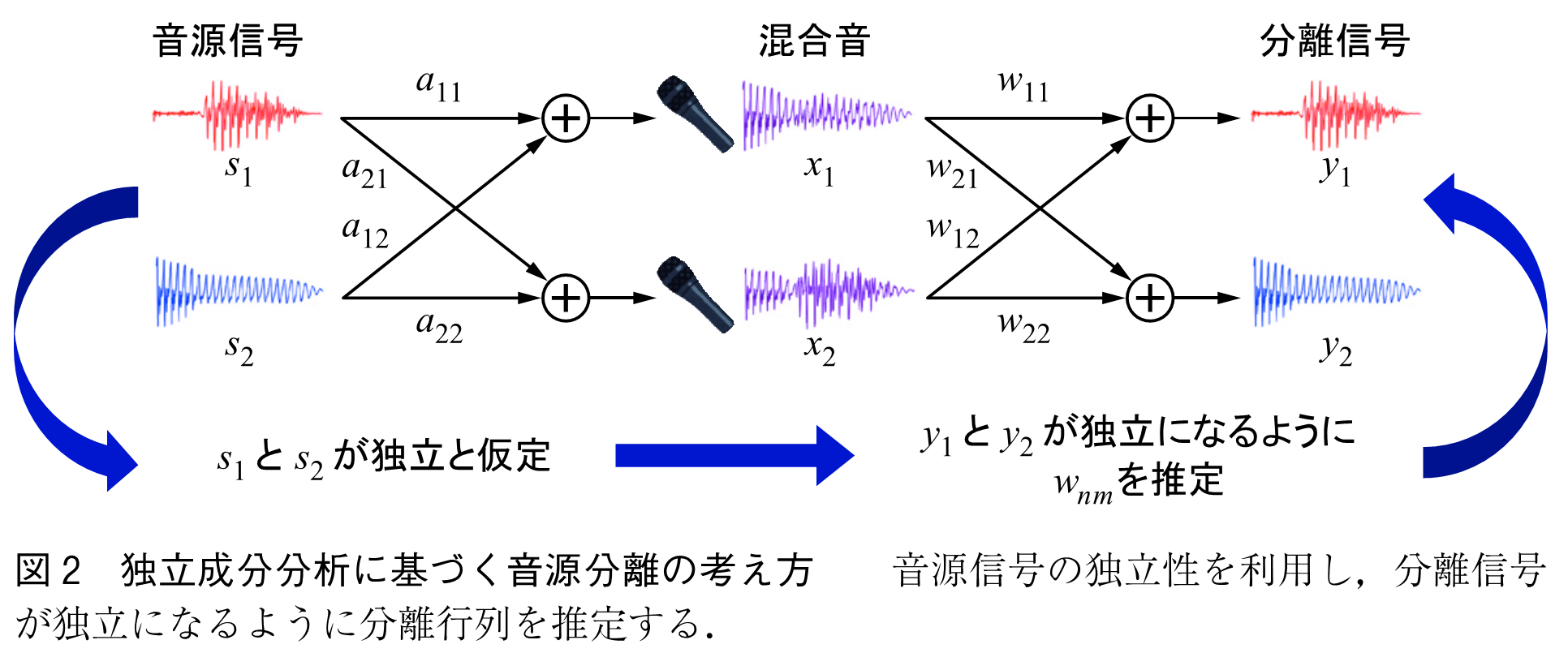
　独立成分分析⁽⁴⁾に基づく音源分離⁽¹⁾^～⁽³⁾は，音源の数 math がマイクロホンの数 math 以下である（優）決定条件 math を対象とし，音源信号の統計的独立性を利用する（図2）．これは，音源信号の到来方向の事前知識や訓練データを必要としないブラインド音源分離技術の一つである．以下では簡単のため， math の場合について説明する．

図2　独立成分分析に基づく音源分離の考え方　　音源信号の独立性を利用し，分離信号が独立になるように分離行列を推定する．

　観測された混合音は，次の線形モデルで表される．

math

（１）

ただし， math は math 個のマイクロホンで観測された混合音の短時間フーリエ変換からなるベクトル（ math と math は時間と周波数の番号）， math は math 個の音源信号の短時間フーリエ変換からなるベクトル， math は混合行列である．

　本アプローチにおける基本的な考え方は次のとおりである．式（１）において逆行列 math が存在すれば，分離行列 math が存在し，分離信号 math が次式で与えられる．

math

（２）

math は， math の各要素が独立になるように推定する．例えば，相互情報量や非ガウス性，ゆう度を用いた勾配法，自然勾配法，補助関数法などのアルゴリズムが提案されている．

　本アプローチに基づく多くの手法では，周波数ごとに個別に math を推定し， math の要素の順序とスケールが定まらないという問題がある．この問題については，後処理で解決する方法や，全ての周波数成分を連結した多変量モデルまたは音源信号の非負行列分解モデルを用いて回避する方法が提案されている⁽¹⁾^,⁽³⁾．

2.2　クラスタリングに基づく音源分離

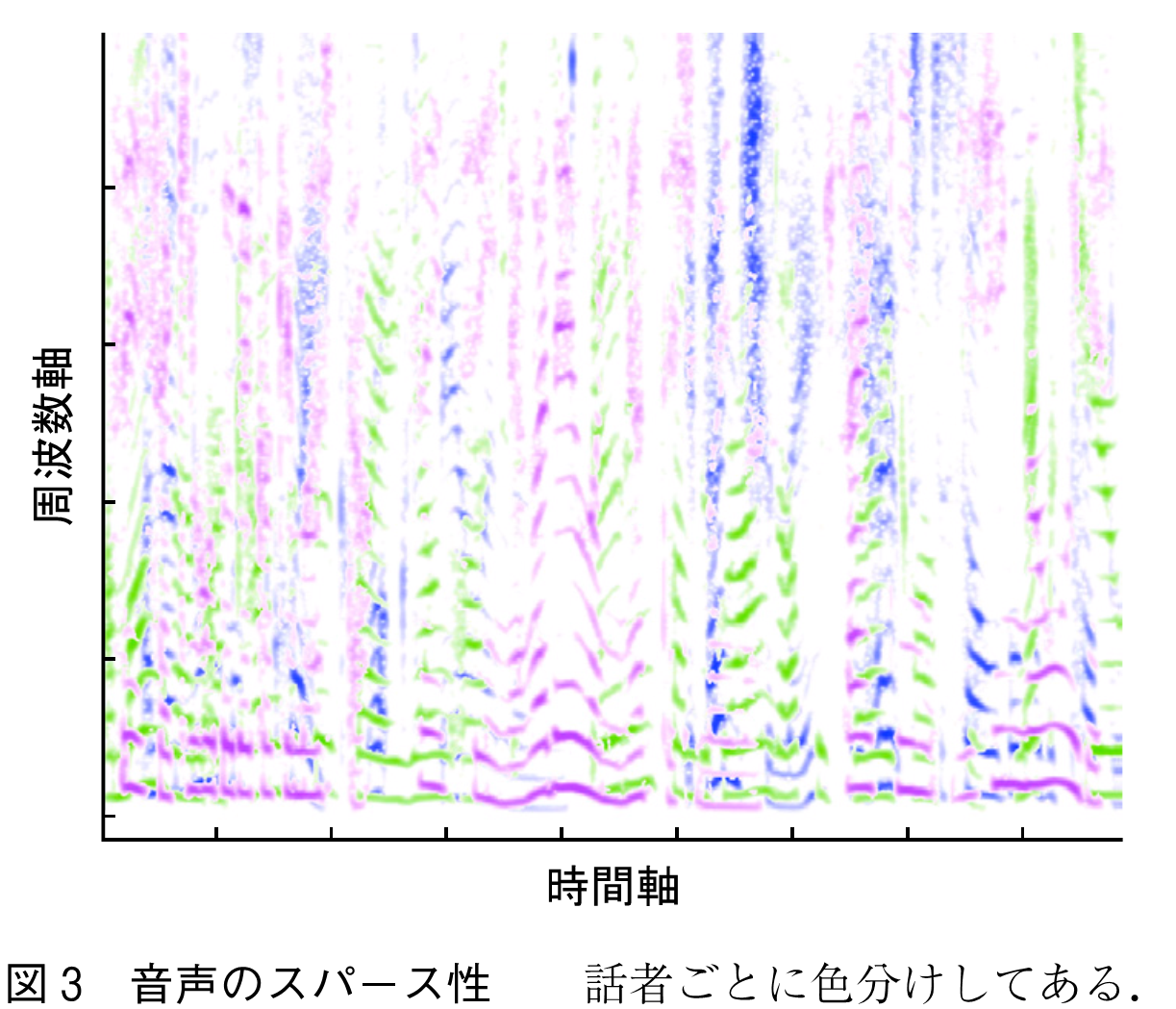
　クラスタリングに基づく音源分離⁽¹⁾^,⁽⁵⁾は，音声を対象とし，音声のスパース性を利用することにより，劣決定条件下でもブラインド音源分離を可能にする．スパース性とは，少数の成分のみが大きい値をとり，他の成分はほぼ0であるという性質である．この技術により，例えばICレコーダの二つのマイクロホンで三人の話者の重なった音声を分離可能である．

　図3のように音声の短時間フーリエ変換はスパースであり，複数の話者が同時に話しても，時間周波数成分が余り重ならない．そこで，混合音声の各時間周波数成分はただ一人の話者に由来する（排反性）とモデル化する⁽⁵⁾．そして，各話者に対応する時間周波数成分を抽出することにより音源分離を実現する．具体的には，マイクロホン間の到来時間差などの音の到来方向に関する特徴量を用いて， math -means法や混合ガウス分布により混合音声の時間周波数成分を話者ごとにクラスタリングできる．特に，混合複素角度中心ガウス分布を用いた方法⁽⁶⁾により，高い分離性能が得られる．

図3　音声のスパース性　　話者ごとに色分けしてある．

　しかしながら，楽曲の録音を楽器ごとに分離する場合など，上述の排反性が成り立たない場合も多く，そのような場合には本アプローチは適さない．

2.3　マルチチャネルウィーナーフィルタを用いた音源分離

　一方，マルチチャネルウィーナーフィルタを用いたアプローチ⁽¹⁾では，排反性を仮定せずに劣決定条件下でのブラインド音源分離が可能である．この技術により，例えば楽曲のステレオ録音を三つの楽器音に分離できる．

　マルチチャネルウィーナーフィルタとは，平均二乗誤差を最小化する最適な線形フィルタである．我々の目標は，混合音 math が与えられたときに，各音源に由来する成分 math を推定することである．線形推定器

math

（３）

で平均二乗誤差を最小化するものは

math

（４）

で与えられる．ここで， math は math の共分散行列^(注1)，上付きのHはエルミート転置，Eは期待値である．式（４）をマルチチャネルウィーナーフィルタと呼び，これが得られれば式（３）により音源分離を実現できる．

　式（４）を計算するには math が必要であるが，この音源ごとの行列を観測された混合音から，いかに正確に推定するかが鍵となる．これに対し，音源信号の確率モデルに基づいて，観測された混合音が生成される確率（ゆう度）を最大化することにより， math を推定する手法が提案されている．そのような手法の多くは膨大な計算量を要するという難点があったが，近年，同時対角化を用いることで計算量を大幅に削減する方法が提案され，現実的な計算量での処理が可能になった⁽⁷⁾．

2.4　深層学習に基づく音源分離

　このアプローチでは，事前に収集した訓練データを用いて深層学習モデルのパラメータを最適化し，訓練データと似た未知データに対する音源信号の予測に使用する．多くの枠組みでは，混合音と音源信号のペアデータを準備し，その間の写像を回帰する教師あり学習が行われる．例えば，楽音分離であれば楽曲の録音と各楽器の個別トラックを，音声分離であれば会話の録音と個々の音声信号を準備する．表現力の高いモデルを用いることで圧倒的な性能を発揮できるが，十分汎化できるほどの膨大な音源信号を準備するには高いコストを要する．

　音源信号の準備コストを回避するため，混合音のみを訓練データとして用いる教師なし学習も開拓されている．シングルチャネル音源分離では，ランダムに選択した混合音を更に混合した混合混合音を用いる混合不変学習⁽⁸⁾が代表的である．この枠組みでは，分離結果を足し合わせた結果がそれぞれの混合音を再構成するように学習する．また，2.1から2.3で紹介したマルチチャネル信号処理のコスト関数を深層学習に用いる枠組みも開拓されている．例えば，2.3の枠組みと深層生成音源モデルを組み合わせた深層フルランク空間相関分析法などが提案されている⁽⁹⁾．

文　　　　　献

(１) Audio Source Separation, S. Makino, ed., Springer, Cham, 2018.

(２) 浅野　太，音のアレイ信号処理―音源の定位・追跡と分離―，コロナ社，東京，2011．

(３) H. Sawada, N. Ono, H. Kameoka, D. Kitamura, and H. Saruwatari, “A review of blind source separation methods: two converging routes to ILRMA originating from ICA and NMF,” APSIPA Trans. Signal Inf. Process., vol.8, May 2019.

(４) A. Hyvärinen, J. Karhunen, and E. Oja，詳解独立成分分析：信号解析の新しい世界，根本　幾，川勝真喜（訳），東京電機大学出版局，東京，2005．

(５) Ö. Yılmaz and S. Rickard, “Blind separation of speech mixtures via time-frequency masking,” IEEE Trans. Signal Process., vol.52, no.7, pp.1830-1847, July 2004.

(６) N. Ito, S. Araki, and T. Nakatani, “Complex angular central Gaussian mixture model for directional statistics in mask-based microphone array signal processing,” Proc. European Signal Process. Conf., pp.1153-1157, Budapest, Hungary, Aug. 2016.

(７) N. Ito, R. Ikeshita, H. Sawada, and T. Nakatani, “A joint diagonalization based efficient approach to underdetermined blind audio source separation using the multichannel Wiener filter,” IEEE/ACM Trans. Audio Speech Lang. Process., vol.29, pp.1950-1965, May 2021.

(８) S. Wisdom, E. Tzinis, H. Erdogan, R.J. Weiss, K. Wilson, and J.R. Hershey, “Unsupervised sound separation using mixture invariant training,” Adv. Neural Inf. Process. Syst. （NeurIPS 2020）, vol.33, pp.3846-3857, Dec. 2020.

(９) Y. Bando, K. Sekiguchi, Y. Masuyama, A.A. Nugraha, M. Fontaine, and K. Yoshii, “Neural full-rank spatial covariance analysis for blind source separation,” IEEE Signal Process. Lett., vol.28, pp.1670-1674, Aug. 2021.

（2024年6月20日受付）

(注1) math は零平均 math であると仮定する．