
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

無線通信システム研究専門委員会
Polar符号
Polar符号は,Arıkanが発表した誤り訂正符号の一つであり,通信路分極と呼ばれる現象を用いることにより定常無記憶の二元対称通信路を対象として,簡易な逐次除去復号(SCD : Successive Cancellation Decoding)を用いて,シャノン限界に漸近する特性を実現できる(1).
通信路分極は,均質な通信路を良好な通信路と劣悪な通信路に変換し,良好な通信路のみを用いることで良好な特性を実現する現象を示す.まず通信路を定義する.入力,出力アルファベットを,
とする二元対称通信路を
とし,
から
への遷移確率を
と定義する.また,通信路
を
組用いて通信を行う場合,第
通信路
の入力,出力アルファベットを
,
と表す.
次に,通信路容量を容易に計算可能な二元消失通信路(BEC : Binary Erasure Channel)を用いて通信路分極を説明する.二元消失通信路は入力に対し,出力が
となる通信路であり,
は消失(どちらが送られたか不明)を表す.このとき,
,
への遷移確率を
,
と定義する.この通信路容量は
である.
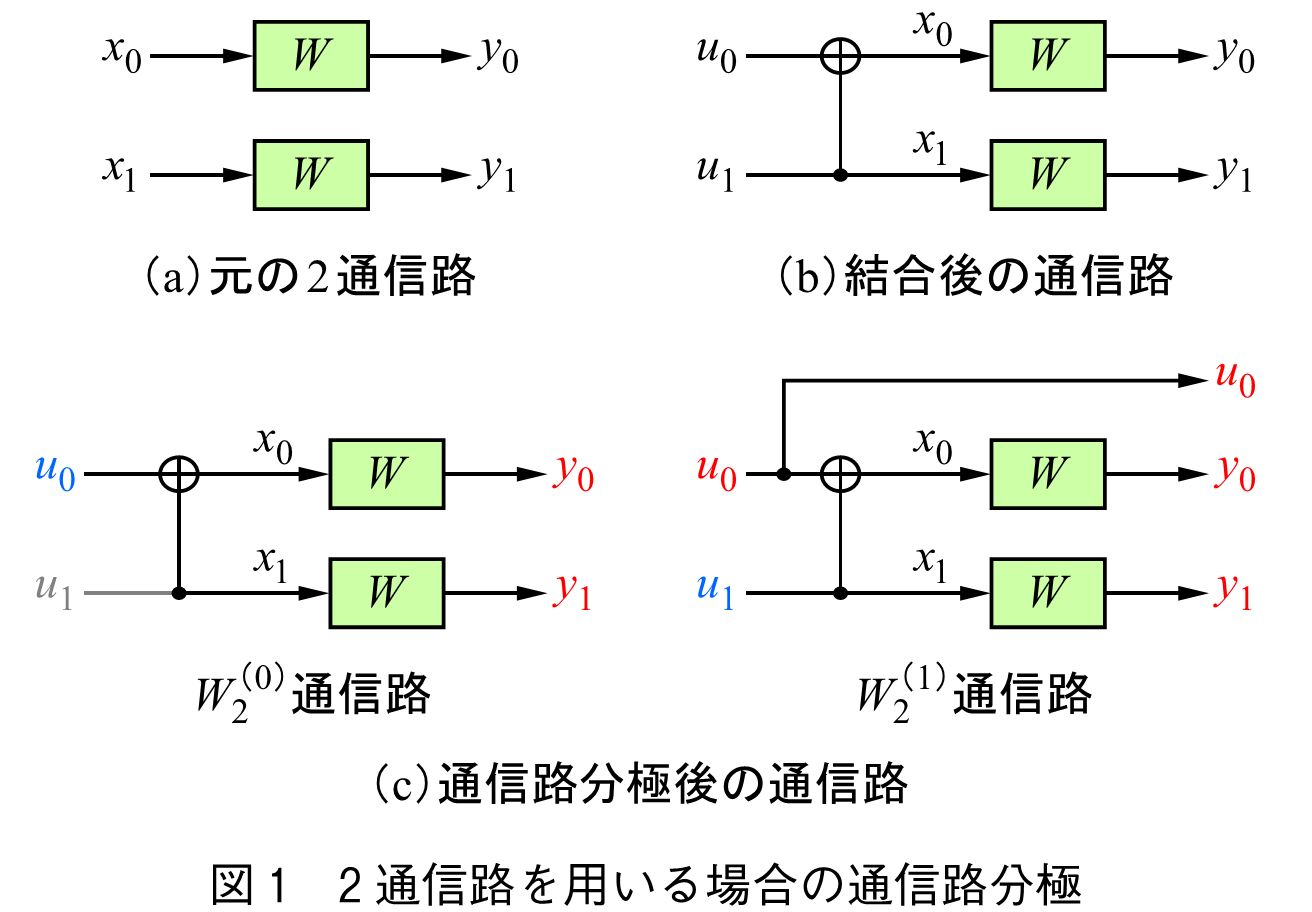
二元消失通信路を2組用いる場合について説明する.図1(a)に入力,出力アルファベットが,
の通信路
を示す.この通信路を図1(b)に示す通信路結合(Channel Combining),通信路分解(Channel Splitting)することで,図1(c)に示す2通信路
,
に変換する.それぞれの入力,出力アルファベットを図中に青字,赤字で示す.ここで,
の出力に
が含まれる点に注意が必要である.以降通信路を簡単化のため
のように記載する場合がある.
次に,この通信路の通信路容量を容量を計算する.,
通信路それぞれの入力である
,
の消失率は,表1から,
,
と計算される.消失率から各通信路の通信容量は
,
と計算される.ここで,分極前の通信路容量をを
と定義すると,以下の式が成り立つ.
(1)
(2)
式(1)は,図1(a)で示される通信路を図1(c)で示す2通信路に変換することによって,元の通信路より通信路容量が減少した通信路と増加した通信路
に変換されることを示す.式(2)は,通信路容量の総和は分極の前後で変わらないことを示す.
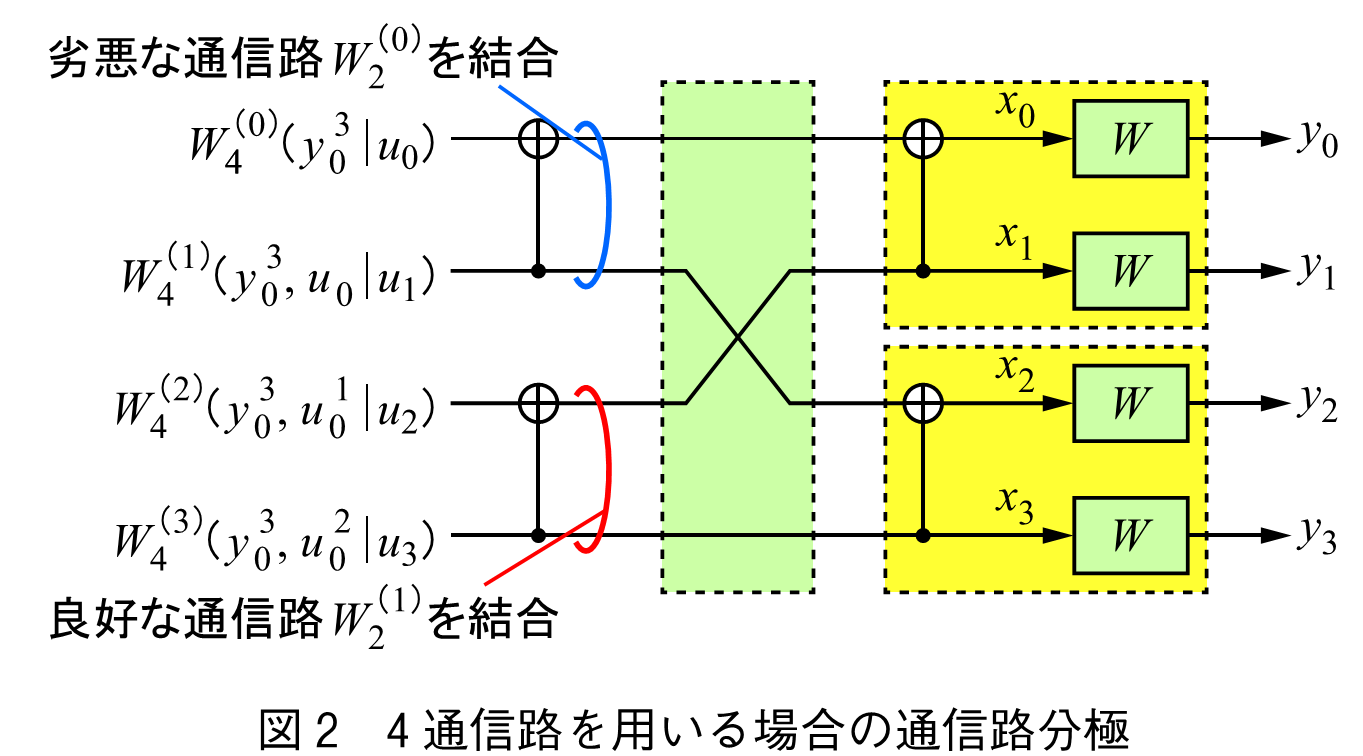
次に,これまで説明した2通信路を2組用いることによって,4通信路の通信路分極を生成する方法について図2を用いて説明する.図において,
という記載があるが,これは
,
の簡略表記である.図2に示すように,黄色で示す2組の通信路の左で薄緑で示す置換(Permutation)処理を行う.この置換処理を行うことで,その左の分極処理を行う排他的論理和の入力が均質な通信路となる.均質な2通信路に対する通信路分極処理は先ほどと同様であるため,2通信路の通信路分極処理における劣悪な通信路の消失率
を用いて,通信路
,
の消失率は,
,
として計算される.通信路
,
も
を用いて,同様に計算可能である.
以上を一般化して,回通信路分極を行った
通信路(
)を分極することで,
通信路を生成する場合について図3を用いて説明する.
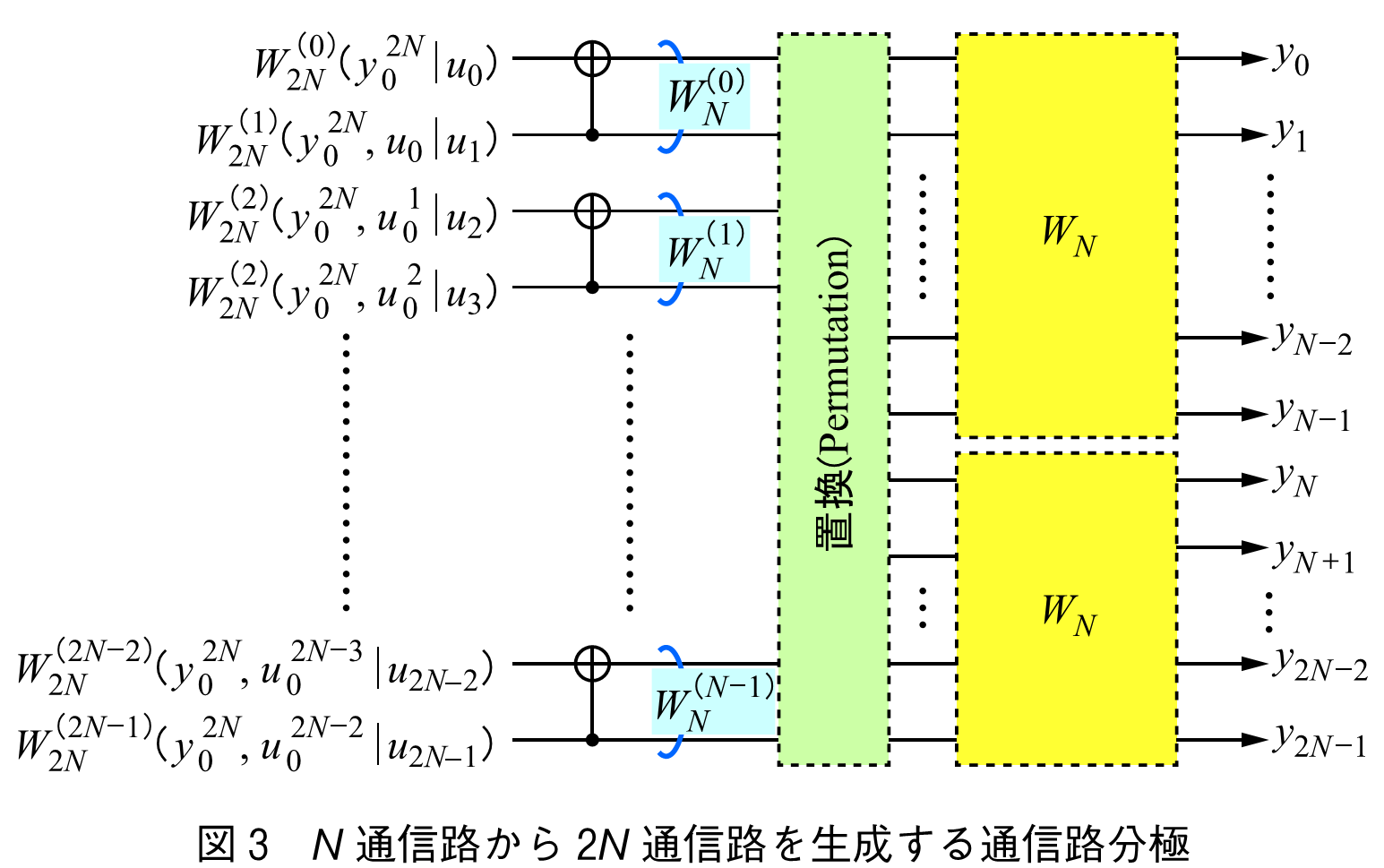
図3に示すように黄色で示す通信路
を2組を置換する.この置換は,図に示すように2組の通信路
が連続するような処理である.この均質な通信路を分極させることによって,
の通信路を生成することができる.このとき,
として,以下の漸化式により再帰的に計算することができる.
(3)
通信路の通信路容量は
を用いて計算することができる.
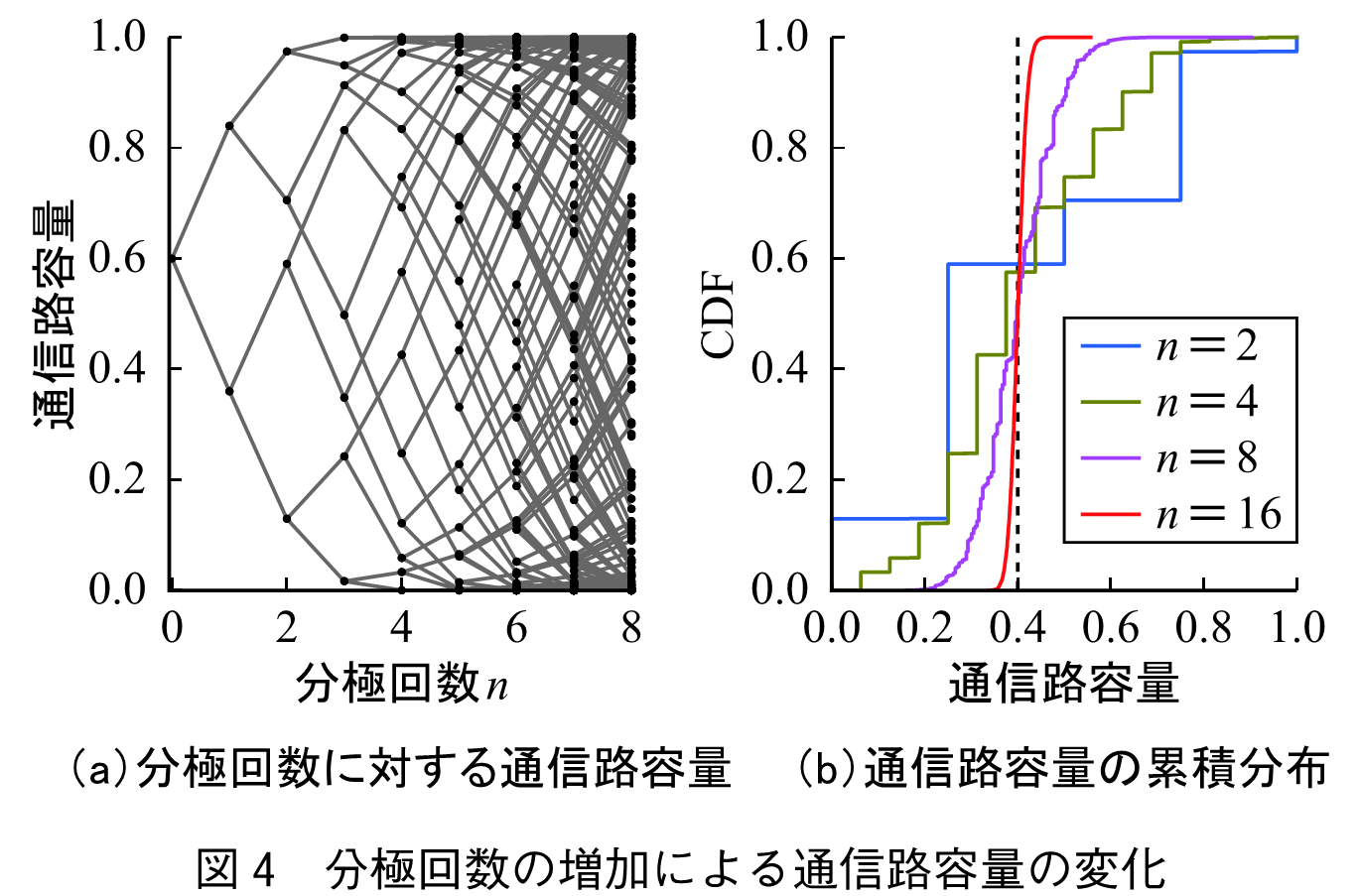
の場合について,
から8回分極した場合を示す.図4(a)において,横軸は分極回数
,縦軸は通信路容量を示す.分極回数が増加するに従い,通信路容量が0,若しくは1に漸近する.図4(a)では0,1近傍にどの程度の割合の点があるか分かりにくいので,図4(b)に累積分布特性を示す.ここでは,
の場合について示す.
の増加に伴い,通信容量0,1の割合が増加しており,その比率は4:6程度である.分極を繰り返し,通信容量が0と1のみとなった場合を考える.このとき,式(2)から通信路容量の総和は変化しないことから,通信路容量0と1の比率は
となるためである.
以上から,通信路容量1の通信路のみを用いることでシャノン容量に漸近する特性を実現することが可能である.このために,通信路容量0の通信路を送受で既知であるダミービットを用いることに相当する.このダミービットとしては0を用いることが多いが,送受で既知であれば他の値でもよい.また,Polar符号では,このダミービットのことを凍結ビット(Frozen bit)と呼ぶ.
次に,図5を用いて復号処理について説明する.図の四角で各通信路の復号器を示し,上からの矢印で示された情報を元に復号を行い,右への矢印で復号結果を示す.まず受信信号のみを用いて通信路を復号し,
を得る.次に受信信号に加え
を用いて,通信路
を復号し,
を得る.更に受信信号に加え
,
を用いて,通信路
を復号し,
を得る.これを繰り返し最終的には,受信信号に加え
,
を用いて
を得る.ここで重要なのは,これらの処理は逐次的に行う必要があることである.以上から,この復号法を逐次除去復号と呼ぶ.

この逐次除去復号では,最も通信路容量の低いを復号し,その結果に基づいて以降の通信路を復号することに違和感を感じるかもしれない.しかしながら,通信路容量の低い通信路は送受で既知の凍結ビットとすることでこの劣化を回避できる.
Polar符号は,既に第5世代(5G : 5th Generation)移動通信の制御チャネル,報知チャネルの誤り訂正符号化として採用されている(2).
この制御,報知情報には様々な情報があるため,情報ビット長は任意の長さに対して動作する必要がある.また,受信品質の非常に悪い環境から良い環境まで効率的に制御信号を通信するために,様々な符号化率を実現することが必要である.このために情報ビット長
と符号長
が決まると,符号語の生成が一意に決まる取り決め(Rate Matching)を規定し,この取り決めに基づいて送受で処理を行う.これにより
,
以外の情報を送受間で共有不要であり,制御を簡易化できる.
Polar符号では,基本的に符号長は2のべき乗の値に制限される.このため,特性を劣化させないように,符号長を調整する方法が採用されている.については,凍結ビットの割合を変更することで対応可能であるが,この順序を規定し,凍結ビットの割合を変更することで可変としている.
誌面の都合上,Rate Matchingのみを説明したが,実際には様々な工夫をしてPolar符号を5Gに適用している.
(1) E. Arıkan, “Channel polarization : A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels,” IEEE Trans. Inf. Theory, vol.55, no.7, pp.3051-3073, July 2009.
(2) 3GPP, “TS 38.212, multiplexing and channel coding, V15.13.0,” Dec. 2021.
(2024年8月27日受付)
オープンアクセス以外の記事を読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード