1．高周波漸近解法とは

　高周波漸近解法とは，電磁波の伝搬や散乱問題を解析するときに，使用する電磁波の周波数が高いこと（高周波）を念頭に置いて，波数の逆べき級数で展開（漸近展開）する形の解を求める手法を指す．

　電磁波は，電界と磁界の空間的，時間的な振動の相互作用によって，周囲に広がるが，その振動数（周波数）によってその性質や伝搬の様子がかなり異なる．また電磁波は波動性と粒子性の両方の性質を持ち，周波数が高いと光が光子と言われるように，粒子性の性質，すなわち直進性が強く現れる．

　電磁波の伝搬や物体による散乱を解析するには，電界と磁界が満足するマクスウェルの方程式から導いた波動方程式と呼ばれる微分方程式を与えられた境界条件を満足するように解く問題に帰着する．その解は，境界条件を考慮した固有モード関数の無限級数や種々の方向に伝搬する平面波スペクトルの積分表現（フーリエ積分）で表されることが多い．こうした表現は数学的には厳密であっても数値解析しようとすると，収束が悪かったり，解析的に積分が評価できないことが多い．こうした積分評価に漸近評価が有効となる．

2．振動積分の評価

　被積分関数が振幅項と位相項に十分大きな正のパラメータ（電磁波解析ではこれが波数）と位相関数の積の形：

を持つとき，積分変数の僅かな変化に対しても，位相項は激しく変化するので，その結果として被積分関数全体も激しく正負に振動する．この現象はパラメータが大きければ顕著であり，振動する被積分関数は互いに打ち消すので，積分評価が難しい．こうした積分の評価は，うまく打ち消す相手のない端点，近くからの寄与の評価が可能という考えに基づき，部分積分を繰り返して解を得ることができる（図1（a））．

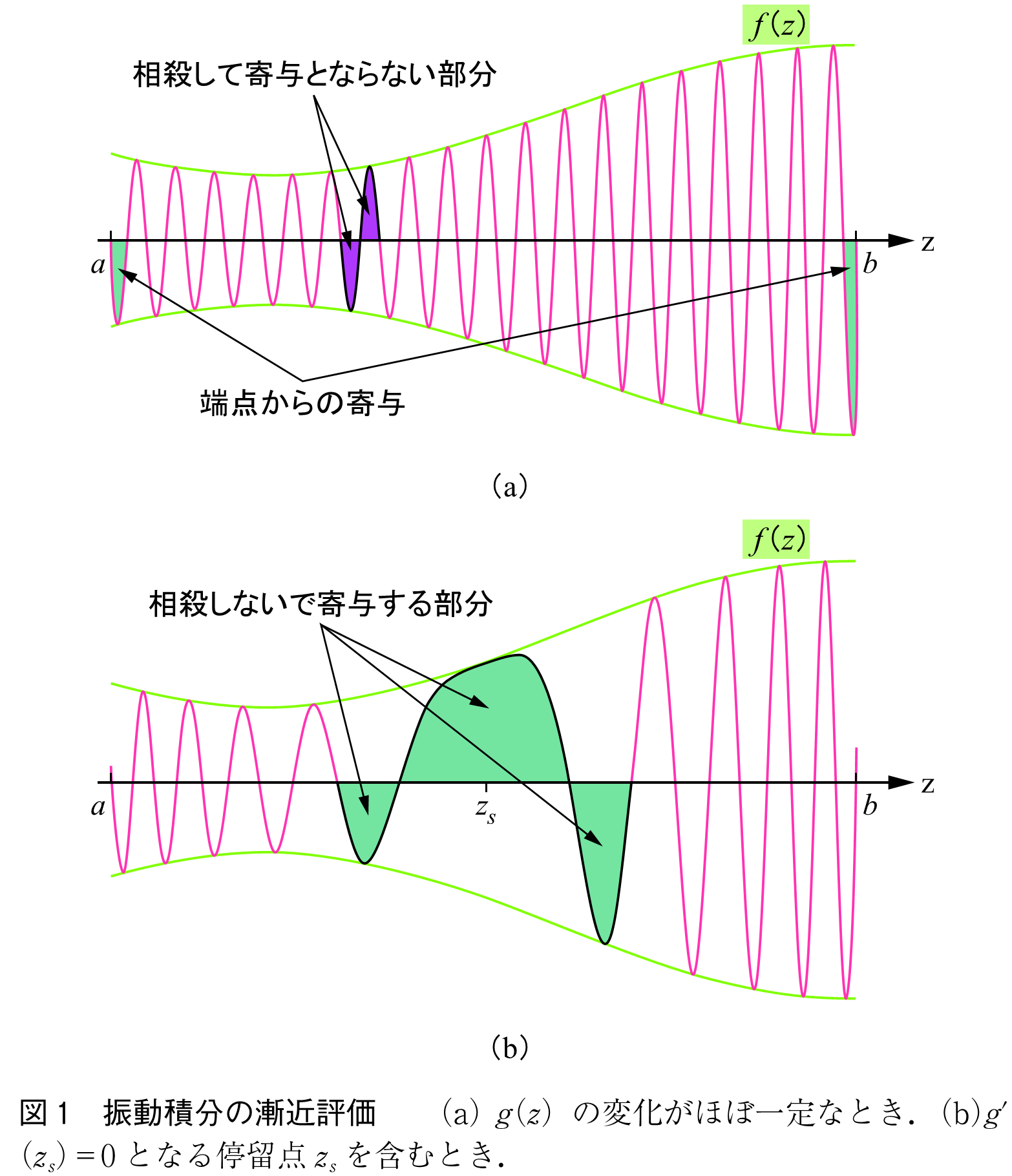
　もし位相関数が積分範囲内で導関数がゼロとなり，その変化が緩くなる点（これを停留点という）があると，その点の周りで被積分関数の振動がゆっくりになり，打ち消しが起きないので積分として寄与する（図1（b））．そこでこの停留点の周りで被積分関数を近似して評価する方法を停留点法と言う^(注1)．この停留点からの寄与は通常，端点からよりも大きな寄与となることが多い．更に被積分関数が特異点を持つ場合には，それらの影響も考慮する必要がある．

　ここでは上述した積分の近似解の導出は文献（１），（２）に譲るが，いずれの場合も次のような展開を得る．

　ここでは点における位相，はある正実数，は展開係数である．上式は，波数に対する逆べき級数展開であり，求めた展開係数は有限の波数に対しては発散する漸近展開となる^{（2）, （3）}．多くの場合には初項のみで近似することが多いが，があまり大きくないときには，高次項を入れると精度は良くなるが，更に項を増やすと逆に精度が悪くなるので，注意が必要である^（2）．

3．漸近解の適用

　例えば図2（a）のような導体円柱による電磁波の散乱問題は，固有モード関数を用いた厳密な級数展開が知られている．しかしこの解は，円柱の半径が大きかったり，観測点が遠方にあったりすると，収束が遅くて使えない．そこで解を固有関数の積分表示等を使って変形し，上述した停留点法を利用すると，これらの結果はたくさんの波の干渉の結果として図2（b）のように，観測点に到達する反射波や円柱表面に沿って進む回折波を使った解が得られる．これが高周波近似解である．こうした波は波源から出射され，伝搬，反射，透過，屈折，回折等の物理的な現象を経て観測点に到達する光線を表しているので，イメージを直感的につかむことができて種々の現象の解明に多いに役立つ．

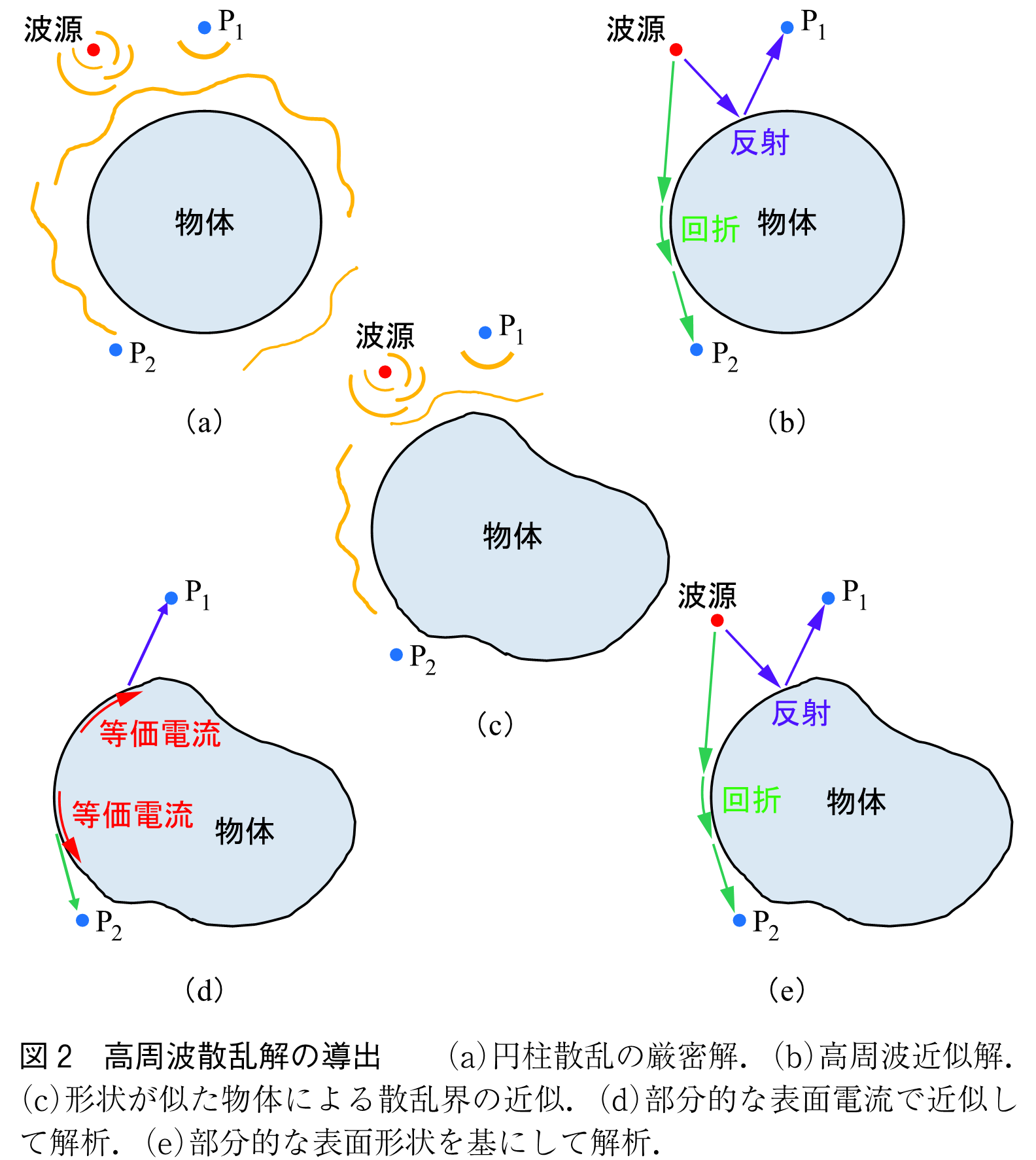
　この結果によると，反射や回折の現象は，それを生じている反射点や回折点の近くの形状によってのみ計算されている．したがって，図2（c）のように全体の形状が異なっていても，局所的な形状が似ていれば，そこで生じる現象，例えば反射や回折は同じように振る舞うと考えて解を組み立てるのが高周波漸近解法の基本となる．

　解析手法には大きく分けて以下の二つがあるが，いずれの場合にも考えている散乱体の寸法とか観測点までの距離とかが，波長に比べて大きい（波数が大きい）ことを基に導出している．

 （１）物理光学（PO）的手法

　物体からの散乱は，その物体の散乱を生じる表面近くに入射波から誘起される表面電流によって励振されるという等価定理に基づき，散乱体の表面形状に近い規範形状に誘起される電流を組み合わせて物体全体に流れる電流からの放射の形で計算する方法である（図2（d））．例えば滑らかな物体表面に誘起される誘起電流は，その表面の曲率半径が波長に比べて十分大きいなら，平板に平面波が入射した場合の誘起電流を基に放射電磁界をそれらの電流の積分から計算する．最後の積分計算は，数値積分で求めたり，解析的に電流が与えられていれば，漸近解法を使って遠方界を求めることもできる．

 （２）幾何光学（GO）的手法

　電磁波は高周波になると粒子性が強くなるので，波源から出射したレーザビーム光線の束と考え，それぞれの光線の広がりや伝搬方向を散乱物体表面の幾何形状を基に決定し，それらの光線の和の形で表現する方法である（図2（e））．反射，透過や回折を生じる各点が，それぞれ波長に比べて十分離れているので，それぞれの現象は互いに影響なく起きる前提で，規範形状による解析解の結果を組み合わせて合成界を求める．最初から光線和で計算するため，多くの光線が重なる焦点のような場所では発散して使用できない．こうした場合には，別の規範問題を解いてその結果を差し替えて用いる．

4．むすび

　最近は，高速で大容量の電子計算機のおかげで，微分方程式を差分方程式に近似して十分な計算時間と空間標本点を用意して解くFDTD（Finite Domain Time Difference，有限差分時間領域）法^（4）等があり，微細な散乱体の構造まで考慮した解析も可能になってきているが，記憶容量の限界もある．

　高周波漸近解法は元来，電子計算機のない時代に，いかに正確に解析するかという先人たちの工夫として生まれたものであるが，更なる高周波の電磁波利用が検討されている現在においてもまだ十分に適用できる手法である．

文　　　　　献

（2024年4月1日受付）