1．非線形最適化とは

　非線形最適化（Nonlinear Optimization）とは，目的関数や制約条件の少なくとも一つが非線形関数で表される最適化問題のことである．この問題は，以下のように定式化される．

ここで，は目的関数，は個の制約関数，は最適化の対象となる次元の決定変数ベクトルである．

　非線形最適化は，単一の目的関数を最適化するが，最適化する目的関数が複数ある場合，多目的最適化（Multi-objective Optimization）となる．多目的最適化は，個の不等式制約条件の下，個の目的関数を同時に最小化する次元の決定変数ベクトルを求める問題として，以下のように定式化される．

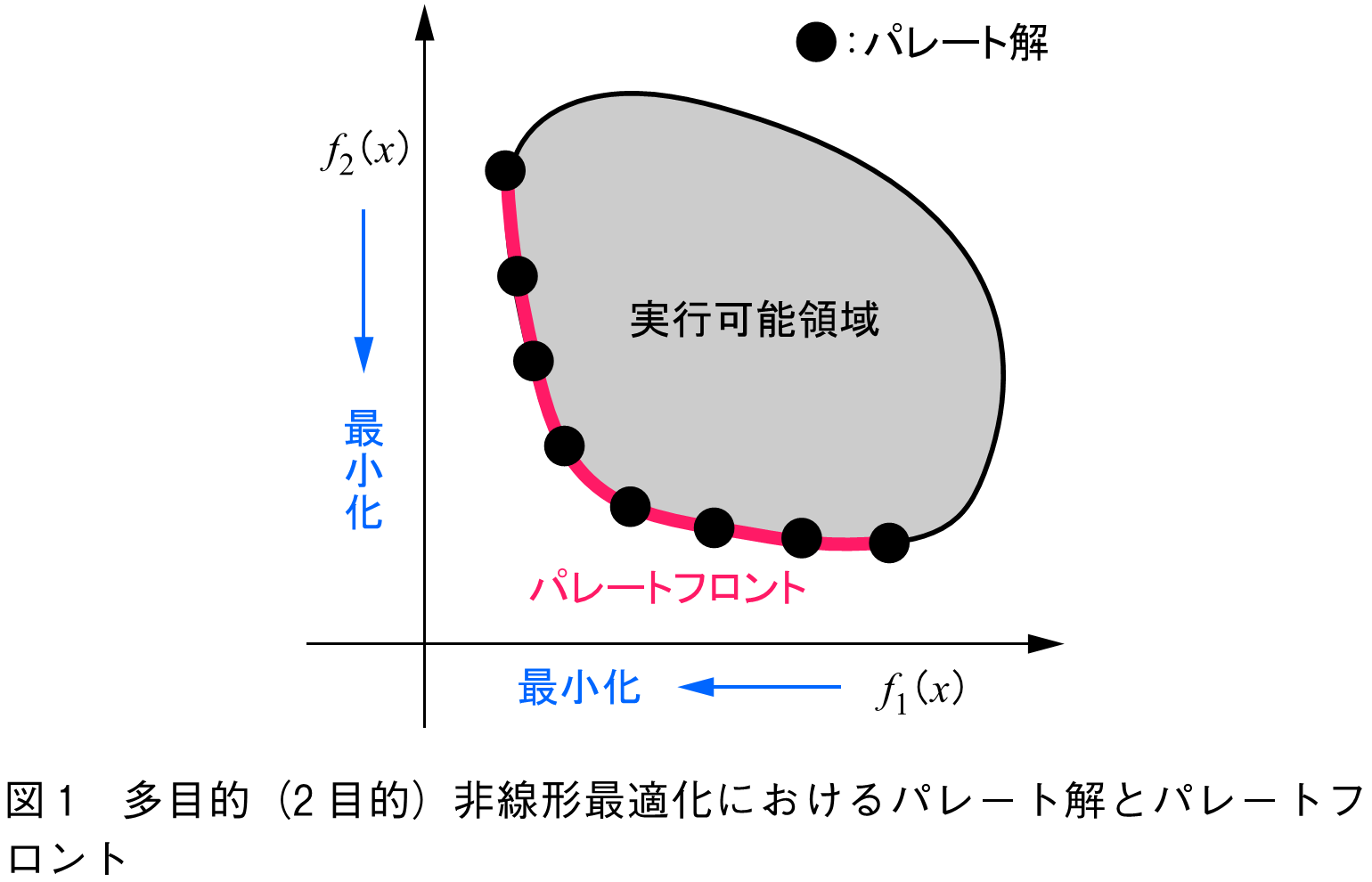
ここで，は，互いにトレードオフの関係にある目的関数である．多目的最適化では，一つの最適解が存在せずパレート解を求める．任意の解に対して，ある目的関数を一方的に改善すると，少なくとも他の目的関数の値が悪化する場合がある．このパレート解の集合をパレートフロントと呼ぶ．図1に2目的における多目的最適化問題のパレート解とパレートフロントの関係を示す．単一目的の非線形最適化は，勾配降下法，ニュートン法，内点法などを用いて最適解を探索するのが一般的である．一方，多目的非線形最適化は，パレート最適解を求めるために，群知能アルゴリズムなどの手法が用いられる．

2．進化的アルゴリズム

　進化的アルゴリズム（EA : Evolutionary Algorithm）は，生物の進化過程を模倣した多点探索手法であり，多目的最適化問題において良好なパレート解を求める方法の一つである．EAにおいて，解は個体として表現され，個体が持つ各決定変数は遺伝子と呼ばれる．また，個体の集合を集団と呼ぶ．集団は，交差や突然変異といった生物の進化過程を模倣することで，より優れたものへと進化する．

　多目的最適化に対する代表的なEAの一つにNon-dominated Sorting Genetic Algorithm II（NSGA-II）がある^（1）．NSGA-IIは，非劣ソート，エリート保存戦略，クラウディング距離を用いた手法である．を世代の親個体集合（個体数）としたとき，NSGA-IIでは以下の手順で進化処理が行われる．

1．子世代の生成

　親個体集団に対して，選択・交差・突然変異を実行し，子個体集団（個体数）を生成する．次に，親個体と子個体を統合し，という和集合を作成する．

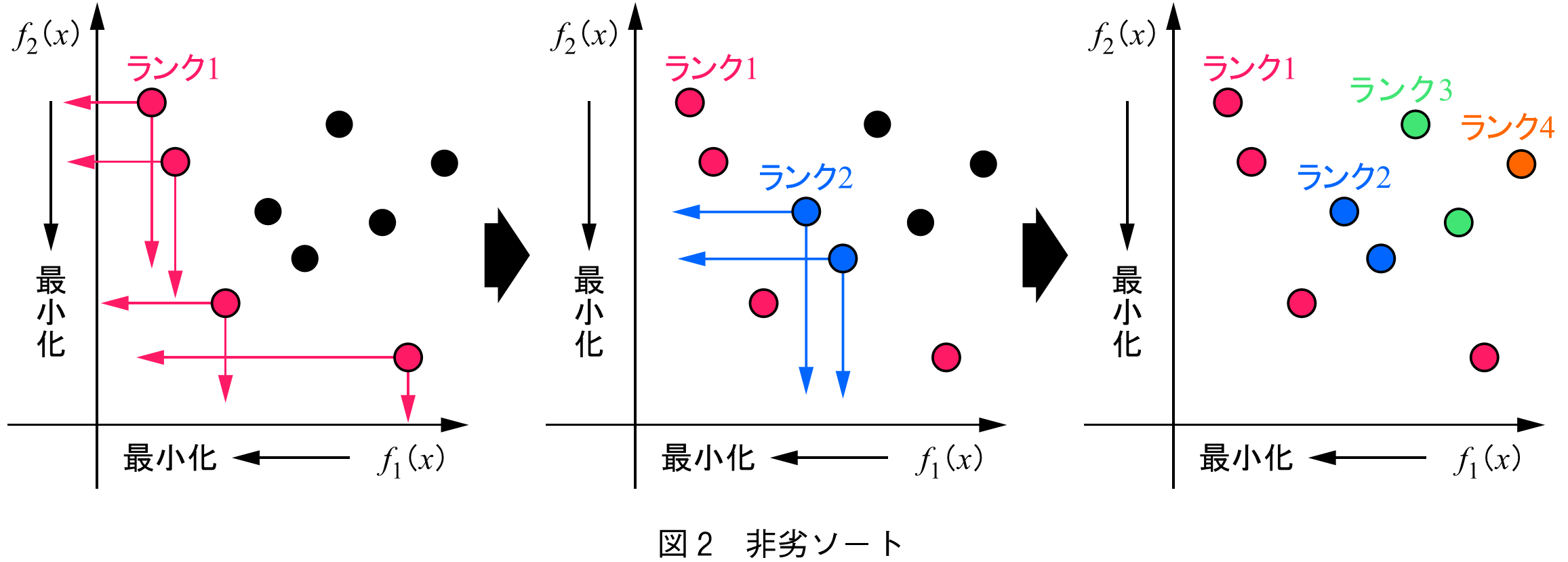
2．非劣ソート

　の各個体に対し，非劣ソートを実行し，個体間の支配関係に基づき，ランクを付与する．ここで，「個体Aが個体Bを支配する」とは，「Aが全ての目的関数でB以上であり，かつ少なくとも一つの目的関数でBより優れている場合」を指す．

　最初に，どの個体にも支配されない個体をランク1として分類する（図2）．次に，ランク1の個体にのみ支配される個体をランク2として分類する．ランクの値を一つ増やしながら，この操作を全ての個体が分類されるまで繰り返してランクを付与する．

3．エリート保存戦略

　の個体からランクが低い順に次世代の親集団を構築する．ただし，次世代の個体数がを超える場合，クラウディング距離を利用して多様性を保ちながら個体を選択する．例えば，ランク3の世代を追加中にを超える場合，ランク3の個体はクラウディング距離の値が大きい順に次世代集合に追加する．

　クラウディング距離は，各個体が他の個体とどれだけ離れているかを示す指標であり，多様なパレート解を得るために重要である．距離が大きい個体ほど他の個体と離れているため，多様性を確保するための優先度が高くなる．クラウディング距離が大きい個体から順に，個体数になるまで追加する．

　これらの手順を繰り返すことで，NSGA-IIはパレートフロントに近い解を探索する．更に，NSGA-IIの改良版として，NSGA-IIIが提案されており，3目的以上の高次元多目的最適化問題に対応できるようになっている^（2）．

3．差分進化法

　差分進化法（DE : Differential Evolution）は，個体間の差分を利用して新たな個体を生成する最適化手法である^（3）．この手法は，単目的最適化問題において特に高い探索性能を発揮し，連続最適化問題に広く適用されている．DEの基本操作は，以下の三つのステップで構成される：

突然変異　個体ベクトルを変異させ，新しい候補解を生成する．

交差　変異個体と親個体を交差し，新たな子個体を生成する．

選択　子個体と親個体を比較し，より良い個体を次世代に引き継ぐ．

　DEの特性を生かした様々なアルゴリズムが提案されているが，その中でもSHADE（Success-History based Adaptive Differential Evolution）は，成功履歴に基づいてDEの主要な二つのパラメータであるスケーリングパラメータと交差率を適応的に調整する手法である^（4）．SHADEは，従来のDEと比較して効率的な探索性能を持つ優れた手法である．

　探索個体群に対する，SHADEの動作について説明する．まず，突然変異では，三つの個体ベクトルを用いて新たな変異個体を生成する．SHADEにおける突然変異は以下の式で定義される．

ここで，は，上位個体の中から無作為に選ばれた優良個体である．は個体群から無作為に選択された個体，は個体群と探索の過程で淘汰（削除）された個体を保存したアーカイブ個体群の和集合から無作為に選ばれた個体である．がスケーリングパラメータで0＜≤1の値を取る．

　次に，変異個体と探索個体を用いて，以下に示す式に従い交差を行うことで進化個体を生成する．

ここで，は無作為に選ばれた設計変数次元，rand［0, 1）は，0以上1未満の一様乱数である．もし，乱数値が交差率以下，または，ならば，進化個体の番目の設計変数は変異個体のものとなり，そうでなければ探索個体のものとなる．

　群知能アルゴリズムには様々なパラメータが存在し，効率的に解を探索するためには，問題の性質に応じた適切なパラメータ値の設定が必要である．SHADEでは，パラメータ値を適応的に設定するため，各世代でとなる進化個体が得られた際，その個体を生成する際に使用したとの値を，それぞれまたはに保存する．その後，保存された及びを基に複数の適応制御パラメータ値を算出し，履歴メモリに保持する．探索個体の進化処理を行う際には，履歴メモリから無作為にパラメータ値を選択し，その値を用いて新たなとの値を決定する．この適応的パラメータ設定により，探索の多様性と収束性のバランスが保たれ，より効率的な探索が可能となる．また，集団サイズを線形的に減少させることで，計算コストを削減したL-SHADE^（5），L-SHADEの適応的パラメータ戦略を強化したiL-SHADE^（6）も提案されている．

4．まとめ

　非線形最適化は，非線形な制約条件や目的関数を扱うため，多くの応用分野で取り扱われる．そのため，非線形最適化問題を解く高速かつ高性能なアルゴリズムの開発は重要な役割を果たす．

　単目的非線最適化問題や多目的非線形最適化問題の解法は，勾配情報を基に解を探索するニュートン法，準ニュートン法，内点法などがあるが，本稿では，勾配情報が得られない問題や制約条件が複雑な問題に対して有効である，群知能アルゴリズムを取り扱った．

文　　　　　献

（2025年2月20日受付）