
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|
解説
エンジニアのための脳科学のすすめ
Introduction of Neuroscience for Engineers
abstract
脳と人工知能を対比しながら,知能のメカニズムを考察する.脳の特徴は,超複雑ネットワーク構造,大規模なファンイン/ファンアウト構造,自発活動の生成など,従来の計算機とは本質的に異なる.このような特徴を生かした脳の計算原理として,リザバー計算と神経ダーウィニズムを紹介する.リザバー計算では,課題解決のためにネットワークを最適化するのではなく,ネットワークのダイナミクスを利用する.神経ダーウィニズムでは,多様な活動パターンを自律的に創り,そのパターンを必要に応じて利用する.これらの生物や脳に学ぶ自律化技術は,人工知能が苦手とする課題を克服するために,今後ますます重要となると考える.
キーワード:脳,リザバー,ダーウィニズム,自律性,ニューラルネットワーク,コネクショニズム
筆者は,工学部機械系学科に所属しながら,脳の研究を進めてきた.その動機は,脳の計算原理を明らかにし,「知能」を宿す計算機を作ることにある.きっと同胞の工学系研究者や企業エンジニアはいるはずだと信じているが,脳(神経科学)の専門家が集う学会では,残念ながら同胞に出会えることは滅多にない.
歴史的には,パーセプトロン(1),ネオコグニトロン(2),コネクショニズム(3),(4)など,著名な人工ニューラルネットワークの理論的な研究は,神経科学の実験的な研究とともに発展してきた.最近の人工知能の研究も,深層学習をはじめ,人工ニューラルネットワークの研究に多大な影響を受けている.しかし,神経科学の実験的研究と人工知能が互いに影響を与え合っているかと問えば,筆者の実感として,両者の交流は現在のところ極めて少ない.
その理由の一端は,現在の人工知能の計算原理は,言うまでもなく,脳の計算原理とは異なることにある.人工知能で用いられる学習アルゴリズム(例えば誤差逆伝搬法)が,実際の脳の神経回路に実装されている可能性はありそうもない.そうすると人工知能と神経科学の交流も遠のく.また,計算原理だけでなく,思想や言語も違うかもしれない.そもそも人工知能の「知能」とは何だろうか.それは,筆者をはじめ,神経科学者が解明せんとする「知能」と同義だろうか.筆者は,脳が生み出す知能を「生命知能」と呼んでいる.本稿では筆者らの研究に基づいて,人工知能と対比しながら生命知能の本質を考えたい.
エンジニアリングとは,実現したい機能から出発して,そのためのメカニズム,構造,手法などを決定し,具現化していくプロセスである.逆に,既存の機械やシステムを調べ,それが実現しようとする機能を解き明かすプロセスが,リバースエンジニアリングである.そのように考えれば,脳を対象にしてリバースエンジニアリングできる(5),(6).例えば脳の構造から出発して,脳が生み出す「知能」という機能を解き明かせばよい.
脳のリバースエンジニアリングの一例として,1980年代に発展したニューラルネットワークの研究が挙げられる.ニューラルネットワークに基づいて認知や行動のモデルを構築する研究は,コネクショニズムとか,コネクショニストモデルと呼ばれた(3),(4).高速な計算素子で命令を逐次実行するノイマン形計算機とは異なり,脳は,数msのオーダでしか動作できない低速な計算素子を利用して,非同期的に並列計算を実現している.経験的には外部刺激の入力から認知や行動出力までの時間は数百msなので,素子レベルで1ステップ(シナプス)の計算時間が数msであることを考慮すると,脳は入力から出力まで100時間ステップ(数百ms/数ms)のオーダで計算していることになる.この概算は,コネクショニズムでは「100時間ステップ(100 time step)」問題として知られている(3).この問いに対して,コネクショニズム研究者(コネクショニスト)は,ノイマン形計算機とは異なる計算方法を探求した.
しかし,コネクショニズムでも,脳の巨大なネットワークや複雑な構造がニューラルネットワークに忠実に再現されているわけではなかった.例えば,実物の大脳皮質には100億個の神経細胞があり,細胞間をつなぐ脳内の配線長は,10万kmにも及ぶという試算もある.複雑な配線により,各神経細胞は,103から104個もの神経細胞から入力を受けたり,出力したりしている(7).このような大規模なファンイン/ファンアウトの構造を実装できるほど,従来のニューラルネットワークは大きくない.人工的な計算機でも,103から104のファンイン/ファンアウトの構造は技術的に不可能である.また,実物の脳は自律的に活動している.この自発活動は,外部からの刺激で生じる誘発活動をはるかにしのぐと言われている.このような脳の特徴も,コネクショニズムでは考慮されなかったし,従来の計算機に実装されるはずもない.
このような相違にこそ,脳の計算原理が隠されているはずである.例えば,一つの神経細胞が104個ものシナプス入力を受けているとすれば,個々のシナプス伝達は些末であり,多数のシナプス入力の同期が重要であると考えられる.恐らくこのような工夫により,個々の素子の信頼性は低くても,システム全体としては頑健な計算を実現している.また,ある神経細胞がシナプスを介してつながっている神経細胞数は,1シナプスでは104個のオーダ,2シナプスでは108個のオーダ,3シナプスでは1012個のオーダと概算できる.(簡単のため冗長性を排した.)大脳皮質には神経細胞数が100億個しかないので,ある神経細胞が活動電位を発生した後,その情報は数シナプス(数ステップ)を介して自分に戻ってくる.このような概算から,脳の情報処理は極めて再帰的であることが分かる.100時間ステップ問題に脳の情報処理の再帰性を考慮すると,入力情報は100時間ステップで脳内を30回(100ステップ/数ステップ)も周ることになる.このことから筆者は,100時間ステップ問題を30周問題と捉え直したい.30周問題では,脳の安定した同期特性が決定的な影響を与えるはずである.
超複雑ネットワーク,大規模なファンイン/ファンアウト,自発活動,30周問題など,脳の特徴は,従来の計算機とは本質的に異なるが,進化で得られた設計解である.これらが,どのような計算方法や機能の実現に資するかを理解することは,脳科学分野だけでなく,次世代の計算機開発にも有用な示唆を与えるはずである.
コネクショニズムでは,ニューラルネットワークの学習アルゴリズムとして,誤差逆伝搬法が確立された(8).この手法は,目標値に対する出力誤差を最小にするように,勾配降下法により,ネットワーク内のパラメータを出力層から入力層へ向かって順次調整する.しかし,大きなネットワークでは,入力層側では勾配が消失し学習が進まないことや,勾配降下法に伴う不安定性により解の収束に時間が掛かることが問題点として認識されている.また,誤差逆伝搬法は,数学的なアルゴリズムとしては画期的だが,実際の脳への実装には現実的ではない.例えば,誤差逆伝搬法は,ネットワーク内の「全ての」パラメータを調整するが(図1(a)),そのような調整は脳では恐らく不可能である.先に述べたように,脳内には100億個もの神経細胞があり,各神経細胞の入出力パラメータは103から104に上る.何かを学習するたびに,これらの全てのパラメータを同時に更新するとは到底考えられない.
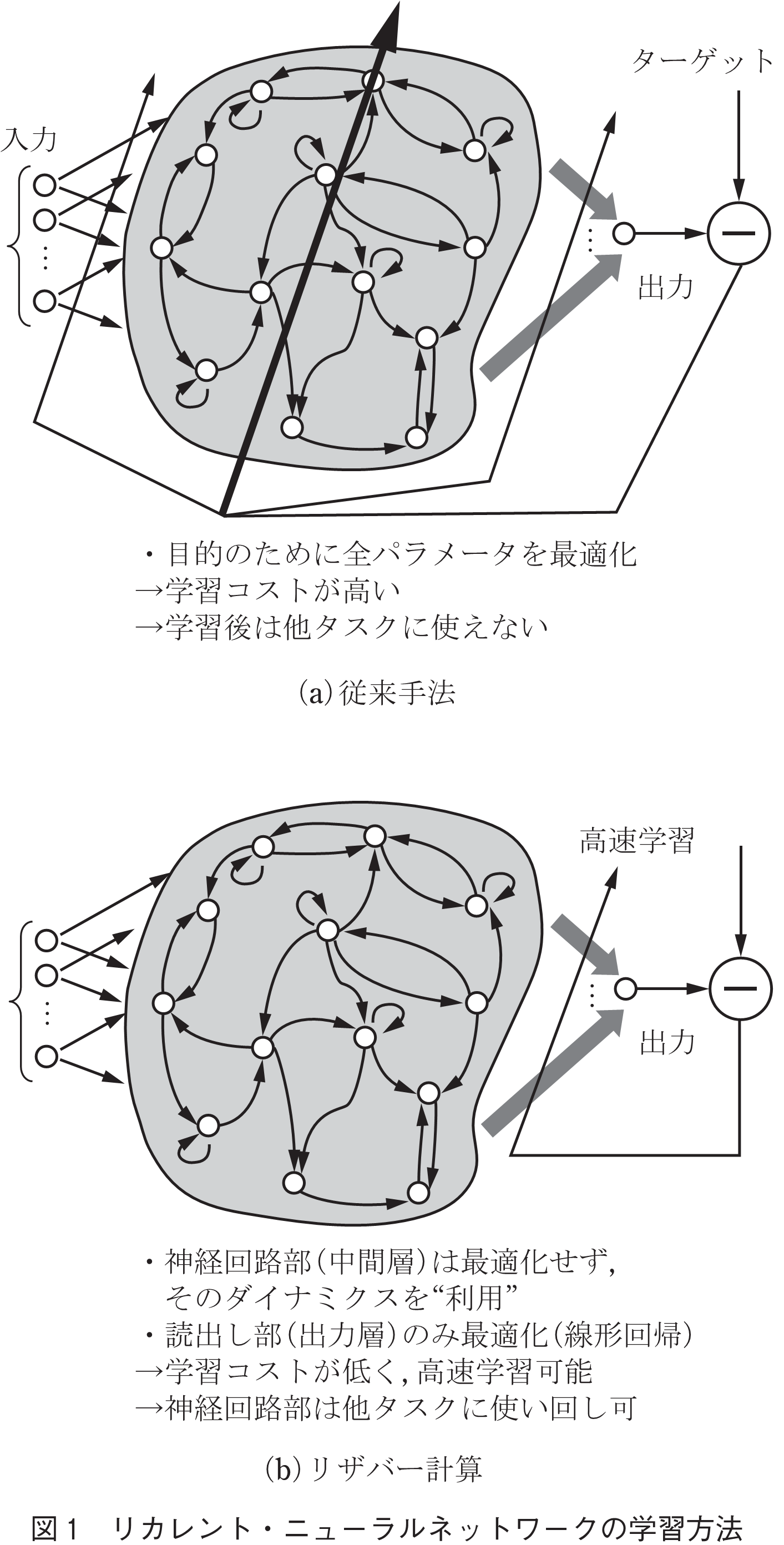
筆者らは,もっと現実的な脳のモデルとして,「リザバー計算」に注目している(9),(10).リザバー計算は,Liquid State Machine(11)やEcho State Network(12)を先駆けとして発展し,最近では,大規模なリカレント・ニューラルネットワークの学習手法として神経科学業界でも注目されている(13),(14).誤差逆伝搬法とは異なり,リザバー計算では,各ニューロンの出力の「読出し部(出力層)だけ」を調整し,最適な出力を得る(図1(b))(9).すなわち,リザバー計算では,課題解決のために,ネットワークを最適化するのではなく,ネットワークの非線形なダイナミクスを利用する.このような学習方式のメリットは,第1に,調整しなければならないパラメータの数が,非常に少ないことにある(素子数のとき,計算量は
ではなく
に比例).したがって,大規模なネットワークでも,爆発的にパラメータ数を増加させることなく,高速な学習を実現できる.第2に,ネットワークのダイナミクスは,任意のタスクに利用でき得る.したがって,一つのネットワークを使い回し,複数タスクの実行や,様々な状況・環境下でのタスク遂行を実現できる.一方で,誤差逆伝搬法のような従来手法では,特定の目的の下,ニューラルネットワークの入出力関係を厳格に決めてしまうので,学習後のネットワークは,当然ながら当初の目的以外のタスクには利用できない.脳は一つしかないのに,様々なタスクを遂行できることを鑑みれば,脳の計算原理として,リザバー計算の枠組みが理にかなっていると筆者は考える.
リザバー計算の研究トレンドでは,どのようなダイナミクスに,どのような計算能力が宿るのかという理論的研究が盛んになっている.直感的に言えば,ニューラルネットワークが豊かなダイナミクスを生成できなければ,難しいタスクを解決できなくなる.また,筆者らの考えでは,脳の動作原理は「神経ダーウィニズム」にある(15),(16).すなわち,脳は,時空間的な神経活動パターン(ダイナミクス)の多様化と自然選択により,適応的な情報処理を実現している.したがって,脳の創発特性には,様々な時空パターン(ダイナミクス)として記憶を作り,神経回路内に維持すること,そして,必要に応じて適切な記憶を検索・利用することが不可欠であると考える.
生命知能の創発メカニズムを探った筆者らの試みとして,リザバー計算に着想を得た神経細胞の分散培養系の身体化実験を紹介したい(17).
ラットの胎児から神経細胞を取り出し,それをシャーレの上に播種し培養すると,やがて培養神経細胞は互いにコミュニケーションを取るようになり,自己組織的に神経回路を形成する.筆者らは,培養神経回路をリザバーと考え,その自発的な活動パターンを利用した創発的バイオコンピューティングの実現方法を考察した.具体的には,混沌とした自発活動パターンから秩序ある出力パターンを取り出すことを試みた.
実験試料として,ラット大脳皮質に由来する神経細胞を微小電極アレー上に分散培養した(18),(19).神経回路から生成される自発活動パターンは,回路の成熟に伴い複雑になる(20).このような培養神経回路を身体化することを考える.すなわち,培養神経回路をパターン生成器として利用し,生成パターンに応じて,移動ロボットを制御する.制御信号は,各神経細胞の活動量に重みを乗じ,それらの線形和(スカラ値)とする.身体化されたロボットは,神経回路の自発的な活動パターンから作られた制御信号で動き回るようになる.
次に,各時刻において,制御信号の振幅に比例するフィードバック刺激を全ての神経活動に与えることを考える.(ただし,その比例定数は細胞ごとに異なる.)この閉ループ系において,FORCE(First Order Reduced and Controlled Error)学習により(21),制御信号が任意の目標値と一致するように,各神経細胞活動量に乗じた重みを最適化する.なお,最適化の対象は,神経回路の読出し部だけであることに注意されたい.また,フィードバック刺激には,光照射により生理活性を制御できるケージド化合物を利用した.光源にはレーザを用い,ディジタルミラーデバイスにより任意の光パターンを照射した.ケージド化合物としてシナプス伝達物質を用いれば,この装置により神経回路の活動を空間的に制御できる(図2(a)).
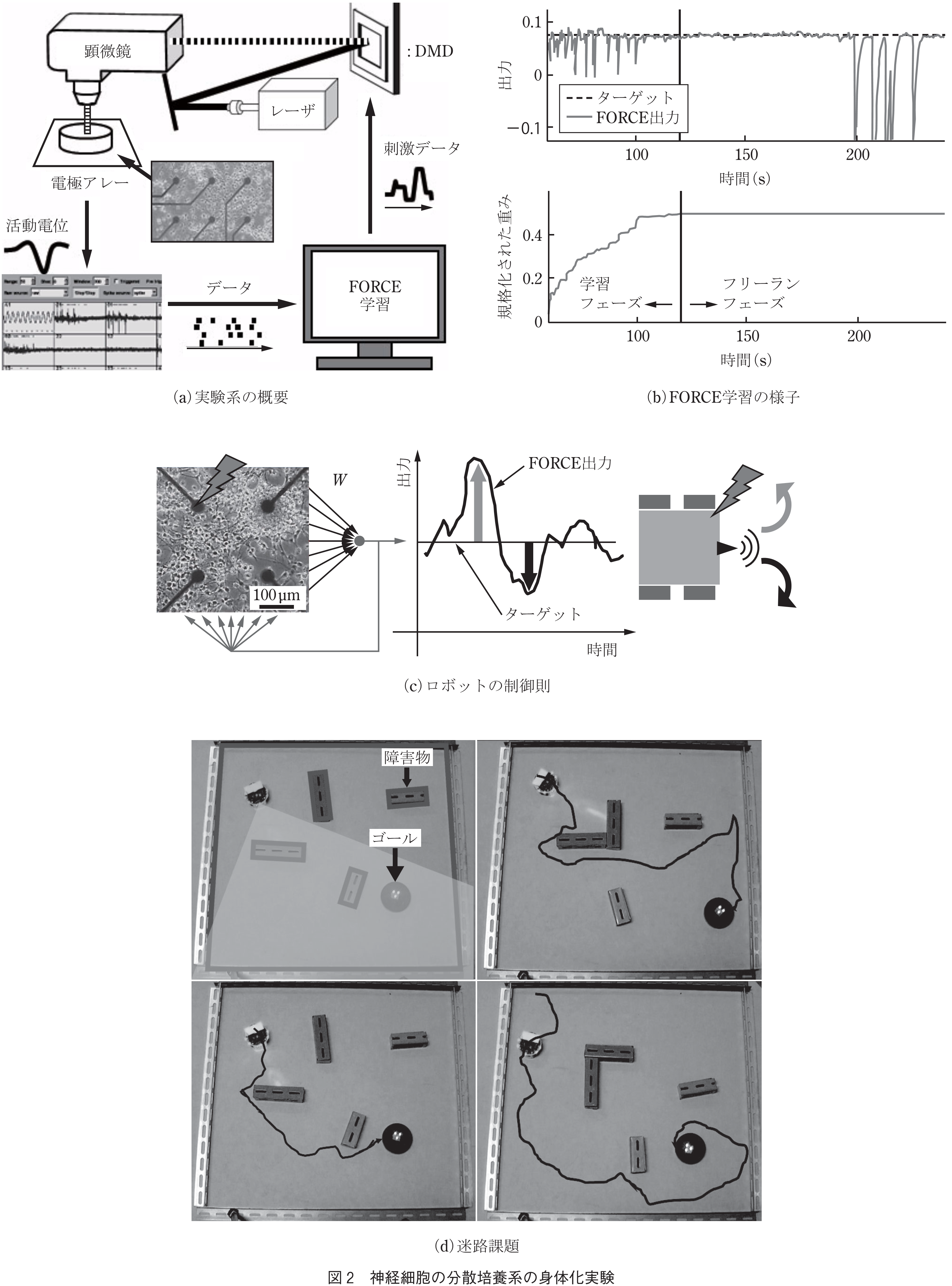
FORCE学習で適切な重みが求まれば,閉ループ系では制御信号は,実験者が設定した任意の目標値となる(図2(b)).一方で,フィードバック刺激を止めて開ループにすると,制御信号は自発活動に応じて生成されるようになるため,実験者から見れば無秩序になる.すなわち神経回路は,フィードバック刺激により,混沌とした無秩序な状態から秩序ある状態に遷移する.
このような状態遷移を移動ロボットの行動で定性的に可視化することを試みた.ロボット制御では,神経回路からの出力値と目標値の誤差に基づき,車輪の利得を決めた.誤差がゼロの場合,ロボットは直進するが,実際には誤差に応じて揺らぎながら直進する(図2(c)).ロボットが直進できるようになると,簡単な迷路課題を解決できるようになる.例えば,ロボットの進行方向から±45°の範囲にゴールがある場合は直進する.この範囲からゴールが外れた場合(ロボットがゴールを見失った場合),またはロボットが壁に接触した場合,培養神経回路に電気刺激を印加し,外乱を与え,強制的に方向転換させる.非常に簡単なアルゴリズムではあるが,これによりロボットはゴールに到達できるようになる(図2(d)).このようにして,揺らぎを利用して行き詰まりを回避しながら,目標地点に到達する戦略は生物の常とう手段である(例えば文献(22),(23)).
さて,ここからは極めて主観的ではあるが,筆者は,培養神経回路で身体化されたロボットが動いている様子には生命らしさを感じ,迷路を解く様子には賢さを感じてしまう.ここで注意すべきは,生命らしさ(生命性)も賢さ(知性・知能)も,厳密に定義されているわけではなく,観察者が勝手に「感じる」性質である.生命性を感じさせる要件は,恐らく,生物特有の揺らぎにある.脳の自発活動も,その起源は,熱揺らぎによるイオンチャネルの開閉と考えられる.一方で通常の電子機器は,揺らぎ(雑音)に影響されずに動作するように設計されている.したがって計算機や人工知能システムには,自発活動は存在しない.そのため,これらの人工システムには生命性を感じない.
知能を感じさせる要件は更に主観的である.ロボットの軌跡を見れば分かるとおり,ロボットの行動は迷路課題の最適解ではない.したがって,最適解を導けるかどうかは,知能とは関係ない.(ただし,人工知能に対して感じる賢さには,最適近傍解の導出が要件に含まれるかもしれない.)筆者の考えでは,生命性を有するシステムの場合,混沌とした状態から秩序ある状態が作り出されるとき,そのメカニズムに知能を感じる.脳では多様な活動パターンを自律的に創り(混沌を生み出し),そのパターンを必要に応じて利用する(秩序を創る)戦略,すなわち神経ダーウィニズムが,知能の起源であると考える.これを筆者は生命知能と呼んでいる.
脳の生命知能をリザバー計算の枠組みで考えるならば,神経回路の特徴の精査が重要な研究テーマとなる.興味深いことに,神経細胞の分散培養系は,自己組織的に神経回路を形成する.神経回路構造の複雑化と伴い,時空パターンも複雑になる.シナプス結合強度や発火頻度の分布,時空パターンの多様性や再現性,自発・誘発活動のダイナミクスの関係性などが,リザバー計算の性能へ影響を与え得る(20).また,脳の特長として,階層的または状況依存的な記憶の生成や想起が挙げられるが,その特長も脳の時空パターンで実現されている(19),(24).このような神経回路の特徴には,不完全で雑音を含むデータによる学習や,時々刻々と変化する状況(コンテクスト)へのリアルタイム処理,非同期的に得られるマルチモーダルな情報処理など,人工知能が苦手とする課題を解決するヒントが隠されているかもしれない.
脳の大脳皮質の情報表現では,機能マップと神経反応の同期の機能的意義が古くから議論されてきた.機能マップの例として,大脳皮質では,視覚,聴覚,運動,体性感覚など,機能ごとに領野が分かれている.更に運動野には身体マップがあり,運動野の各部位は,手,足,顔など,特定の身体部位の運動機能を担っている.このような機能の明確な分担がある一方で,脳の並列計算では,複数の神経細胞の協調作業や複数領野の連携も欠かせない.そのために同期が利用されていると考えられている.筆者らは,機能マップと同期は,それぞれ,混沌を生み出す戦略と秩序を創る戦略に利用されているという仮説を立てて,その検証をラットの聴覚野の生理実験で進めてきた.
聴覚系では,音情報は周波数成分に分解されて処理される.音情報は蝸牛で神経信号に変換されるが,蝸牛の各部位は,特定周波数の振動に反応するため,蝸牛には空間的な周波数マップが形成される.周波数マップは,上位の中継核にも引き継がれ,聴覚中枢の情報処理に重要な役割を担うと考えられている(25).
聴覚系の最上位の聴覚野でも,明確な周波数マップが認められる.その機能的な意義として,二つの仮説が考えられる.第1の仮説は,重要な情報の表現は,必要以上に多くの神経細胞が冗長的に動員されることで,頑健な情報表現を実現している可能性である.第2の仮説は,神経細胞の情報表現は冗長的ではなく,むしろ,周波数マップの面積が神経細胞の多様性を反映している可能性である.
筆者らは,ラットの聴覚野を対象とし,上記の二つの仮説の妥当性を検証した(16).ラットの聴覚野の各神経細胞は,特定の音の周波数に対する選択性を示す.そこで,同じ周波数選択性を示す細胞を集めて精査したところ,各細胞の反応特性は様々であることが分かった(図3(a)).これらの反応特性を刺激と発火数の相互情報量で定量化したところ,神経細胞の反応特性の多様性が周波数マップ上の面積と密接に関係した.すなわち,周波数マップ上で広い面積を占める部位では,神経細胞の反応特性は豊かな多様性を示し,逆にマップ上の狭い部位では画一的な細胞が多いことが分かった.なお,聴覚野で広い面積を占め,豊かな多様性を示す部位は,高い周波数(超音波)領域だった(図3(b)).これは,ラットが超音波帯域でコミュニケーションしているため,その領域がラットにとって重要であるからだと示唆される.
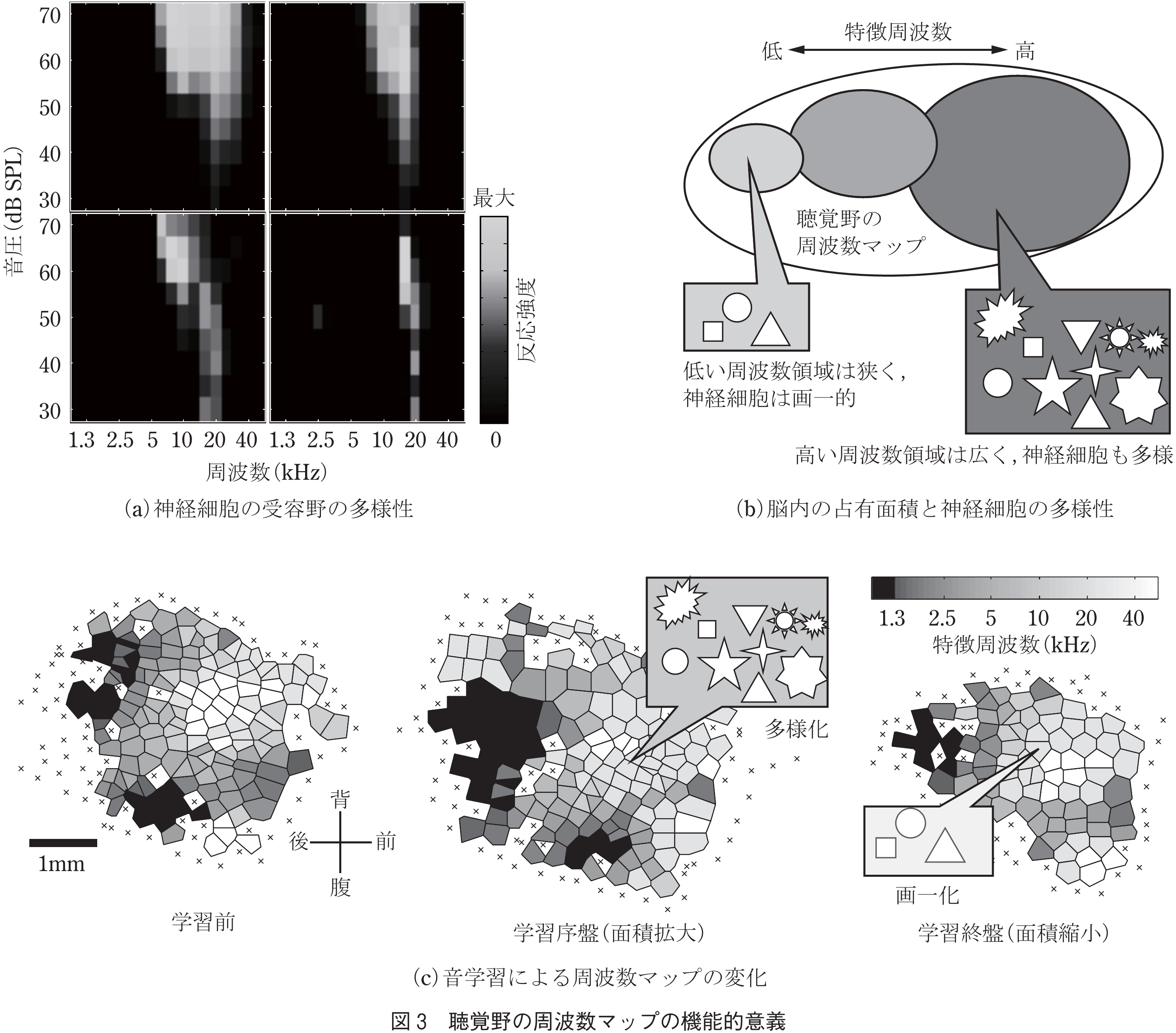
機能マップは学習や経験に応じて柔軟に変化することも知られている(図3(c)).そこで,このような機能マップの変化に応じて,神経細胞集団の多様性が変化するかを調べてみた.実験では,特定の音が提示されたときに,ラットがスイッチを押すと,報酬として餌が与えられるという学習を1か月間続けた.その結果,ラットが試行錯誤を始める学習途上では,聴覚野で音に反応する神経細胞が増え,それに伴い,細胞集団の多様性も増加した.一方,学習終盤では音に反応する神経細胞が減り,その多様性も減じた.
これらの結果から脳にとっての学習とは,多くの神経細胞を情報処理に参加させて神経活動の多様性を増やすことで,効率的に解を発見することであると示唆される.また学習とは,一旦,解を発見した後,無駄な神経活動を排除し,効率的な情報処理を獲得していくことであると解釈できる.
多様な神経細胞が,豊かな知覚の世界の基盤であることは疑いない.しかし,多様な細胞が無秩序に活動すれば,知覚の世界も秩序を失う.多様な神経細胞が秩序ある知覚を作り出すためには,同期が重要な役割を担っていると考えられる(26).
聴知覚には,任意の純音を組み合わせて和音を作ると,協和音や不協和音のような音響学的な質感に加え,長調や短調のような情動的な質感が生まれる(27).これらの聴知覚や学習には,聴覚野だけでなく,前頭前野,扁桃体,線条体など様々な領域との相互作用が欠かせない.そのような相互作用には,脳の定常的な同期特性に影響されると考えた.そこで本実験では,聴覚野の定常的な位相同期パターンに注目した.具体的には,30秒間の連続音を提示しながら聴皮質内の局所電界電位を多点同時計測し,任意の電極ペアで帯域ごとの位相同期を調べた(図4(a))(28).
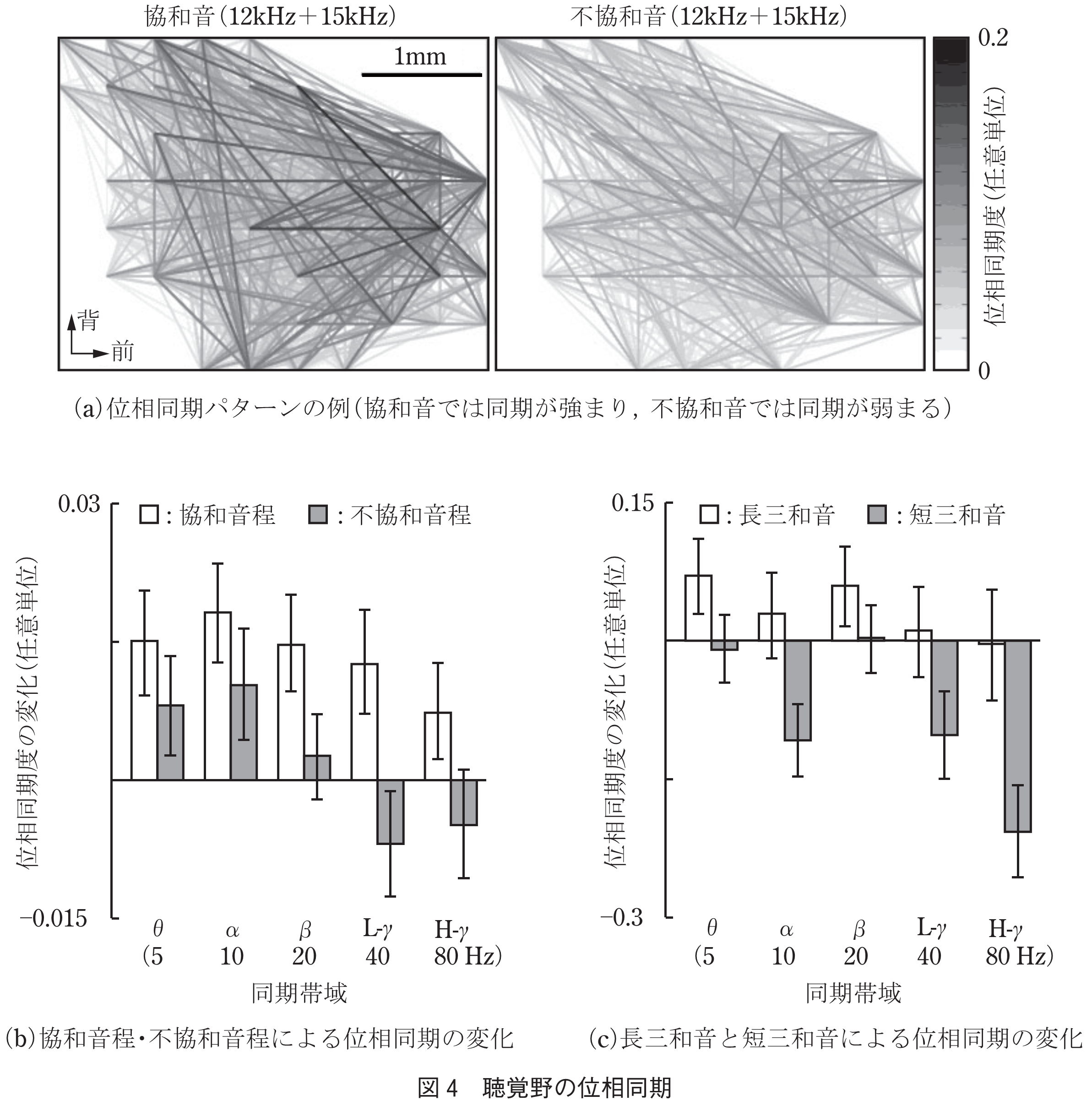
協和音と不協和音に対する聴覚野の位相同期を調べたところ,位相同期は,協和音に対しては不協和音に対してよりも,帯域にかかわらず強くなった.特に,帯域以上(>15Hz)の位相同期は,単独の構成音を提示したときと比較すると,協和音を提示した場合は強くなり,逆に不協和音では弱くなった(図4(b)).同様に,音の調性でも調べたところ,
帯域(8~14Hz)と
帯域(30~80Hz)において,長三和音は短三和音よりも位相同期を高めることが分かった(図4(c)).一般的に,高周波数成分の神経活動は,領野内の情報処理に適しており,低周波数成分の神経活動は,離れた領野で位相を同期できることから,領野間の情報伝達に適していると考えられる.音の情動的な質感が,聴覚系,情動系,高次認知系で相互に情報処理されているのであれば,これらの領野では帯域間同期が発生していると考えられる.
これらの結果から,位相同期パターンは,音の知覚に多大な影響を与えていることが示唆される.ラットが調性を知覚できるかは定かではないが,少なくとも,ラットから受け継いだ脳の同期特性が,我々が音の質感を認知する基盤となった可能性は十分にある.
本稿では筆者らの研究に基づいて,人工知能と対比しながら,脳が生み出す生命知能の原理を考察した.脳の特徴は,超複雑ネットワーク,大規模なファンイン/ファンアウト,自発活動,30周問題など,従来の計算機とは本質的に異なる.このような特徴を生かした脳の計算原理として,リザバー計算と神経ダーウィニズムが考えられる.特に脳からの知能の創発特性には,多様な活動パターンの創出とそこからの秩序の抽出が重要な要件であると考える.これらの仮説の下,神経細胞の分散培養系でリザバー計算を試み,身体化された培養神経回路が迷路課題を解決できることを示した.また,ラットの聴覚野では,周波数マップの面積が神経細胞の多様性を反映していることを示した.更に,少なくともラットから受け継いだ脳の同期特性が,音の協和性や調性といった豊かな質感認知に関わる可能性を示した.このような脳の特性は,脳に特異的な構造上の特徴から生じ,知能や芸術の創発に重要な役割を担ってきたと考える.
人工知能と生命知能を一言で対比するならば,人工知能の目的は「自動化」であり,生命知能の目的は「自律化」である.自動化のための人工知能技術は,膨大なデータを用いて事前に入念に学習し,特定の状況下で特定の問題を解くことを想定している.そのため,不完全で雑音を含むデータによる学習や,時々刻々と変化する状況(コンテクスト)へのリアルタイム処理,非同期的に得られるマルチモーダルな情報処理など,解決すべき課題も多い.これらの課題を克服するためには,生物や脳に学ぶ自律化技術が今後ますます重要となると考える.
本研究は,AMED(JP18dm0307009),NEDO(18101806-0)の委託業務,科研費(18H04999, 17K20090),立石科学技術振興財団,旭硝子財団などの支援を受けた.
(1) F. Rosenblatt, “The perceptron: A probabilistic model for information storage and organization in the brain,” Psychol. Rev., vol.65, no.6, pp.386-408, 1958.
(2) K. Fukushima, “Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position,” Biol. Cybern., vol.36, no.4, pp.93-202, 1980.
(3) J.A. Feldman and D.H. Ballard, “Connectionist models and their properties,” Cogn. Sci., vol.6, no.3, pp.205-254, 1982.
(4) J. McClelland, B. McNaughton, and R. O’Reilly, “Why there are complementary learning systems in the hippocampus and neocortex, insights from the successes and failures of connectionist models of learning and memory,” Psychol. Rev., vol.102, no.3, pp.419-457, 1995.
(5) 高橋宏知,メカ屋のための脳科学入門 脳をリバースエンジニアリングする,日刊工業新聞社,東京,2016.
(6) 高橋宏知,続・メカ屋のための脳科学入門 記憶・学習/意識編,日刊工業新聞社,東京,2017.
(7) M. Abeles, Corticonics: Neural Circuits of the Cerebral Cortex, Cambridge University Press, New York, 1991.
(8) D.E. Rumelhart, G.E. Hinton, and R.J. Williams, “Learning representations by back-propagating errors,” Nature, vol.323, no.6088, pp.533-536, 1986.
(9) M. Lukoševičius and H. Jaeger, “Reservoir computing approaches to recurrent neural network training,” Computer Science Review, vol.3, no.3, pp.127-149, 2009.
(10) “小特集 リザバーコンピューティング,”信学誌,vol.102, no.2, pp.107-149, Feb. 2019.
(11) W. Maass, T. Natschlager, and H. Markram, “Real-time computing without stable states: a new framework for neural computation based on perturbations,” Neural Comput., vol.14, no.11, pp.2531-2560, 2002.
(12) H. Jaeger and H. Haas, “Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication,” Science, vol.304, no.5667, pp.78-80, 2004.
(13) D.V. Buonomano and W. Maass, “State-dependent computations: spatiotemporal processing in cortical networks,” Nature Reviews Neuroscience, vol.10, no.2, pp.113-125, 2009.
(14) L.F.B Abbott, B. DePasquale, and R.M. Memmesheimer, “Building functional networks of spiking model neurons,” Nat. Neurosci., vol.19, no.3, pp.350-355, 2016.
(15) G. Edelman, “Neural Darwinism, selection and reentrant signaling in higher brain function,” Neuron, vol.10, no.2, pp.115-125, 1993.
(16) H. Takahashi, R. Yokota, and R. Kanzaki, “Response variance in functional maps: neural Darwinism revisited,” Plos One, vol.8, no.7, e68705, 2013.
(17) H. Takahashi, S. Yasuda, Y. Yada, and R. Kanzaki, “Reservoir computing with dissociated neuronal culture,” Frontiers in Neuroscience, Conference Abstract: MEA Meeting 2016, 2016.
(18) D.J. Bakkum, U. Frey, M. Radivojevic, T.L. Russell, J. Müller, M. Fiscella, H. Takahashi, and A. Hierlemann, “Tracking axonal action potential propagation on a high-density microelectrode array across hundreds of sites,” Nature Commun., vol.4, 2181, 2013.
(19) Y. Yada, R. Kanzaki, and H. Takahashi, “State-dependent propagation of neuronal sub-population in spontaneous synchronized bursts,” Front Syst. Neurosci., vol.10, 29, 2016.
(20) Y. Yada, T. Mita, A. Sanada, R. Yano, R. Kanzaki, D.J. Bakkum, A. Hierlemann, and H. Takahashi, “Development of neural population activity toward self-organized criticality,” Neurosci., vol.343, pp.55-65, 2017.
(21) D. Sussillo and L.F. Abbott, “Generating coherent patterns of activity from chaotic neural networks,” Neuron, vol.63, pp.544-557, 2009.
(22) T. Nakagaki, H. Yamada, and Á. Tóth, “Maze-solving by an amoeboid organism,” Nature, vol.407, no.6803, pp.470-470, 2000.
(23) S.I. Nishimura, M. Ueda, and M. Sasai, “Non-Brownian dynamics and strategy of amoeboid cell locomotion,” Phys. Rev. E, Stat. Nonlinear Soft Matter Phys., vol.85, no.4, 041909, 2012.
(24) 鹿山敦至,矢田祐一郎,高橋宏知,“神経細胞の分散培養系における集団同期発火パターンとネットワーク構造の発達,”電学論(C),vol.139, no.5, pp.570-578, 2019.
(25) 高橋宏知,“聴皮質の情報処理,”音響学誌,vol.67, no.3, pp.119-124, 2011.
(26) 高橋宏知,“聴知覚と聴覚野の神経活動の位相同期,”Audiology Japan, vol.61, no.4, pp.246-253, 2018.
(27) 白松知世,高橋宏知,“聴覚―音の質感認知,”Brain and Nerve―神経研究の進歩,vol.67, no.6, pp.679-690, 2015.
(28) T.I. Shiramatsu, T. Noda, K. Akutsu, and H. Takahashi, “Tonotopic and field-specific representation of long-lasting sustained activity in rat auditory cortex,” Frontiers in Neural Circuits, vol.10, 59, 2016.
(2019年4月13日受付 2019年5月6日最終受付)
オープンアクセス以外の記事を読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード