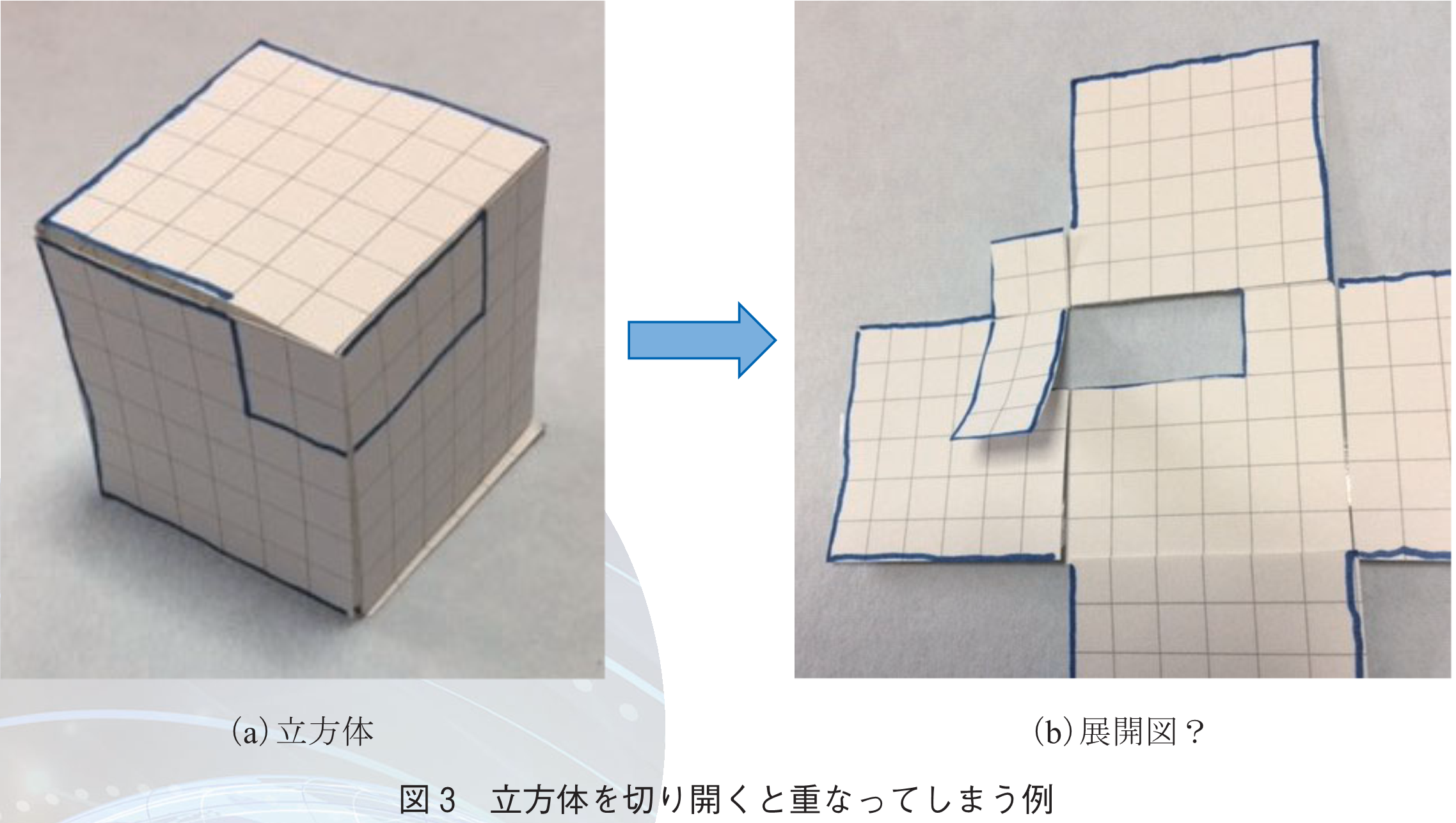
読者の皆さんは小さい頃「折り紙」を楽しんだことがあると思う．そのときは，何を折っただろうか．鶴だろうか．風船だろうか．筆者は子供の頃に風船を折って「これは『風船』じゃないんじゃなかろうか？」と思ったのをよく覚えている．風船と呼ばれる折り紙をきちんと折ると，これは風船というよりはむしろ立方体だ．この立方体をはさみで切って広げてみよう．立方体を切り開いて得られる図形を立方体の展開図と呼ぶことは小学校で習う．ではこれは何通りあるだろう．記憶力の良い読者なら，図1の11通りの展開図を習ったことを覚えているかもしれない．しかしこれは切り開くときに，立方体の辺に沿って切っている．例えば風船を図2(a)のように対角線の一部をうまく選んで切って開くとどうだろう．これも立派な立方体の展開図と呼べるのではなかろうか．今度は図3(a)のように切って開くとどうだろう．今度はなんと，図3(b)に示したように，広げたときに紙が重なってしまう．さすがにこれは展開図とは呼べないだろう．ここでいう展開図とは，立体を「うまく」切って広げたときに，ひとつながりで，重なりを持たないものと考えよう．学校で習ういわゆる「展開図」は，辺に沿って切ることしか考えないが，それはちょっと狭量だ．辺に沿って切るものは，辺展開図と呼ぼう．

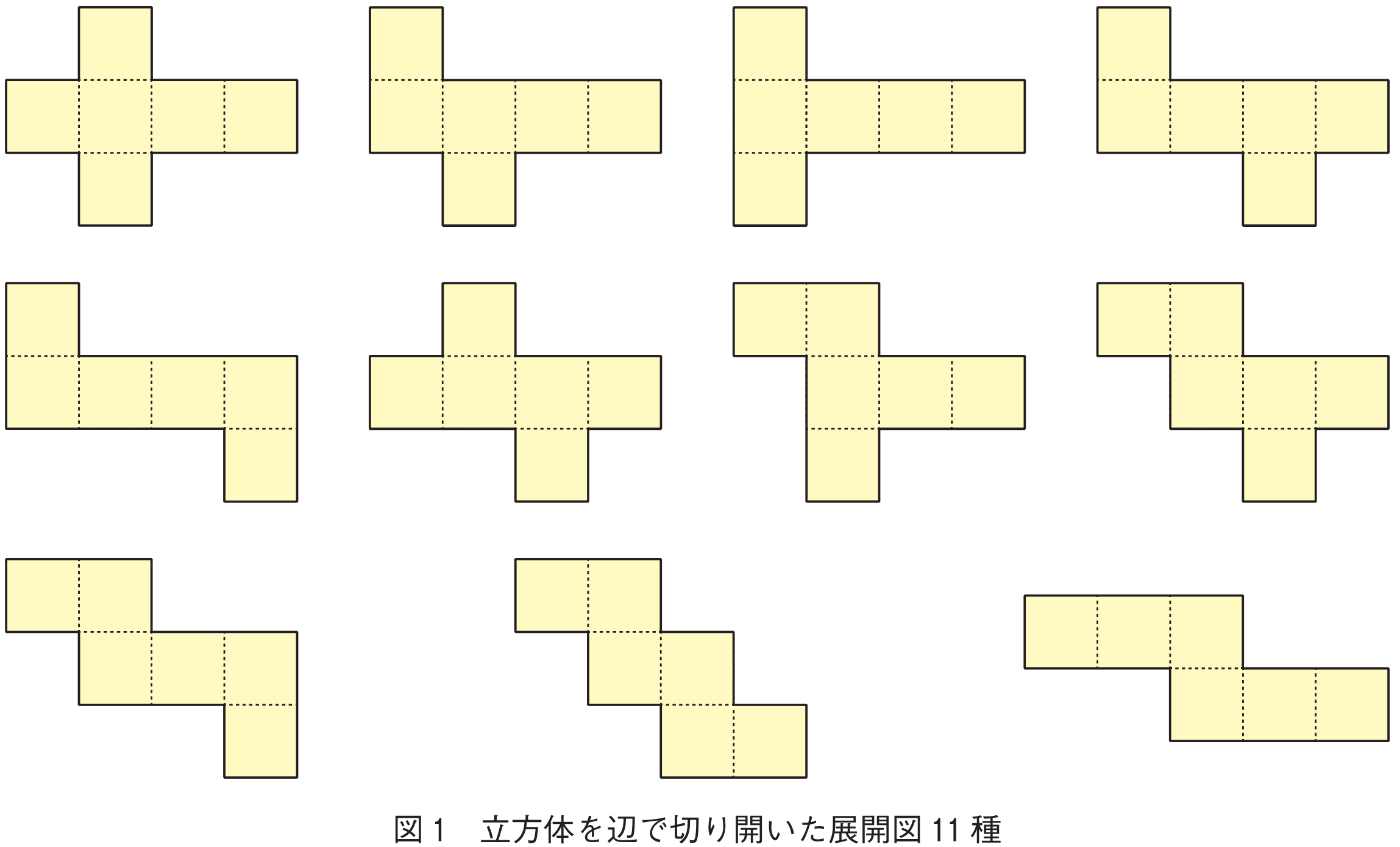
　さて，こうした平たい紙を折ったり，あるいは立体を平面に開いたりすること，つまり「折り」と「展開」は，日常ごくありふれた操作だろう．ところがこうした「折り」は，これまであまり研究の対象として取り上げられてこなかった．例えば図1の11通りの辺展開図を小学校で習った覚えのある人も，正12面体や正20面体の辺展開図を習ったことはないはずだ．それもそのはず，まず，この二つの立体はどちらも辺展開の方法がなんと4万3,380通りもある．しかも，これらを切り開いたとき，図3のような重なりが起きないかどうかは，2011年まで知られていなかったのだ．実際には，どちらの立体においても，この4万3,380通りの辺展開は重ならず，どれもきちんとした展開図になる．これは偶然だろうか？　それは今でも分からないが，幾つかの事実を考えると，正12面体や正20面体の辺展開がどれも重ならないのは，「たまたま運が良かった」だけのように見える．一方で，正12面体の辺展開の方法の個数と，正20面体の辺展開の方法の個数が同じ4万3,380通りなのは運や偶然ではなく，数学的に証明できる．

　こうした「折り」や「展開」という操作は，日常ありふれているにもかかわらず，実際にはとても難しい問題で，歴史的にも散発的にしか研究されてこなかったようだ．しかし近年，こうしたテーマは「折り紙科学」として幅広い分野で研究として認知されつつある．特にコンピュータ科学の発展に伴い，実際に計算して解析できるようになったことが大きな要因だろう．こうしたコンピュータ関連の分野を特に「計算折り紙」と呼ぶ．計算折り紙を軸に，折畳み構造や，多面体の展開の研究といった数理的な研究から，産業への応用，更には分子生物学におけるたん白質の折畳み構造や，果ては細胞に折り紙を折らせるといった，幅広い研究が今はホットな研究分野なのである．興味を持った読者には，最初の手掛かりとして本会誌2019年4月号の「小特集　折り紙の科学」⁽¹⁾をお薦めしよう．