1.1　光研究はノーベル賞の宝庫

　光科学技術は社会の基盤であり，関連するノーベル賞を毎年のように輩出している．そのため，光の性質を余すことなく利活用する技術が実現すれば，広範な分野の科学技術を画期的に進展させることができる．光の広範な性質を自在に操る技術は近年急速に進展してきているが，その対象となる性質，精度や範囲において，広大な未踏領域があり，技術開発のポテンシャルがある．

　近年，光周波数コムの技術が急速な進展を見せており，光の制御・操作技術を大きく変革しようとしている．光周波数コム（コムはくしのこと．光コムともいう．図1）は，光周波数軸上に多数のくしの歯状のモードを持つ光であるが，ここで扱い，近年様々な応用で注目されている光周波数コムは，単なるくしの歯構造を持つスペクトルを発する光ではない．それらの多数の周波数モードが精密に位相関係をもって結び付いている制御性の高い高度な光である．光周波数コムによる光周波数絶対計測技術が誕生してから20年がたち，同時に2005年のノーベル物理学賞受賞から15年を迎えたが，光周波数コム技術は，それ自体はもとより，当初予測のされていなかった分野へと展開を広げ，ますますの発展を見せている．それは，光周波数コムが，単に当初考えられていた「物差し」としての計測ツールではなく，光そのものの性質を操る「光シンセサイザ」という広範な科学技術の基盤ツールだからと言える．本稿では，光周波数コムの誕生に関わる歴史と，その光の本質と関わる科学技術における意義について述べたい．

1.2　メートルの定義と光周波数計測

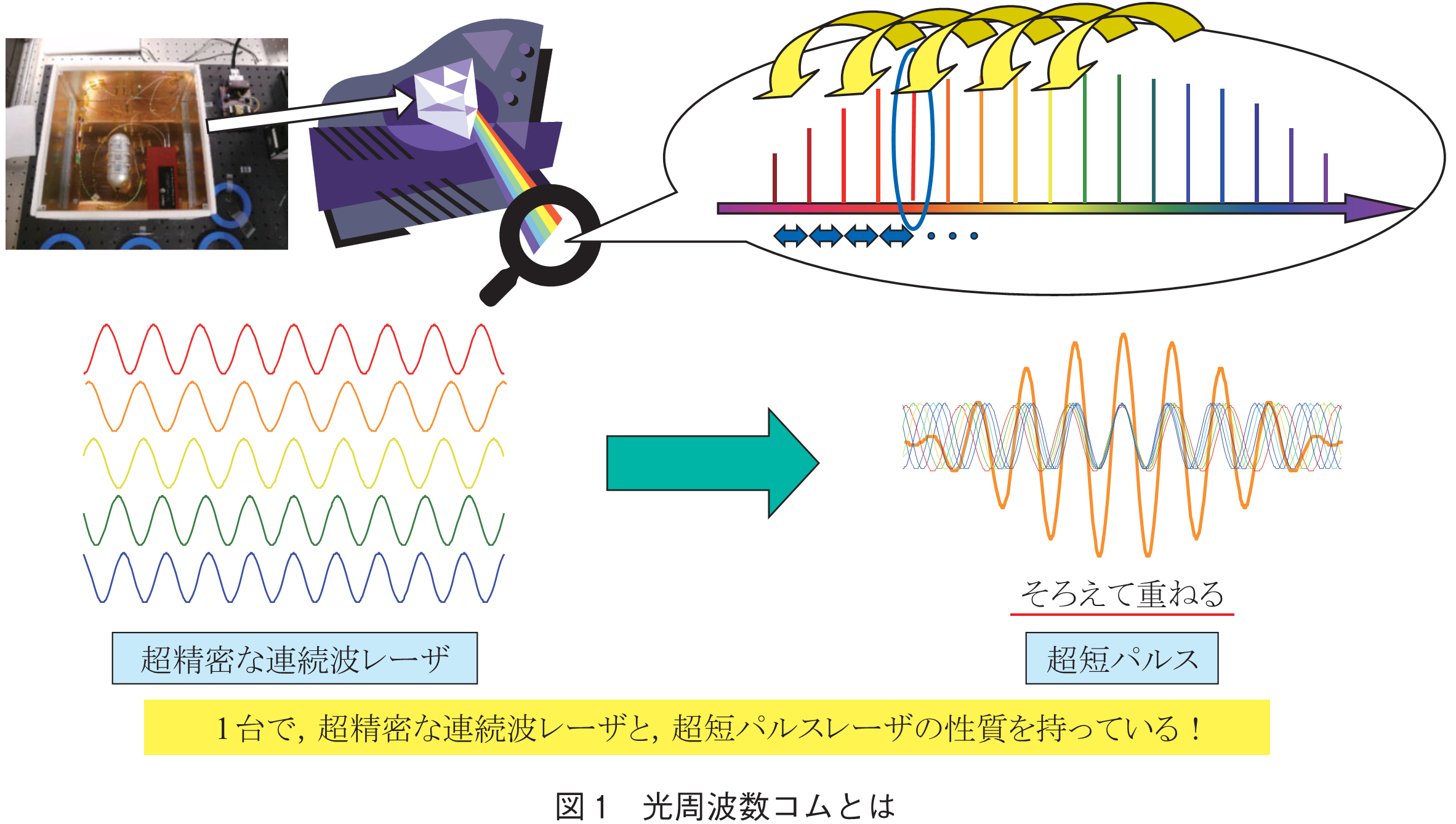
　光周波数コム技術の歴史を振り返ると，初期の研究開発のモチベーションは，光周波数の絶対測定であった．中でも，光周波数の絶対測定が強く必要とされた場面は，単位「メートル」の定義の直接実現であった．

　2019年5月20日，SI基本単位が改訂されたことは記憶に新しい⁽¹⁾．本改訂の目玉は，基本単位の定義において最後の人工物であるキログラム原器が廃止され，全ての単位の枠組みが，基礎物理定数によって決まるようになったことである．一方，本稿の主題である光周波数コムは，これにさかのぼること35年余り前の1983年に改訂された「メートル」の定義と深く関係する^(2),(3)．その改訂によって，単位「メートル」は，いち早く真空中の光速度という物理定数によって定義されるようになり，まさに光そのものが定義となった．その結果，「メートルは，1秒の299,792,458分の1の時間に光が真空中を伝わる行程の長さである」となった．これは真空中の光の速さを299,792,458m/sと定義したことと等価である．本定義は極めて高精度で安定かつ普遍的である点で優れているが，一方，単位の定義はそれ自体のみでは，実際の科学技術の現場で用いることは難しく，それを正しく「実現」する手法が同時に必要となる．そのため，このとき同時に，国際度量衡委員会は，メートルの定義を実際に実現する方法として，以下の3通りのいずれかによることを勧告した⁽⁴⁾．

 （ａ）距離の関係から，時間の測定による方法（時間測定法）；

 （ｂ）波長の関係から，レーザ周波数の絶対測定による方法（波長測定法）；

 （ｃ）勧告された周波数安定化レーザを用いる方法（放射リスト法）．

　まず，(ａ)の時間測定法は，パルスレーザを用いてその飛行時間を測定することによって距離を求めるというものである．実際にこの手法を用いて，アポロ11号をはじめとする幾つかの宇宙船が月面に残してきた反射鏡を用いて月までの距離が測定された⁽⁵⁾．この方法は，光速度に基づくメートルの定義を直接的に実現できるという点で優れている．一方，高精度な長さ計測のためには，パルスの飛行時間の高精度測定が必要となるが，当時は短パルスレーザ技術に限界があり，超短時間を切り取って，高分解能・高精度に測定することは難しかった．そのため，この手法は超長距離測定のみに有効とされた．

　そこで，精密機械産業など，実用的な長さの精密計測が必要とされる分野では，(ｂ)の波長測定法によって，連続波（CW）レーザの真空波長を基準に干渉計測で長さを測定する手法が広く用いられてきた．この手法は，メートルの単位を持つ安定化レーザの波長を目盛として長さを測定するもので，一般的な物差しの感覚に近い測定と言える．しかし，光速度の定義から光の波長を求めるには光周波数の精密な値が必要となるが，レーザの周波数を絶対測定することは困難を極める技術であった．なぜ，光周波数の絶対測定が難しかったのか．それは，一言で言えば，周波数が高過ぎて，既存のエレクトロニクス技術では直接測定ができないことが原因である．更に，光周波数の“絶対”測定という場合，それは，周波数の基準（標準）に基づいて測定することを意味するが，現在の周波数標準（秒の定義）はセシウム原子のエネルギー準位による9.2GHzの原子時計であり，例えば精密測定に良く用いられるHeNeレーザの周波数は474THzであり，5万倍かけ離れている．そのため，次善の策として，長さ測定に用いるレーザの光周波数を実際に測定するのではなく，(ｃ)の勧告された周波数安定化レーザを利用することにより，その放射リストに掲載された周波数値をいわば“信じて”用いていた．

　一方で，レーザの絶対周波数測定への努力は続けられ，幾つかの国家的プロジェクトとして取り組まれた．それは，周波数チェーンという技術で，9.2GHzのセシウム原子時計を出発点とし，各々が既に大掛かりなマイクロ波発振器やレーザを何台も用い，それらの比較によって少しずつつないでいき，数百THzの光周波数にたどり着くという大変大掛かりな実験装置であった．そのため，可視光レーザ（波長657nm，周波数456THz）の周波数測定が初めて実現されたのはメートルの定義が改定されてから10年以上がたった1996年であった⁽⁶⁾．しかし，周波数チェーンは，このように実験が大掛かりで日常的に行うことはできないもので，これをもって，長さ測定を行うことはできない．そのため，あくまで，たまに測定を行うことによって，(ｃ)の放射リストに基準を与えるというものであった．更に，このように大掛かりな測定を行っても，測定手法自体が，いわば，短い物差しをつないでいくようで，不確かさの増大を引き起こす上に，対象となるレーザが換わるごとに組合せを変えなければならず，精密測定の観点からは決して望ましい手法とは言えなかった．そこで，広範囲の周波数スパンを一気にリンクする“長くて正確な光の物差し”が切望されたのである．

1.3　｢光の物差し」の誕生

　20世紀も押し詰まった頃，時間軸上の超短パルスレーザ発生法として広く知られるモード同期レーザを，フーリエ変換で結ばれる光周波数軸上の極めて等間隔な光周波数モード列，すなわち光周波数の精密な物差し「光周波数コム」として用いる報告がなされ，瞬く間に画期的な成果が上げられていった．まず，1999年にドイツマックスプランク研究所で大きく離れた二つのレーザの周波数を一気に比較する手段として実証された⁽⁷⁾．更に，2000年にアメリカJILA研究所によって，その頃急速に進展したフォトニック結晶ファイバ技術を利用して発生された1オクターブに及ぶ超広帯域光を用いて自己参照法が実証され⁽⁸⁾，光周波数コムのくしの歯周波数の全てに絶対値が付与される革新的技術が実現された．これらによって，それまで長年の努力によってようやく実現された大掛かりな国家的プロジェクトレベルであった光周波数測定が，一人の大学院生レベルの実験となり，日常的に行える“全ての人のための技術”となった．しかも，簡易になったにもかかわらず測定精度は圧倒的に向上し，またレーザが換わるごとに構成を組み替える必要がない，汎用的な“長くて正確な光の物差し”として用いることができる．光周波数コム技術は，まさに光の世界のイノベーションをもたらす技術であった．その登場以来急速に進展し，20世紀中，すなわちその誕生から1～2年のうちに，前述のドイツ，アメリカに加えて日本^(7)～(9)の3か国において，相次いで光周波数の絶対計測実現に至った．

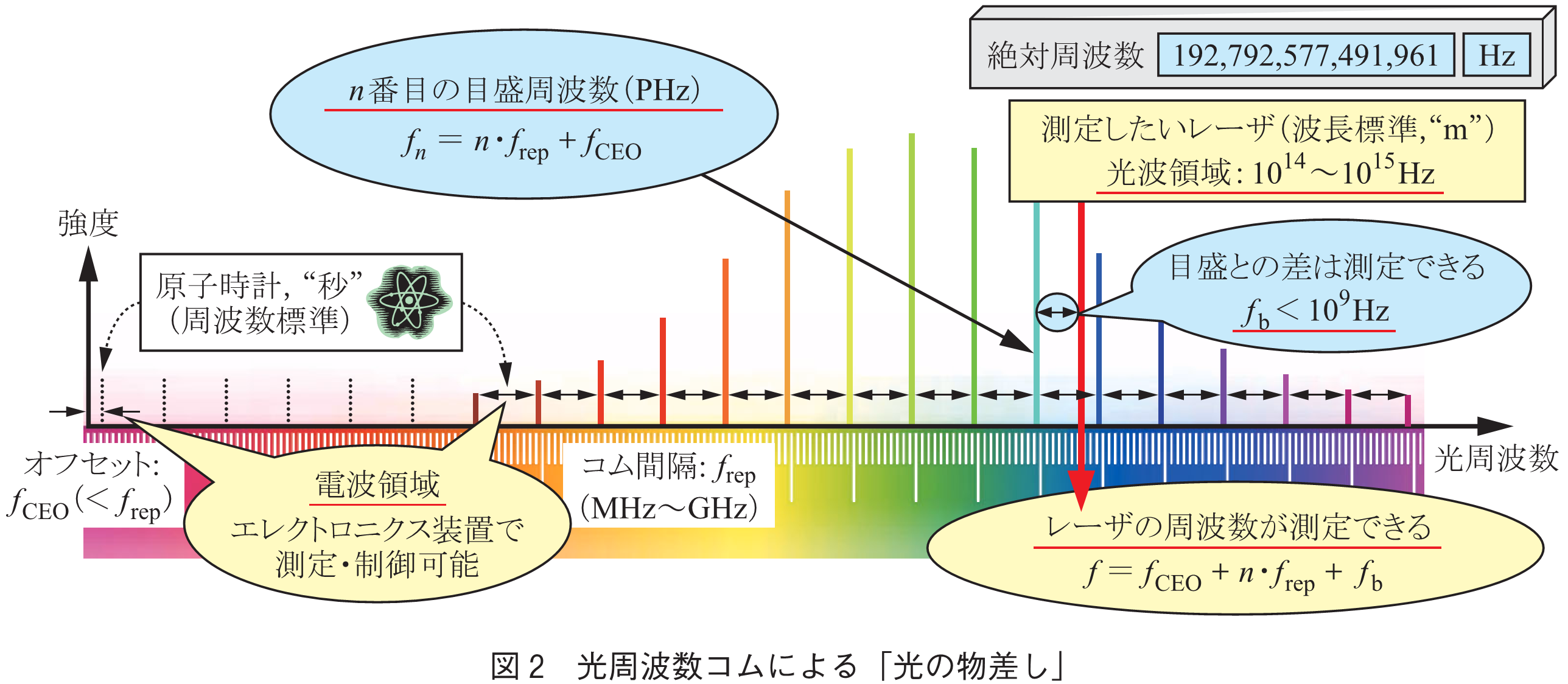
　光周波数コムの真髄は，構成するくしの歯に相当する多数の光周波数モードが極めて高精度に等間隔を保って存在することにある．そのため，図2に示すように，番目のモードの光周波数をと書くと，のように，繰返し周波数（コム間隔）と，オフセット周波数（キャリヤエンベロープオフセット周波数）という，たった二つのパラメータを用いた一次式で全てが記述できる．すなわち，この二つの周波数パラメータを測定・制御することにより，数百THzの値を持つ光周波数が広範囲にわたり高精度に測定・制御できることを意味する．特に，広く用いられる光周波数コム光源においては，，はマイクロ波帯などの既存のエレクトロニクス装置で測定できる領域にあるため，任意のレーザの光周波数が，光周波数コムのモードとビート測定するだけで，既存のエレクトロニクス装置で高精度に絶対測定できることになる．これが，「光の物差し」（「光周波数の物差し」）と呼ばれるゆえんである．

　光周波数コム技術は，このように，周波数計測の分野に革命をもたらした．そして，誕生から約5年にして2005年のノーベル物理学賞受賞に至り⁽¹⁰⁾，それを契機にますます進展が加速しており，現在に至ってもその勢いは衰えていない．日本は，前述のように，その初期から光周波数コム技術の進展に大きな貢献をしてきており，2009年には長さ分野の特定標準器として確立するに至った．これらの，「光周波数の物差し」としての光周波数コムの意義を総括すると，広範な周波数帯をコヒーレントにリンクすることができるということに尽きる．それは，大きくかけ離れた電波と光波の領域をつなぎ，同時に，秒の定義（周波数標準）とメートルの定義（長さ標準）をつなぐものである．現在，全ての物理量の中で最も精密に定義されているものは「周波数」であるから，このことは，長さ標準（波長標準）にも高精度と広範囲を同時にもたらすものといえ，広範な科学技術や産業において大きな意義がある．同時に，逆に精密さで上回る光周波数を基準として秒を定義する光格子時計⁽¹¹⁾に代表される光時計の実現など，周波数計測・標準の分野を一変する動きが次々と起こっている．近年，次の単位系の大きな改訂として議論されている「秒」の定義においても，高精度な光時計の比較手段として必須の役割を担っている．このように，光周波数コムは人類が手にした最も精密な物差し，「光の物差し」であり，2005年のノーベル物理学賞は，その意義が認められたものといえる．

1.4　光周波数コムと超短パルス

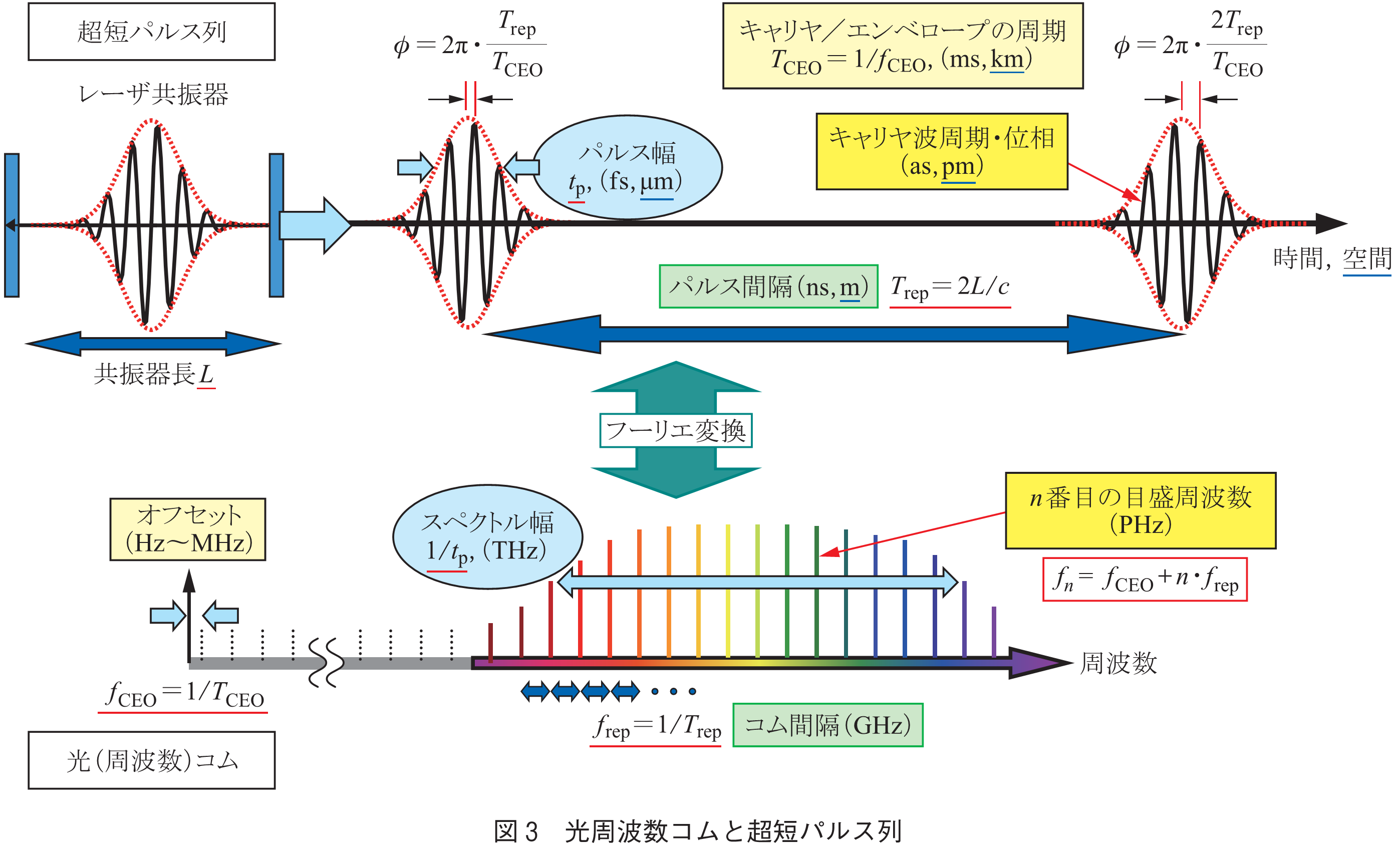
　ここで光周波数コム技術の誕生の歴史に視点を戻すと，モード同期レーザが多数の光周波数モードを形成することは数学的にはフーリエ変換の関係として自明なことだが（図3），実際のモード同期レーザにおいて，精密計測に利用価値のある高精度なモード列を得ることは容易ではなかった．そのため，科学技術分野としては，長らく，連続波レーザによる光周波数計測と，超短パルスレーザ分野は全く無縁な発展を続けてきていたと言ってよい．上述した光周波数計測技術の進展の一方で，超短パルスレーザ分野においては，独立に，より短く安定なパルスを発生させるための努力が続けられてきており，20世紀の終わりには，フェムト秒パルスが安定に制御性良く発生できるようになってきていた．その超短パルスレーザ発生・制御技術の進展が，結果的に光周波数コム技術を爆発的に進展させたのである．すなわち，時間軸上で安定な超短パルスを発生させるための技術的努力は，同時に光周波数コムとしても優秀な光を発生させることにほかならなかった．光周波数コムの登場によって，超短パルスレーザと超精密な連続波レーザという，相反すると思われていた性質を併せ持つ光源技術が誕生し，時間軸の超高速と周波数軸の超精密という，従来直交して進展してきた技術分野同士が究極において融合するドラマチックな出来事が起きたのであった．

　このように光周波数コムは，異分野融合の側面を本質的に有するからこそ，単に周波数計測分野に恩恵をもたらしただけでなく，広範な科学技術分野に進展をもたらし続けていると言える．それを端的に表す例として，本稿の最初に述べた単位「メートル」の定義の実現技術，すなわち長さ計測技術について触れておきたい．前述のように，当初，「波長測定法」に必要な光周波数の絶対測定手法を追い求めることから生まれた光周波数コム技術であったが，結果的に，独立に進展してきた超短パルスレーザによる「時間測定法」と融合し，大きな変革をもたらした．すなわち，光周波数コムを単なる連続波レーザの波長校正のためのものさしでなく，直接的に「長さ測定光源」として用いた「光周波数コム長さ計測」という新分野となって，脚光が当たることになった．まず，光周波数コムによる周波数測定技術の初の実現と時を同じくして，1999年には世界で初めて光周波数コムを測定用光源として用いた長さ測定「コム距離計技術」が筆者らによって実現された^(12)～(14)．これは，光周波数コムのモード間ビートの位相測定による，光の飛行時間測定に基づく距離測定であった．この研究を契機として，光周波数コムを光源とした様々な干渉計測やライダなどの手法に基づいて，原子サイズから宇宙レベルまでの広範な精密距離測定技術の研究が，現在に至るまで世界各地で盛んに行われている^(15)～(17)．

1.5　｢周波数物差し」を超えて発展

　このように，光周波数コムのポテンシャルは，単なる「光周波数の物差し」にとどまらない．実際，光周波数コムの応用は，前述の「光周波数コム長さ計測」をはじめとして，当初の予想をはるかに超えて拡大し続けており，現在も多くの未開拓分野で期待されている．「周波数」は，全物理量の中で最も精密で大きなダイナミックレンジを持ち，かつ成熟したエレクトロニクスの装置や手法によって扱うことができる．光周波数コムは，電波と光という単なる周波数リンクのツールではなく，光とエレクトロニクス技術の垣根を取り払い，「異なる科学技術分野同士のコヒーレントなリンク」を実現するツールといえる．これにより，光波の位相レベルの制御技術が革命的に進展し，従来実現できなかったレベルの精密さに加え，圧倒的なダイナミックレンジが利用できるようになってきた．

　まず，圧倒的な高精度性を持つ光周波数コムを，異なる物理量同士の変換ツールとして用いることによって，ある分野で発展してきた技術を他分野でも高精度に取り入れることができ，これまで別々に進展してきた分野の技術同士が相互に乗り入れることができる．例えば，光による干渉計測やセンシング，イメージング技術において，エレクトロニクス分野の成熟した技術，例えばヘテロダイン，ビート検出，周波数計測や制御，信号処理を駆使して，自在な処理や高精度性，広帯域性を導入することができる．まさに，光を電気のように自在に使うことができるということである．更に，光周波数コムによって精度に圧倒的な余裕のある周波数計測に基づいて，他の物理量を扱えるようになったことは，単に高精度測定が可能になるということにとどまらない．光周波数コムの応用について語るとき，その応用においてそれほどの高精度を必要としていないという議論がしばしば聞かれるが，それはポテンシャルを十分活用できていないということにほかならない．その精度の余裕を活用することで，例えば，従来は精度や範囲と速度のトレードオフによって実現できなかったリアルタイム性を付与したり，精度を犠牲にすることなく新たな制御性を導入するなどの高機能性を実現できることになる⁽¹⁸⁾．このような活用法は，今後，更に発展が期待できる．

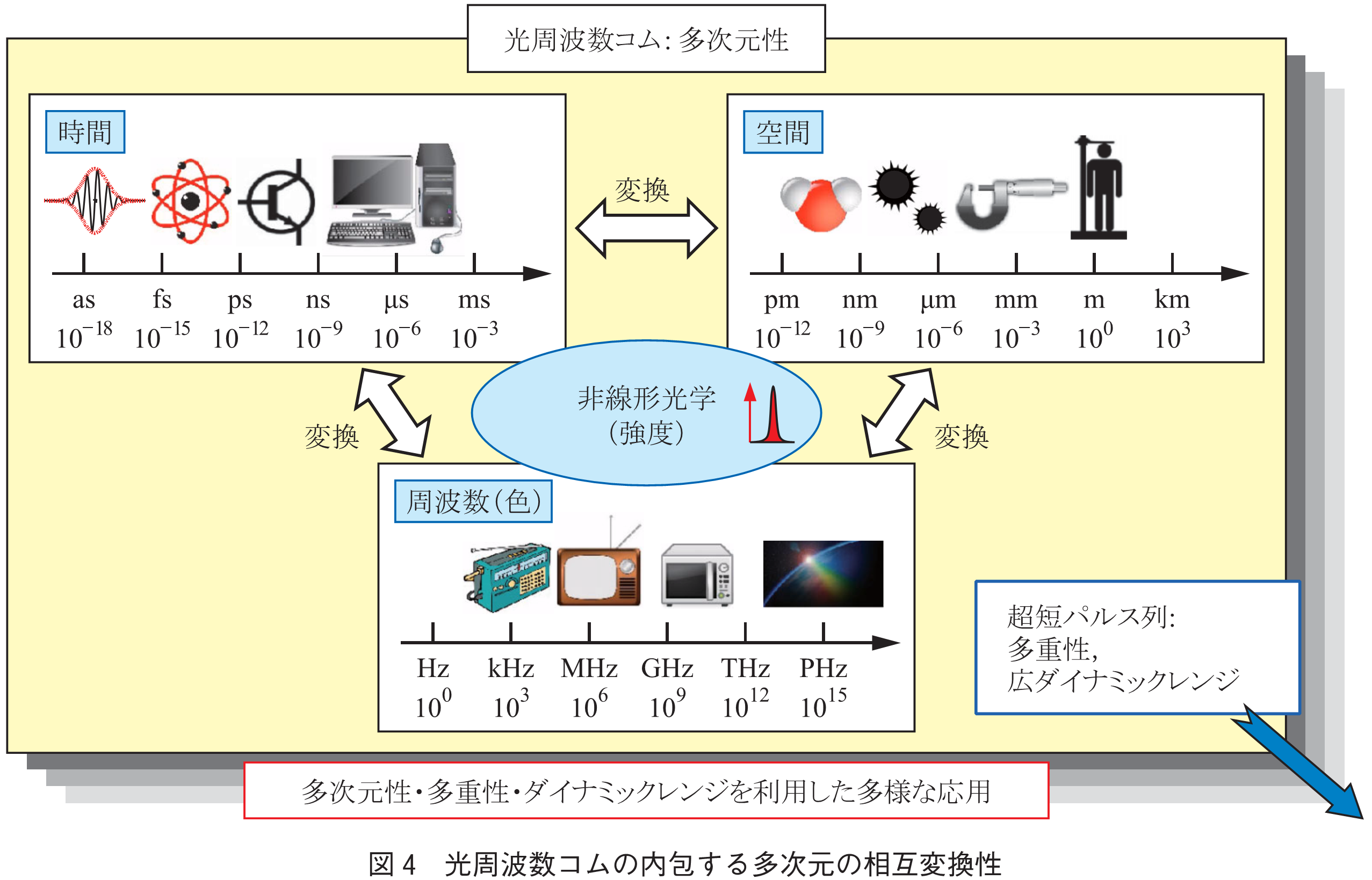
　次に，周波数軸上の光周波数コムは，フーリエ変換の関係で時間軸上の超短パルス列と精密に結び付く（図3）．周波数軸上で，HzからPHzまでの広範囲にわたり，お互いにコヒーレントにリンクしている精密な多数の基準を有する性質は，時間軸上においては，アト秒からミリ秒レベルの広範囲に対応する．例えば，標準的なモード同期レーザによる光周波数コムの場合は，10ナノ秒間隔で正確に出力される100フェムト秒の包絡線を持つ超短パルス列の利用と同時に，パルスの包絡線に内包されるキャリヤ波の位相を用いることでアト秒時間軸が利用できる．更に，キャリヤに対するエンベロープの周期は設定によってミリ秒以上の長期の正確な時間軸基準を与えるため，アト秒からミリ秒以上の時間軸をシームレスに扱えることになる．同時に，これを光の伝搬する空間距離に換算すると，ピコメートルからキロメートルの範囲に相当する．このように，光周波数コムの多次元性によって，空間・時間・周波数の多次元物理量の間で相互に変換可能で，しかも，各々が高精度かつ制御性を持った多重レンジの基準を用いることができる．つまり，これらのどれかの性質を測定したり，制御しようと思ったときに，必ずしもそれ自体を用いる必要はなく，極限的な精密性を失わずに別の都合の良い量，例えば良い検出手段のある量を代わりに用いることができる．このような次元変換の性質を利用すると従来技術の制限要因を回避した多彩な応用が可能となる（図4）．そして，光周波数コムの多次元性は，これらの軸にとどまらず，強度，偏光，横モード，角度などの広範な物理量に拡張可能であり，実際にその可能性が示され始めている．すなわち，光周波数コムは，単なる物差しでなく，光を自由自在に制御・操作するツール「光シンセサイザ」である．これは，音の世界のシンセサイザが音楽を自由に奏でられるのに似て，光周波数コムは光の楽器であり，究極の夢のツールである⁽¹⁹⁾．

　以上のような光周波数コムの魅力的な性質を用いると，材料，環境，医療，イメージング，防災，産業，宇宙，天文など広範な分野において，多くの革新的な応用が開かれると期待される．実際，ノーベル賞当時の「光周波数の物差し」からは想像できなかった広範な応用がこの15年ほどで次々と誕生し，現在も拡大を続けている．

1.6　更なる未踏のポテンシャルへ

　しかし，そのポテンシャルは，特に実用的な場面でまだ十分利用されているとは言えない状況である．その理由の一つが，“光周波数コム技術の敷居の高さ”にあると言える．まず，光周波数コム光源自体が，発生そのものに加えて高周波エレクトロニクスなどを駆使した高精度な制御を要し，使いこなすのに高度な技術を要することが挙げられる．市販品も増えつつあるものの，価格やサイズ面，利便性において課題がある．加えて，光周波数コムを実際に応用しようとしたときに，例えば光の出力パワー，波長，パルス幅，繰返し周波数といった光源のパラメータが分かっただけでは使いこなすことができないことも大きな要因である．それは，光周波数コム光源自体が，従来の超精密レーザと超短パルスレーザという各々直交して発展してきた極限的分野の性質に加え，それらの融合的性質を持つためである．特に，多数のモードが同時に使えるということは，逆に使いこなすために，適した手法やノウハウが必要であることを意味する．例えば，各周波数モードの精密性を生かしたコム分光に期待が高まっているが，各モードを分解して検出するためにはコム間隔が広いことが求められる．一方で，データのサンプリング点が離散的になり過ぎては，モード分解分光の利点が生かし切れない．それに対しては，2台の光周波数コムを用いてマルチヘテロダイン検出するデュアルコム分光法^(20)～(22)など，光周波数コムならではの利用技術が発展してきている．また，光周波数コムの時間的性質を計測手段として用いた場合，超短パルスとして時間軸上に局在しており一瞬の時間を切り取れる点は応用上の大きな魅力であるが，逆にパルス間にデッドゾーンが生じることになり，計測範囲に制限が生じる．その解決には，光周波数コムが高精度に等間隔性を保つ性質（アダプティブ性）を活用することにより，高精度性を保ちながらコム間隔を走査することによって，その領域を高精度に埋め尽くす技術が必要となる⁽²³⁾．すなわち，光周波数コム技術というのは，単なる光源発生技術ではない．そのリアルな活用のためには，光周波数コムならではの独自領域の利活用技術，「光シンセサイザ技術」を必要とする．すなわち，一つの技術分野として見た場合，光源技術と応用技術の間には，もう一つの科学技術レイヤが必要となる．光周波数コムのポテンシャルを真に生かした応用のためには，それらの光源・利活用・応用基礎技術までを一体とした科学技術プラットホームの構築が必要である．それを，筆者らは，「知的光シンセサイザ」と呼び，その新たな科学技術プラットホームの存在を示す研究開発を行ってきているが，近年，多彩な分野への展開可能性が示されてきた（図5）．

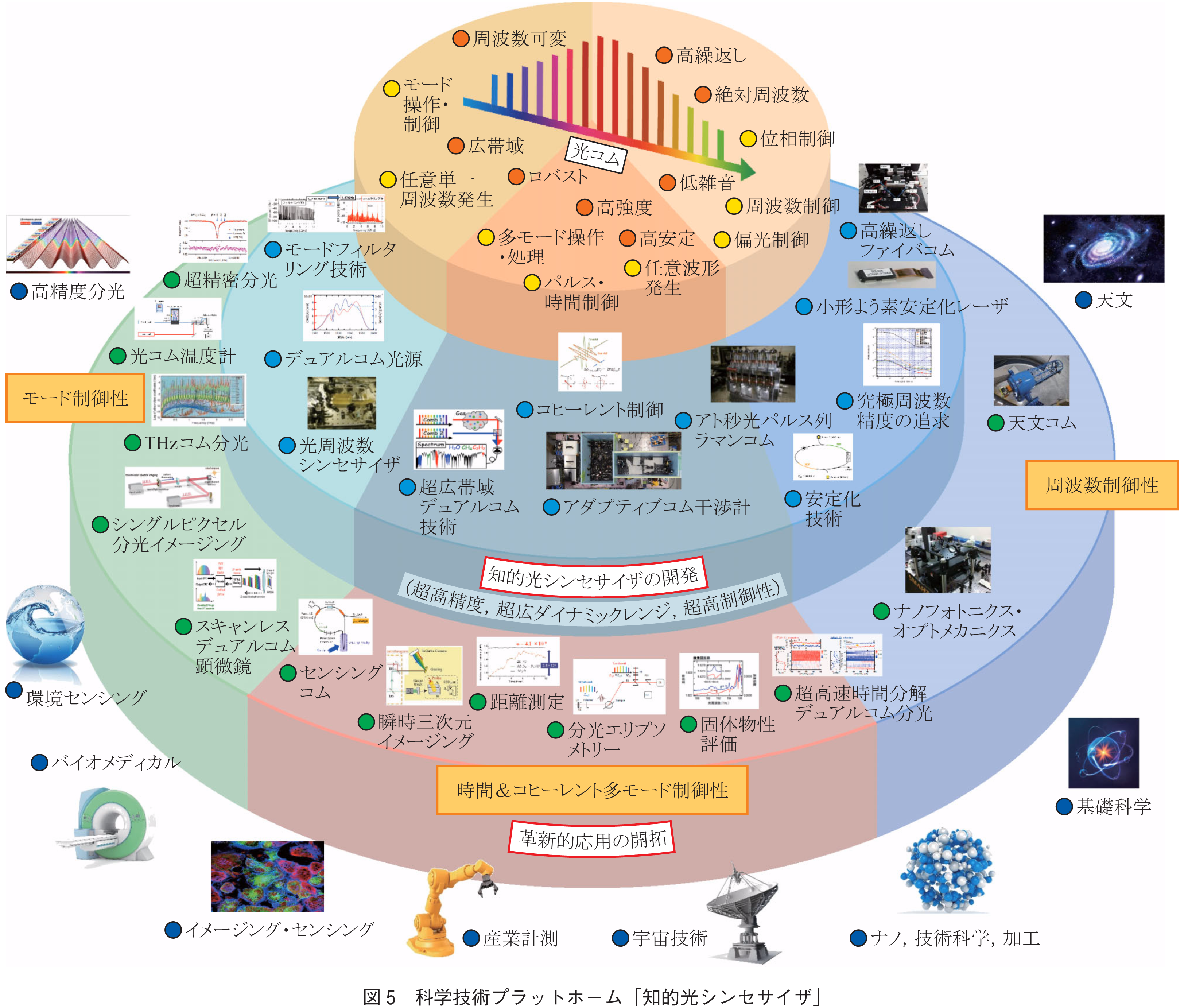
　このように，レーザのれい明期に似て，大きなポテンシャルを指摘されながら，長らく敷居の高かった光周波数コム技術であるが，近年，その様相が大きく変わり始めている．まず，光源発生技術においても，EUVからTHzやマイクロ波領域に至る広範囲の波長域での実現^(24),(25)，超広帯域発生，低繰返しから高繰返しに至る広範囲のくしの歯間隔での精密なコムの実現，超低雑音化などが示され，悪環境で使えるファイバレーザ⁽²⁶⁾や，市販もされている変調器ベース⁽²⁷⁾の光源システム，複数のコムを一体で発生させ圧倒的に簡易化するデュアルコム光源^(28)～(30)，マイクロコムなどのチップ化可能な光源とシステム化技術の進展⁽³¹⁾など，実用的技術が進展し，応用の拡大に必要な条件が急速に整いつつある．それらと並行して「光シンセサイザ技術」においても，光周波数コム同士の高精度同期，デュアルコム分光法の進展と応用拡大，モードフィルタリング法による間隔の自在選択，光周波数コムのアダプティブ性を用いた耐環境自動制御^(18),(32)，光周波数コム同士のコヒーレンス合成⁽³³⁾，空間モード制御への発展⁽³⁴⁾など，周波数のみならずコヒーレントな多モード及び時間軸・空間軸制御手法が画期的に進展している．同時に，それらを活用した応用基礎技術においても，天文⁽³⁵⁾，距離計測⁽¹³⁾，産業・バイオ・イメージング^(36)～(38)，生体・環境センシング⁽³⁹⁾，材料科学やデバイス評価^(40)～(42)など，実際に広い分野の可能性が示されつつある．

2.1　周波数物差し：周波数制御性の利用

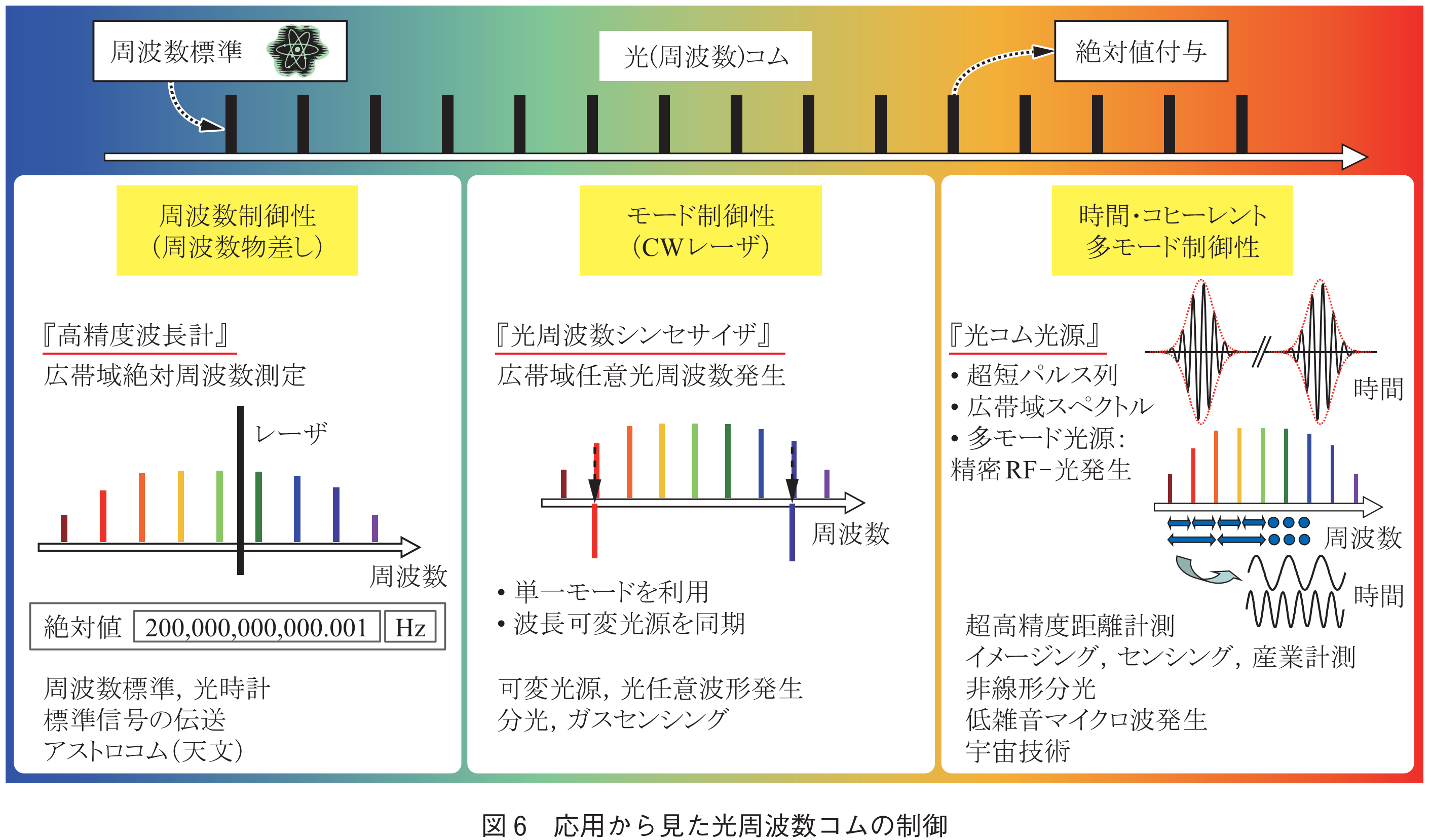
　周波数絶対値を付与された光周波数コムを「光の物差し」，すなわち広帯域かつ高精度な波長計として利用するもの．光周波数コムの利用法としては初期段階からその重要性が認識され，長さの国家標準の確立，周波数標準や光時計の進展，標準信号の伝送・配布，物理定数の評価などに強力な役割を果たして来た．近年では，更なる高精度化，低雑音化，波長帯域の拡大，高繰返し化が進み，科学技術基盤としての重要性を増している．同時に，周波数計測に基づいた新たな応用分野も広がっている．その代表例がアストロコム⁽³⁵⁾と呼ばれる天文分野への応用である．天体観測用の高分散分光器の波長校正によって装置の性能を引き出し，天体の視線速度の長期にわたる高精度測定を可能にすることで，系外惑星の探索や観測的宇宙論への寄与が期待されている．

2.2　CW光源：モード制御性の利用

　光周波数コムを単なる基準（物差し）ではなく，高精度な光源として利用する応用が広がっている．光周波数コムの各モードは，それ自体が，超精密な連続波レーザであり，一台のレーザから広帯域にわたり高精度な任意光周波数を多数発生させることができるのは，大きな魅力である．そのような利用は，マイクロ波の任意周波数発生器である周波数シンセサイザのアナロジーで，「光周波数シンセサイザ」と呼ばれる．モード間隔が10GHz程度以上の高繰返しな光周波数コムでは，単一モードを光フィルタ等で直接抜き出して利用することも可能である．そのような高繰返しコムとしては，モード同期レーザ⁽⁴⁴⁾のほかに，変調器型のコム発生器⁽²⁷⁾，非線形光学を利用したラマンコム⁽⁴⁵⁾や，マイクロ共振器によるマイクロコム⁽³¹⁾が知られており，急速に進展しているが，現状では直接発生や絶対周波数制御が困難，出力パワーや波長域が限定されるなど実用性が限定されている．一方，広く利用されているモード同期レーザによる光周波数コムは繰返し周波数が100MHz程度であり，単一モードを直接切り出すことは困難な上，切り出した場合でもモード当りの強度が弱く，応用には限界がある．そこで，波長可変CW光源を各モードに同期させることにより，光周波数コムの高精度を保ったまま，高強度かつ広帯域可変の単一モード出力を得る手法がとられる⁽⁴⁶⁾．連続波レーザから変調器を用いてサイドバンドを発生させて波長走査する場合に比べ，光周波数コムに同期することで，走査の範囲拡大と高精度化の両立が可能となり，光やTHz波領域⁽⁴⁷⁾での分光やセンシングが実現されている．また，波長走査干渉計に利用して大幅な変位量の拡大と高分解能の両立を実現し，大気中でピコメートル精度を持つ変位計測に成功している⁽¹⁶⁾．

2.3　コム光源：時間・コヒーレント多モード制御性の利用

　光周波数コムの光源としての特徴をフルに生かした利用であり，近年盛んになってきている．更に，（１）制御された超短パルス列光源，（２）広帯域スペクトル光源，（３）コヒーレント多モード光源，としての利用に分けられる．

 （１）光周波数コム全体をパルス光源として利用

　光周波数コムが高精度に制御された超短パルス列であることを利用する．超短パルスとしての超高速時間性と，パルス間のコヒーレント制御性を生かした利用が可能となる．周波数の制御により，パルスの時間軸の性質を高精度に制御することが可能で，超高速分野における位相制御という革新的ツールを与え，アト秒に及ぶ超短パルス発生と利用技術の進展に寄与した⁽⁴⁸⁾．同時に，超短パルス間のコヒーレント制御を利用した分光や計測への新たな応用の可能性も広がってきている^(33),(34)．

　このような時間軸の応用においては，超広ダイナミックレンジの時間軸を扱えることは従来にないインパクトを与える．光周波数コムを干渉計測に用いると，パルスの包絡線に局在したキャリヤ波による干渉じまが観測されるが，白色光源による低コヒーレンス干渉とは異なり，パルス列内の異なるパルスが相互に干渉する（パルス間干渉）⁽⁴⁹⁾ため，真のコヒーレンス長は各モードの線幅で決まり極めて長い．制御された光周波数コムでは，1Hz級のモード線幅が実現できる．これにより，低コヒーレンス干渉と連続波レーザによる干渉の利点を両立できる．これを距離測定に用いれば，広範囲の任意距離の高精度な絶対距離測定を実現できる．加えて，光周波数コムの周波数パラメータで実効的な光路長を可変・制御できるため，機械的ステージ走査が不要となり，高速かつ高精度な計測が可能という大きな利点がある^(23),(50)．高精度長距離計測⁽¹⁸⁾や，イメージング⁽³⁶⁾などに応用が拡大している．

 （２）光周波数コムを広帯域光源として利用

　モード同期レーザ自体が広帯域スペクトルを持つが，更に，超短パルスの高強度性を生かしてコンティニュウム発生や波長変換などの高効率な非線形光学効果により超広帯域光が利用できる．更に，広帯域スペクトルを分光検出する場合，スペクトル分解能がモード間隔より高分解能になると，装置分解能ではなく，一気に各モードの狭線幅で決まる超高分解能を実現できる．また，広帯域のスペクトル成分や多数のモードを情報キャリヤとみなして同時に情報を乗せることにより，高速性，並列性を生かした多点同時計測や大容量情報処理応用が可能となる^(38),(51)．

 （３）光周波数コムのモード間干渉（モード間ビート）を利用

　同一コム内の多数のモード同士のセルフビート，及び，複数のコム間のクロスビートを利用できる．RF，マイクロ波，THzから光周波数までの非常に広帯域な高純度の合成波長の生成とみなせ，これらの領域の電磁波を実際に発生させることが可能である．また，広帯域・高精度な変調，ヘテロダイン，ビートダウン手法として用いれば，光周波数と電気・マイクロ波周波数の変換を用いた信号処理・計測が可能である．高純度なセルフビートによる高精度な高周波変調を用いた絶対長距離計測は，光周波数コムの最初の応用例として知られる⁽¹³⁾．また，近年では，同様の手法を用いた低雑音のマイクロ波発生がセンシング応用として注目されてきている．更に，繰返し周波数の僅かに異なる二つの光周波数コムのクロスヘテロダインビートを用いて，光周波数領域の情報をRF領域にビートダウンし，多数のモード分解したスペクトル情報を同時に取得するデュアルコム法が盛んになってきている^(20)～(22)．これにより，100THz以上に及ぶ広帯域を一度にカバーして，各光周波数モードを分解できる高分解能と周波数絶対値を持ち，吸収と位相の複素光学スペクトルを，ミリ秒程度の高速かつ高感度に取得できるようになり，光周波数コムの応用性が大きく高まった．デュアルコム法は，広帯域かつ精密なガス分光のほか^(20),(52)，リモートセンシング⁽⁵³⁾，非線形分光^(54),(55)，超高速分光⁽⁴²⁾，コヒーレント制御⁽³³⁾，固体物性^(40),(41)，距離計測⁽⁵⁶⁾やイメージングなどの応用手段として注目されている．