
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|
学生/教養のページ
スミスチャートの歩き方[Ⅰ]
──LC編──
Arcs of Supreme Elegance [Ⅰ]: Lumped Constants Are Go
この上なく美しい円弧群にエレガンスを感じながらも使い方がよく分からずスミスチャートひいては高周波工学を敬遠してしまう学生君を見掛ける.その要因は何だろうか.一つにはこのチャートに複数の座標系が入り組んでおり場面に応じてそれらを間違えずに使い分ける煩わしさである.逆に言うと目的が明確であればそれに特化した簡明な読み方ができるはず.本稿では学部生が親しみ深い直並列LC回路を例にチャート上をそぞろ歩いてみる.
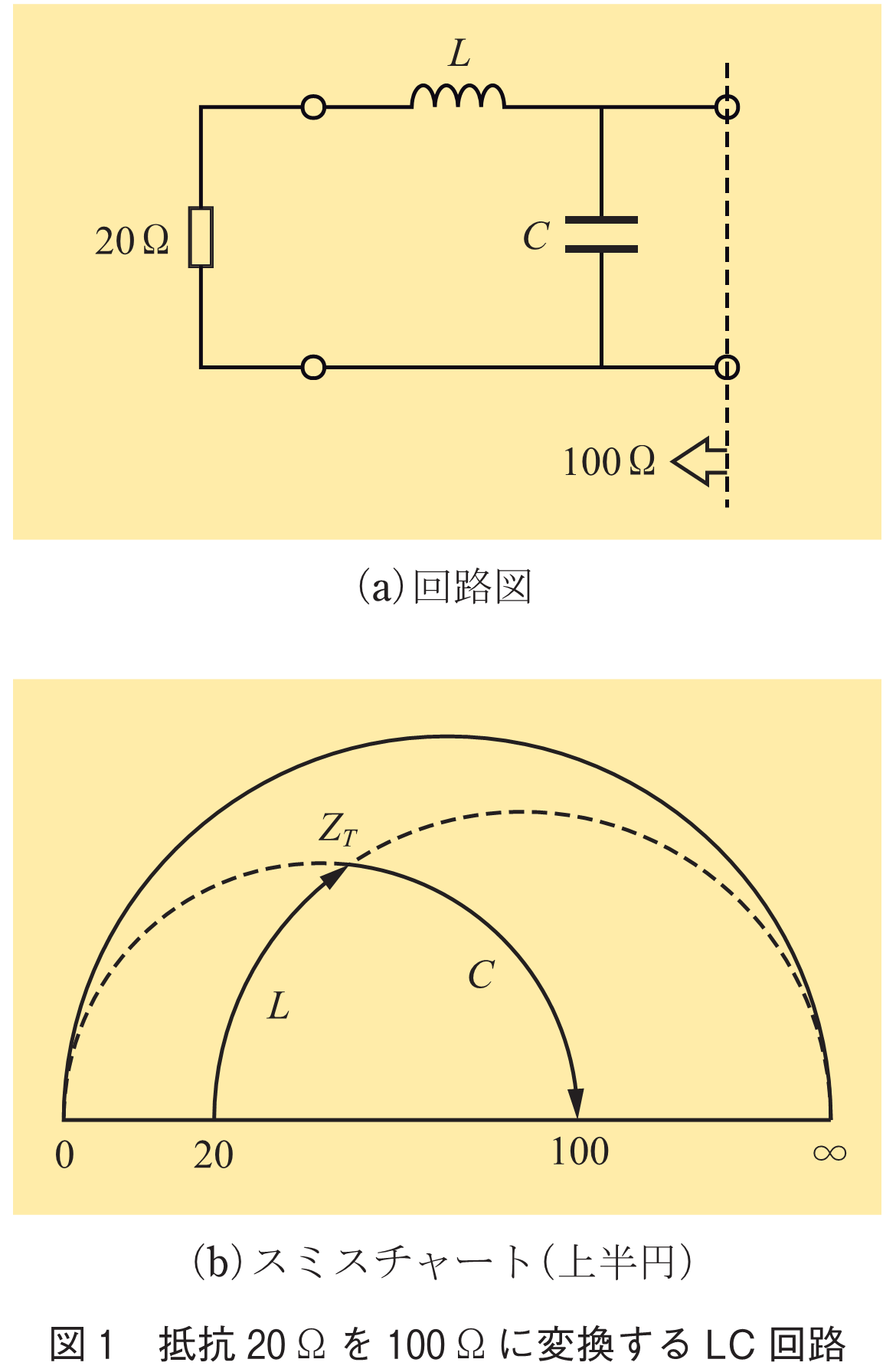
チャート上を歩く物理的意味は電気回路のイミタンス変換である.超入門の例を図1に示す.目指すは20を100
に変換するLC回路の設計.地平線上の20
から出発.コイル
を直列に付加することで右端が
に接する円(定
円)に沿って時計方向に歩く.歩いた先のイミタンスを
と書くと
(1)
である.そこからコンデンサを並列に付加することで左端が
に接する円(定
円)に沿って時計方向に歩く.その到着点が同じ地平線上にある100
なので
(2)
である.式(1),(2)からを消去する.その式を実部と虚部に分離する.それらを連立して解く.その結果
(3)
を得る.これで所望周波数に応じてLC値が決まる.超入門回路設計完了!
実用システムはもっと複雑な回路となる.そこでチャート散策に必携のアイテムを与える.交流回路の授業で学んだイミタンスの基本式
(4)
を思い出そう.これらを連立させて,
,
を消去すると
(5)
という何とも麗しき関係が導ける.これを「積」と呼ぶ.
と
が実数ゆえ右辺は全項非負.そして分子が分母を超えることはない.つまり
(6)
である.特にはチャートの外周円,
は地平線を意味する.
旅立ちの前にもう一つ強力なアイテムを授ける.再び学部の授業を思い出そう.LC素子の良さを示す指標
(7)
を習ったはず.これを式(5)に代入しについて解くと
(8)
を得る.これが積による
ファクタ公式である.
積と
の対応関係を表1に示す.この公式と早見表は次々節の演習で威力を発揮する.
目的地へ達する経路が複数存在するとどの道を選ぶか迷う.日常生活では通勤通学などあえて遠回りして歩くことが健康にプラスだろう.回路設計では素直に考えて短い経路を選ぶことが優位である.なぜならこれにより少なくとも三つのいいね:
回路内の電力損と発熱が小
回路内素子にかかる電圧電流ストレスが小
素子値の誤差や変動に回路特性がロバスト
が期待できるからだ.これらはkW級以上のRFパワエレ分野で特に有用となる.
経路の長さを測るにはどうすればよいだろうか.チャートに刻まれたイミタンス目盛では直読できない.正しく知るには非ユークリッド幾何が必要である(1).ここでは道の長さを「ポアンカレ長」と呼ぶ.記号
(ラムダ)は長さを意味するギリシャ文字…何だか雲行きが難解になってきた.でもそこで心折れてはいけない.君には二つの強力なアイテムがある.これを使えば
がエレガントに求まるのだ.その手法を基本例で習得しよう.
一般に滑らかな曲線の長さを求めるには微小線分を曲線に沿って線積分すればよい.チャート上の微小線分をインピーダンスの微小変動と捉えてと書く.そのポアンカレ長は
(9)
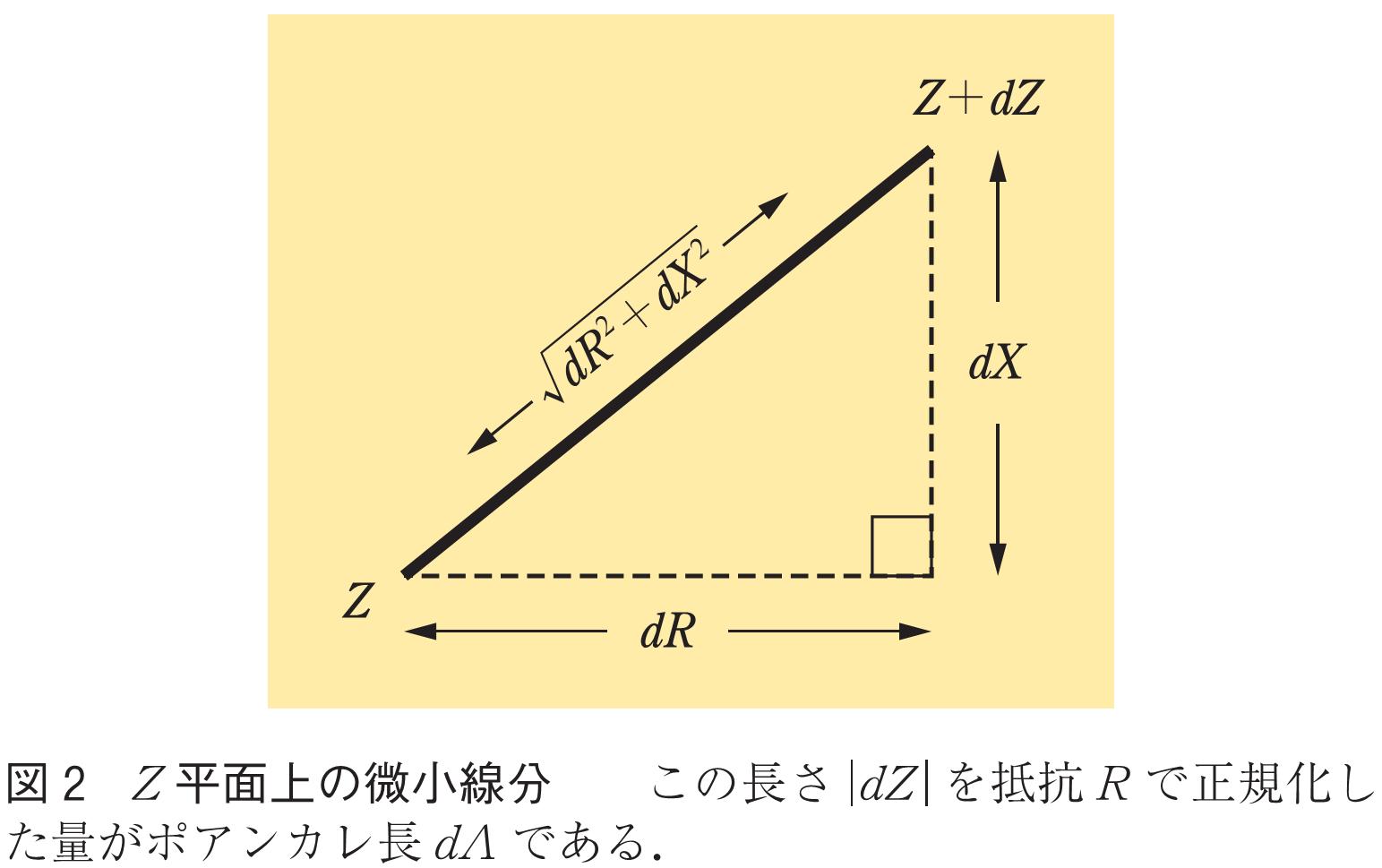
で与えられる(1).第1因子は点
におけるチャートの局所縮尺を意味する(2).第2因子(平方根)は図2に示す
平面上の微小直角三角形の斜辺の長さ
である.つまり見掛けの長さに縮尺を乗じた量がポアンカレ長である.上式の双対としてアドミタンスの微小変動
による表現
(10)
も合わせて覚えておこう.
式(9)または(10)を線積分することで滑らかな曲線の長さが求まる.それにしても平方根の中に変数が二つも含まれている.さすがに手計算は容易でない.が,幸運なことに直列LC回路では積分経路が定円に沿う.なので積分が格段に簡単となる.具体的には式(9)で
として同じ定
円上にある点Aから点Bまで積分する.その結果に式(7)を代入することでポアンカレ長
(11)
が求まる.同様に並列LC回路では積分経路が定円に沿う.式(10)で
として積分すると上式と同じ結果となる.どちらの場合も円弧の始点と終点の絶対
値差でポアンカレ長が計算できる.式(8)と(11)を武器に早速例題にアタックだ.
チャート上で道のりを比較する例を図3に示す.●印の点から出発して○印まで歩く.山頂(点C)経由と50(点D)経由でどちらが近道か.
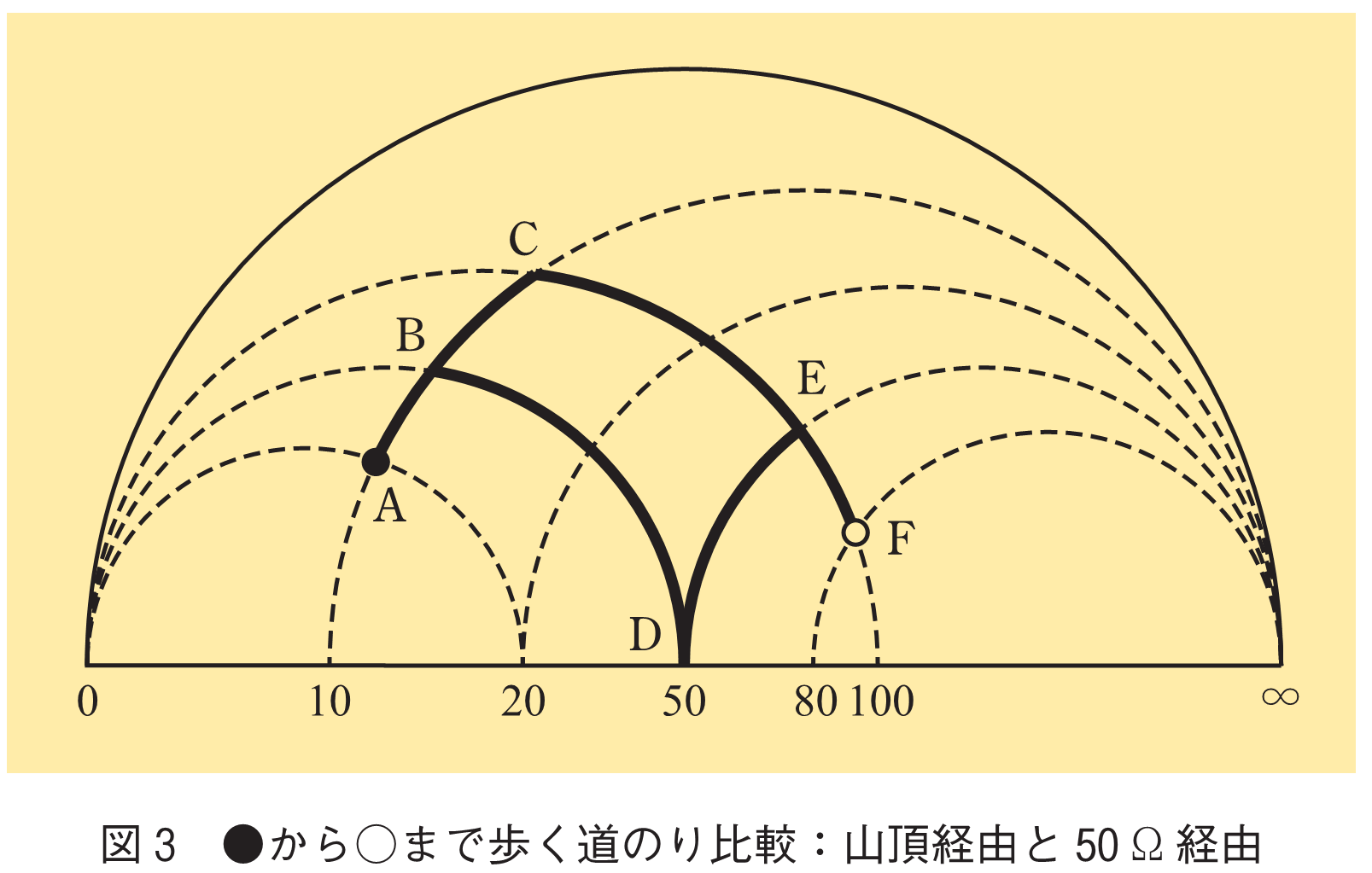
まず山頂経由から考える.3点A,C,Fの値をそれぞれの地平線目盛から読み取り式(8)に代入すると
(12)
となる.これらを式(11)に代入し
(13)
を得る.次に,50経由も同じ手順で
(14)
(15)
となる.つまり長さは相等しい.見た目では山頂経由が明らかに近く見えたが実はそうではなかった.これはチャートの縮尺が一定ではなく場所によって異なっていること(局所縮尺)に起因する(2).
道の長さ判定にファクタの概念が役立つことが分かった.チャートを地形図と見て
値を各地点の標高に例えてみよう.さて
値は一体どのような形の等高線を描くのだろうか.
ここでもやはり出発点は3.の式(4)である.加えてここで反射係数(3)の公式
(16)
を仲間入りさせる.四つの式から,
,
を消去して
(17)
を得る.と
に関して両平方完成型つまりこれは
平面上の円の方程式である.
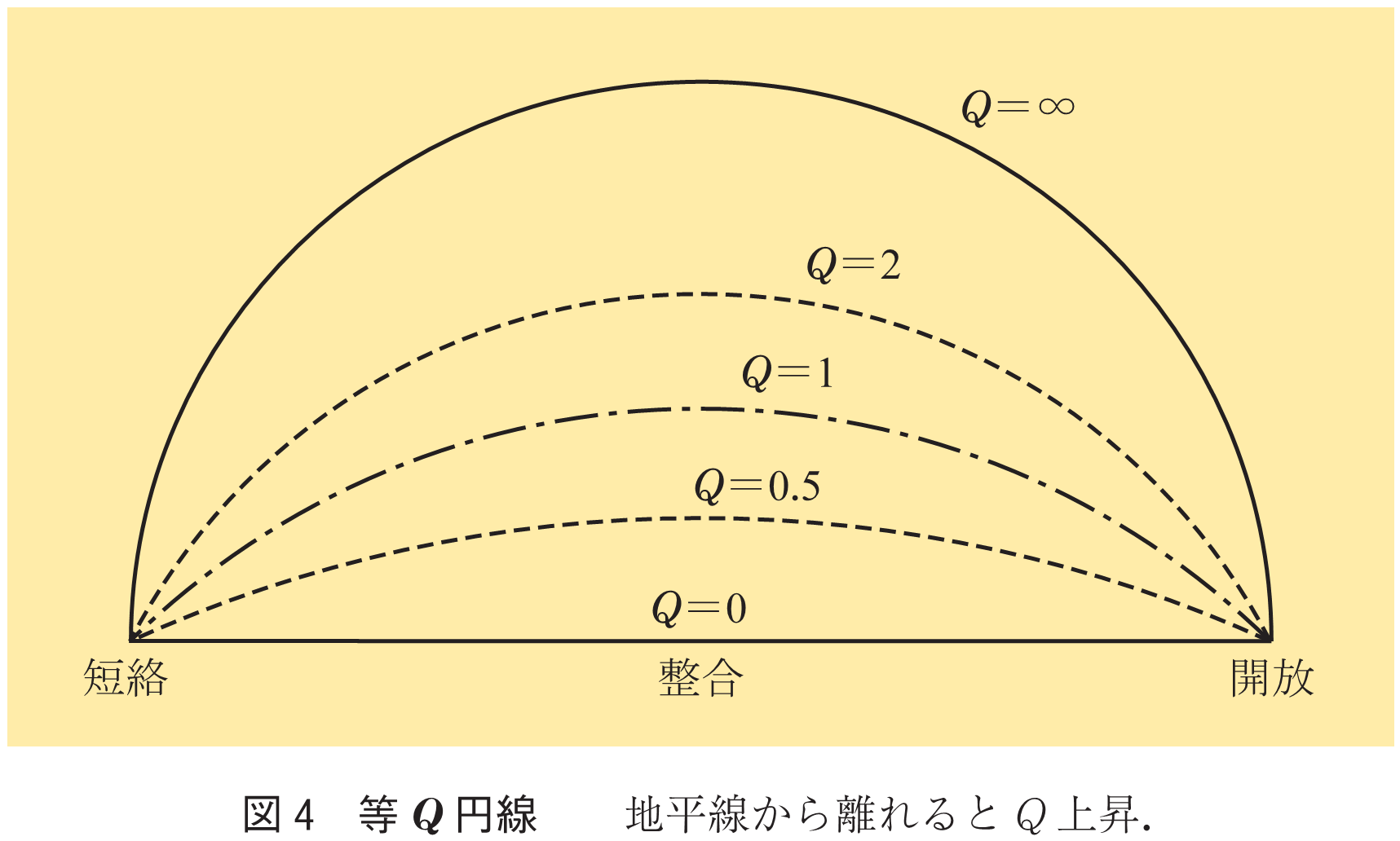
この円を図4にプロットする.平面とは実はスミスチャートのことだったと気づけば合格.
で地平線,
で外周円となる.これらの円と線を一括して等
円線と呼ぶ(筆者小庵が東急沿線).なかでも一点鎖線の円弧
が特別の存在である.これを境界にしてその上下で式(8)の2階偏微分
(18)
の正負が反転する.このことは経路探索の判断材料すなわちLC回路トポロジーを発見する規範となる.
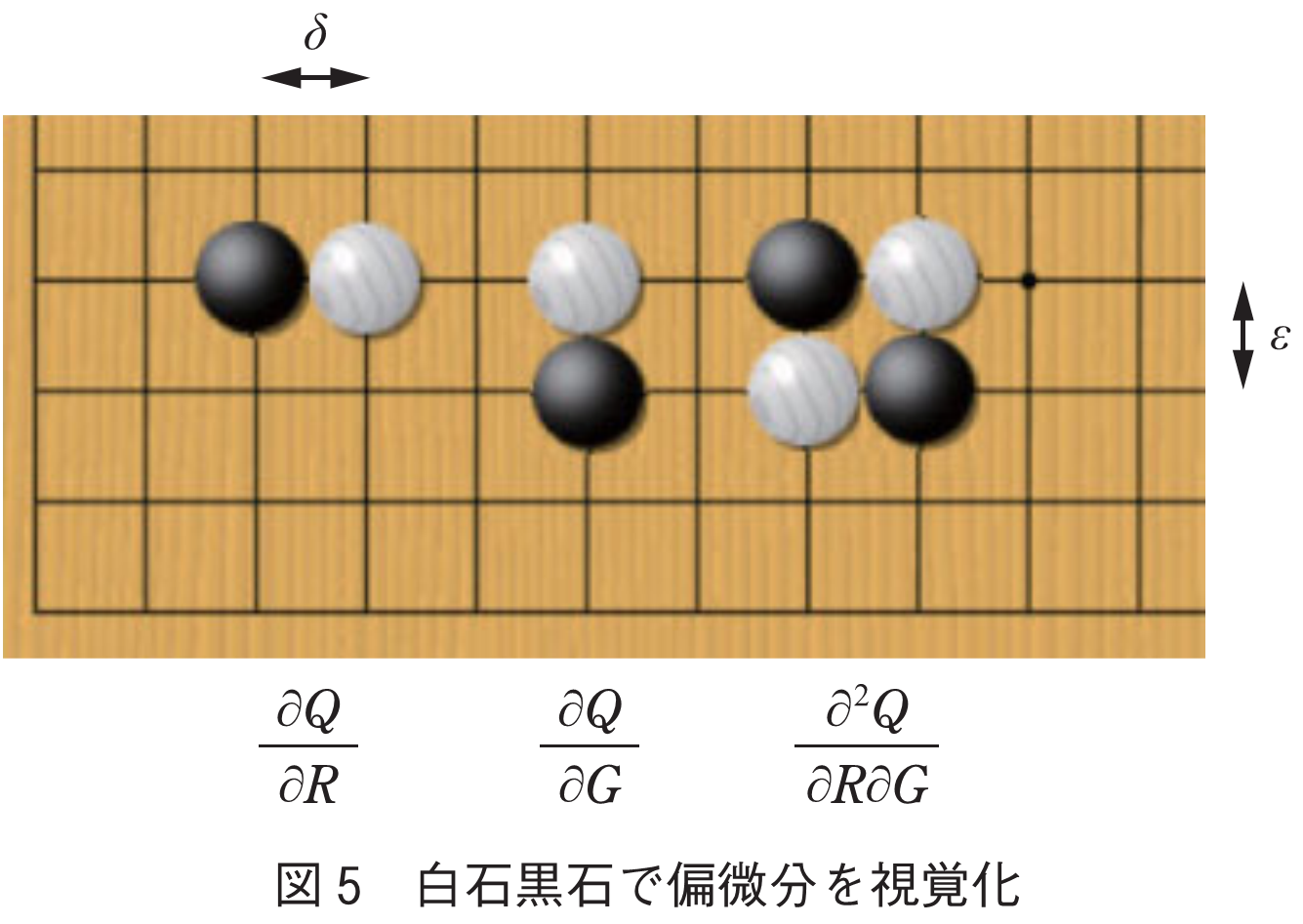
偏微分に苦手意識を感じる学生君のために補足として式(18)左辺の意味を図5に模式化する.横軸縦軸
と見て互いに切り違いの位置にある白石2個の
値の和から黒石2個の
値の和を差し引く.そのまま線間隔
,
を無限に小さくしていった極限値が2階偏微分である.同図1階微分からの類推でなるほどザ・ガッテン!
コイルとコンデンサを意味するLCという記号は集中定数(Lumped Constant)の頭文字とも読める.回路の所望伝送周波数が高くなると集中定数に加えて分布定数の考え方を取り入れることが必要となってくる.分布定数素子の基本である伝送線路にフォーカスしたチャートの歩き方を続編で紹介する.
謝辞 本稿は内閣府SIP「ワイヤレス給電ドローン」と知の拠点あいち「パワー半導体GaNワイヤレス給電」による研究成果を含む.
(1) K. Yamada, “Graphical representation of the power transfer efficiency of lumped-element circuits based on hyperbolic geometry,” IEEE Trans. Circuits Systems Ⅱ, vol.64, no.5, pp.485-489, May 2017.
(2) T. Ohira, “Poincaré length,” IEEE Microw. Mag., vol.21, no.3, pp.120-121, March 2020.
(3) T. Ohira, “Standing wave ratio,” IEEE Microw. Mag., vol.21, no.2, pp.108-109, Feb. 2020.
(2019年12月22日受付)
オープンアクセス以外の記事を読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード