
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|
量子機械学習
5.
変分量子アルゴリズムと量子機械学習
Variational Quantum Algorithms and Quantum Machine Learning
量子コンピュータハードウェアの発展に伴い,量子情報処理によって機械学習を高速化するという方向性の研究が盛んに行われている.近未来の量子コンピュータの能力は様々な面で限られたものになることが予想されるため,それに適したアルゴリズムを設計することが重要であり,近年様々な理論提案・実験実証が行われてきている.本稿では特に,近未来の量子コンピュータの応用方法として注目を浴びている変分量子アルゴリズムに焦点を当て,最近の取組みを概観する.
キーワード:NISQ,量子機械学習,変分量子アルゴリズム,量子コンピュータ
近年の量子コンピュータハードウェアの発展は目覚ましい.2019年にはGoogleのグループが53量子ビットを備えたデバイスを作製し,ある特定のタスクにおいてスーパコンピュータを超えたと発表した(1).ただし「特定のタスク」とは,与えられた量子コンピュータの振舞いをそっくりそのままシミュレートしなさい,というタスクのことで,量子コンピュータにとって非常に有利な問題設定である.なにせ量子コンピュータは単に適当な量子回路を動かすだけでいいのだ.実用的な計算には程遠い.
機械学習の分野においても,既に従来形コンピュータ(古典コンピュータ)上でのベストアルゴリズムを上回る計算量スケーリングを持つ量子アルゴリズムは幾つか知られているが,これらの実用的なアルゴリズムを実行できるハードウェアはまだ現れていない.量子コンピュータが外界からの雑音にとてもぜい弱であり,長時間の計算を行うことができないことが原因である.例えばGoogleのデバイスでも,数十µsの間に一回の計算を終えなければ量子ビットは壊れてしまう.一回のゲート操作に10ns程度の時間が必要なので,多くとも1,000回程度の操作しかできないことになる.このように限られた動作しかできない量子ハードウェアはNISQデバイス(Noisy Intermediate Scale Quantumの略)と呼ばれている.理論的に高速性が保証されたアルゴリズムの中で,最もリソースを割かないと思われている量子化学計算の分野であっても109回以上のゲート操作が必要であると推定されており,NISQデバイスで実行することは不可能である.
量子誤り訂正を実現し,高速性の保証のあるアルゴリズムを実行することが量子情報処理分野の一つの目標だと言える.しかし誤り耐性を持った大規模な量子コンピュータが実現するまでの道のりはまだまだ長い.幾つもの技術的ブレークスルーが必要で,数十年スケールの時間がかかると考えられている.
誤り耐性量子コンピュータを待つのもよいが,せっかく実現したNISQデバイスを何とか活用しようという研究が近年盛んに行われている.NISQデバイスは,量子にとても有利な計算での対決とはいえ,スーパコンピュータを超えることができたのだ.この計算能力を何らかの形で活用しようというのは自然な流れだろう.量子化学計算や最適化,機械学習など様々な応用提案が行われている.
NISQアルゴリズムで一際存在感を放っているのが,変分量子アルゴリズムと呼ばれる一連の手法である.本稿では,機械学習のための変分量子アルゴリズムを中心に,NISQでの量子機械学習(用語)アルゴリズムを解説する.また,NISQアルゴリズムに機械学習で知られている手法を応用し,性能を向上させようという方向性についても紹介したい.更に本稿の最後には,量子コンピュータ実機を使った量子機械学習実験の最近の動向を述べる.
変分量子アルゴリズムとは,量子回路の出力を適宜モニタしながら,古典コンピュータによってその構成を逐次調整し,目的のタスクを実行できる量子回路を作り出すアルゴリズムのことである.その調整は,機械学習と同じように,目的のタスクに合わせて設計したコスト関数を最小化することで達成する.量子コンピュータと古典コンピュータを協働させる方式から,量子・古典ハイブリッドアルゴリズムと呼ばれることもある.図1にその概要を示した.中心となるアイデアは,古典コンピュータでできることは古典コンピュータでやってしまい,本当に量子性が必要そうな計算のみを量子コンピュータにやらせることで,量子コンピュータの負荷を少しでも減らそうとすることである.元々は量子化学計算にNISQデバイスを応用するための一手法として開発されたが,その考え方は後に大きな広がりを見せ,今ではNISQの機械学習応用にもつながっている.調整するパラメータとしては,ハードウェア上で精度良く調整できる一量子ビット回転ゲートの角度を使うことが多い.
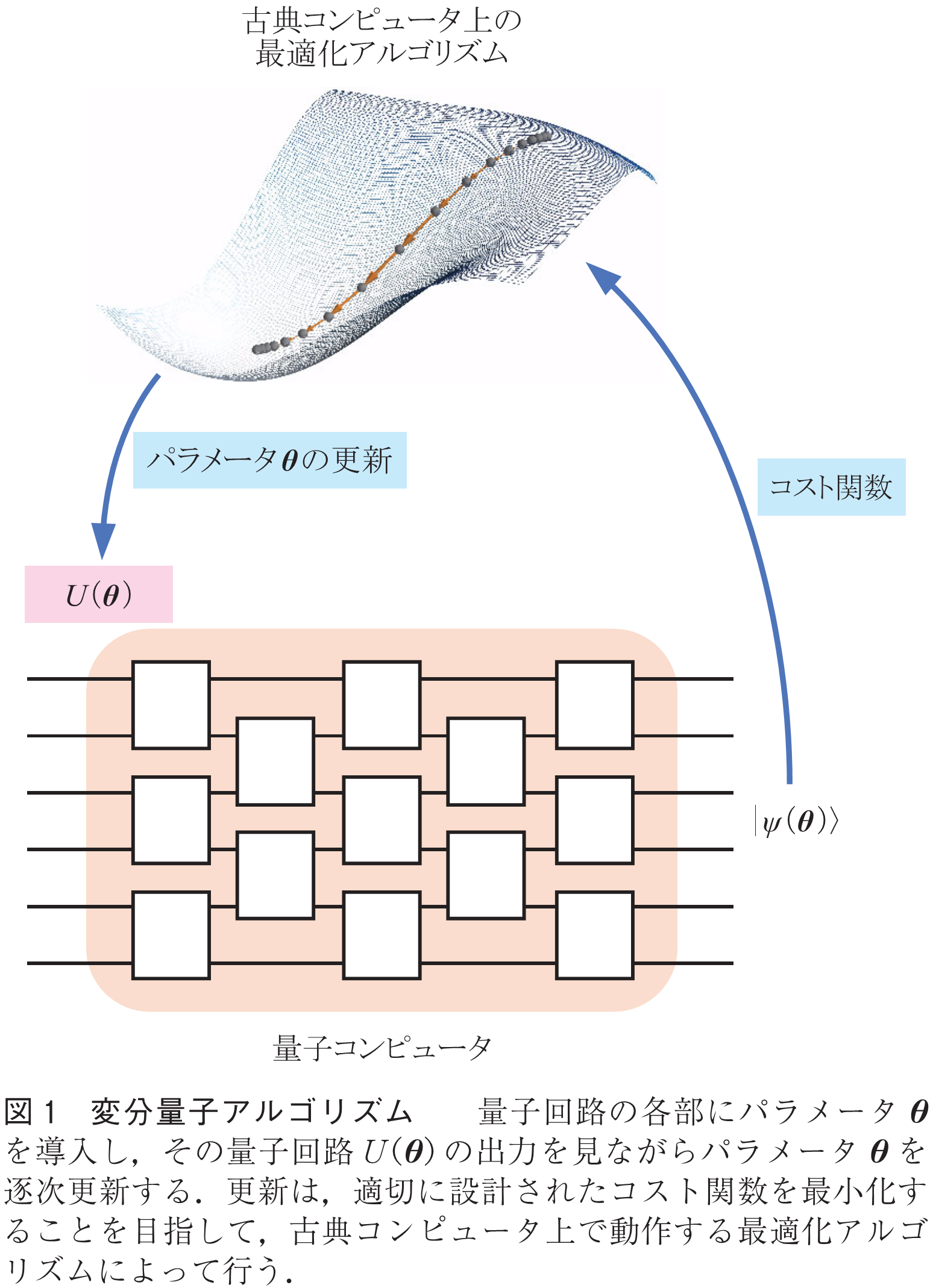
変分量子アルゴリズムの最大の長所は,量子回路の形を実在しているハードウェアで実行可能なものに固定したまま,そのパラメータを調整することで,所望のタスクを達成しようとするところにある.実際のNISQデバイスには,量子ビット間の接続性や量子情報の持続時間など様々な制約があり,実行できる量子回路には制限が課される.例えば10µsで壊れてしまう量子ビットを使うなら,10µs以内に終えられる量子回路しか実行できない.変分量子アルゴリズムではこのような制約を満たす範囲で回路を最適化するという戦略を取れる.通常の量子アルゴリズムが,ある決まった複雑な回路を実行しなくてはならないことと,この点が大きく異なる.もちろん,制約に合わせると実行できる回路の性能は落ちる.しかしGoogleの実験でも示されたように,NISQデバイスはこのような制約の下であっても,スーパコンピュータでシミュレートが困難であるような量子回路を実行可能だ.したがって全く同じことを古典コンピュータで実行することは難しいだろう.これも変分量子アルゴリズムの長所であるといえる.
一方でその短所は,これまでの多くの量子アルゴリズムと異なり,理論的高速性が全く保証されていないという点である.一般の量子回路の古典的なシミュレートは困難であるが,だからといって与えられた問題に対して古典コンピュータよりも高速に良い解を与えるとは限らない.理論的な保証がない以上,数値的・実験的な検証が必要となるが,後に述べるようにまだまだ進んでいないのが現状である.更に大規模な検証が求められている.
機械学習のために提案された変分量子アルゴリズムの一例として,筆者らが提案した量子回路学習(2)を紹介する.量子回路学習は,NISQデバイス上で生成できる量子状態を特徴量の保存に利用し,その特徴量をまた別の量子回路によって適切に選択して出力するアルゴリズムである.ここで特徴量とは,与えられた入力データの「特徴」をつかむために,適切に
を変換した量
のことを言う.図2にその概念図を示した.図2左のデータは線形分離できないが,それを特徴写像
によって図2右のように高次元の空間に写すことで,線形分離できるようになる.このように,得られたそのままのデータでは簡単にできなかった機械学習タスクが,高次元の特徴量空間にデータを写すことによって簡単にできるようになることはよくある.そこで,
量子ビットの量子状態が
次元の複素ベクトルと等価であることに着目し,量子状態に
次元の特徴量を埋め込もうというのが量子回路学習である.
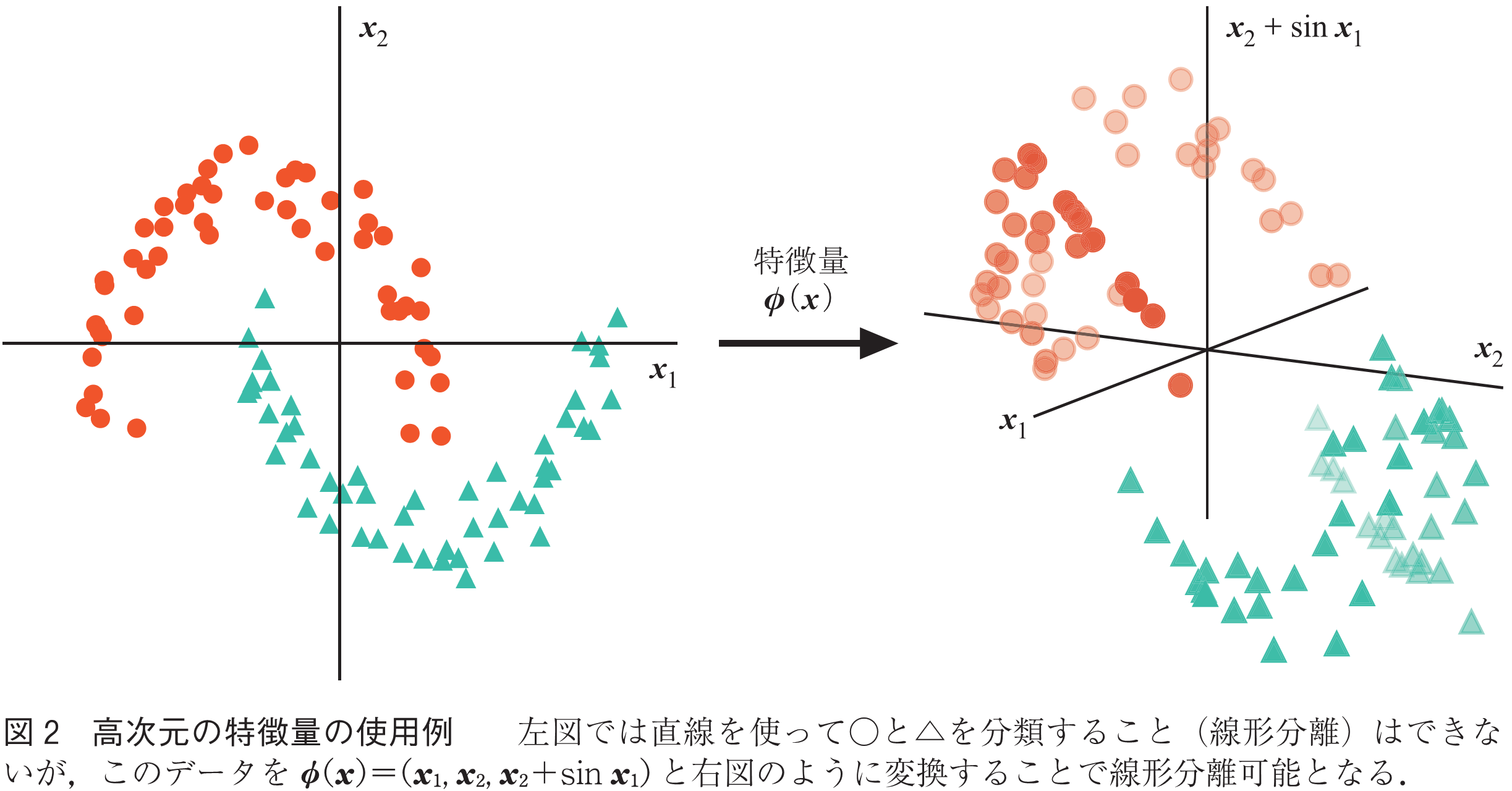
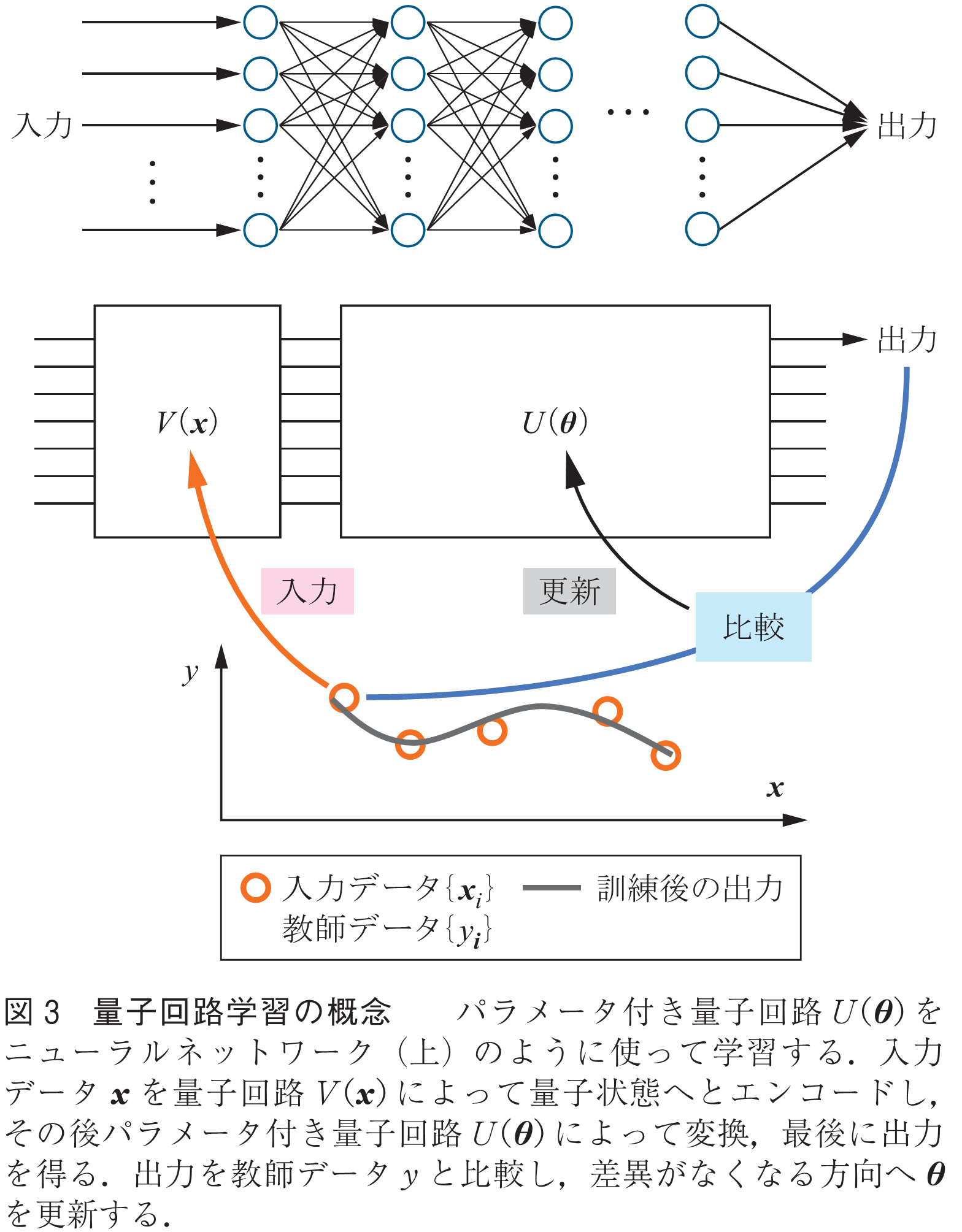
図3に量子回路学習アルゴリズムの概要を示した.その大まかなアルゴリズムは以下である.
①与えられた入力データを,ある適当な量子回路
を用いて,量子状態
にエンコードする.
②パラメータ付き量子回路をニューラルネットワークのように用いて,パラメータを持った量子回路
を作用させて状態を変換する.
③出力状態の適当な量子ビットを測定して,例えば1ビット目が0となる確率を求める.この際,一つの量子ビットを測定したときに出てくる結果は,0・1のどちらかしかないので,2の状態準備を繰り返し行い,測定を平均化する必要がある.
④③で得られた値を古典コンピュータ上で教師データと比べる.比較には例えば二乗誤差などのコスト関数を用いる.
⑤比較結果に基づいて,パラメータを更新し,①に戻る.
ここで量子回路学習がどのような構造を持っているか吟味しよう.入力データはまず
次元のベクトルである
に写される.次に量子回路
をかけるわけだが,これは上記のベクトルに
次元の行列を作用させて,新たなベクトルを作り出すことに相当する.量子回路学習はこの行列を調整することにより学習を行うアルゴリズムだ.したがってその本質は単なる高次元空間での線形回帰である.ただし,
次元の行列が全て使えるわけではなく,使える行列はNISQデバイスが扱える量子回路で表現できるものに限られる.この制限は量子回路学習で構築できる機械学習モデルの表現能力を落とすものの,逆に正則化のような働きをして過学習を防いでくれるかもしれない.
数値的・実験的には,現在までのところ,簡単な機械学習タスクが行えることをデモンストレーションするにとどまっており,実用には程遠い状況である.しかし,このアルゴリズムであればNISQデバイス上でも実行できるかもしれないという期待の下,研究が盛んに進められている.
量子コンピュータからの出力は全て確率的で,量子回路の出力状態を測定すると,ビット列がある確率分布に従ってランダムに得られる.量子回路学習では測定を何度も繰り返し,平均化したものを出力として用いるため,その際平均以外の情報は捨ててしまうことになる.そこで,量子コンピュータで生成される確率分布を直接使えるような良い応用先がある.それが機械学習の一大分野,生成モデルである.
生成モデルは,実世界で得られるあるデータが,背後に存在する確率分布
からのサンプルであるという仮定に基づいて,その確率分布を再現するようなモデル
を構成しようとするものだ.真の確率分布
をよく再現するようなモデル
ができれば,そのモデルは現実には(まだ)得られていない,存在しないデータを生成できる.敵対的生成ネットワークはその代表例で,現在では画像生成のタスクに広く応用されている.
このモデルに,量子的なデバイスにしか生成できない確率分布を使おうという提案が盛んになされている(3).このアプローチでは,パラメータ付き量子回路
によって生成される量子状態の確率分布を,データセット
に最も適合するようにパラメータ
を調整していく.一般の量子回路からのサンプリングを古典的にシミュレートすることは困難であると考えられているため,少なくとも同じことを古典コンピュータでやることは難しい.しかしながら,そのような確率分布が,現実のデータセットを表現するために必要かどうかは更なる検証が必要だ.
この方向性では,古典コンピュータ上でのニューラルネットワークを用いた生成モデルとのアナロジーから,様々な研究がなされている.例えば敵対的生成ネットワークやオートエンコーダの「量子版」が提案されている.これからも,機械学習分野で有力な手法の量子版を作り出す流れは続いていくだろう.
様々な応用先に拡張されてきた変分量子アルゴリズムだが,量子回路の最適化を困難にする問題が指摘されている.何も考えなしに,ランダムなパラメータ付き量子回路を構成してしまうと,高い確率で勾配がほぼゼロになってしまうという問題である.これは「ランダム」な量子状態がとても没個性的であり,どんな測定をしてもほとんど同じ結果しか返さないことに起因する.したがって,何らかの戦略に基づいた量子回路の設計が必要とされている.これは変分量子アルゴリズムの実応用をするためには避けて通れない問題であり,筆者らもその解決案を提案してはいるが,いまだこれを完全に解決する戦略は得られていない.
ここまでで,変分量子アルゴリズムをどのようにして機械学習に応用していくかを見てきた.しかし最近は逆に,機械学習で有力となっている最適化手法を変分量子アルゴリズムに適用しようという動きも見られる.
その代表例として,確率的勾配降下法(SGD, Stochastic Gradient Descentの略)がある(4).SGDはデータセットに含まれているデータの数が非常に多いときに有効な最適化手法で,データセットの中からランダムに幾つかのデータを選び出しながら,逐次パラメータを更新していく方法である.図4にSGDの大まかな流れを示した.データ数が多いときには,全てのデータを使って更新方向を決めると計算時間がかかり過ぎるという問題が生じるため,このような手法が使われる.
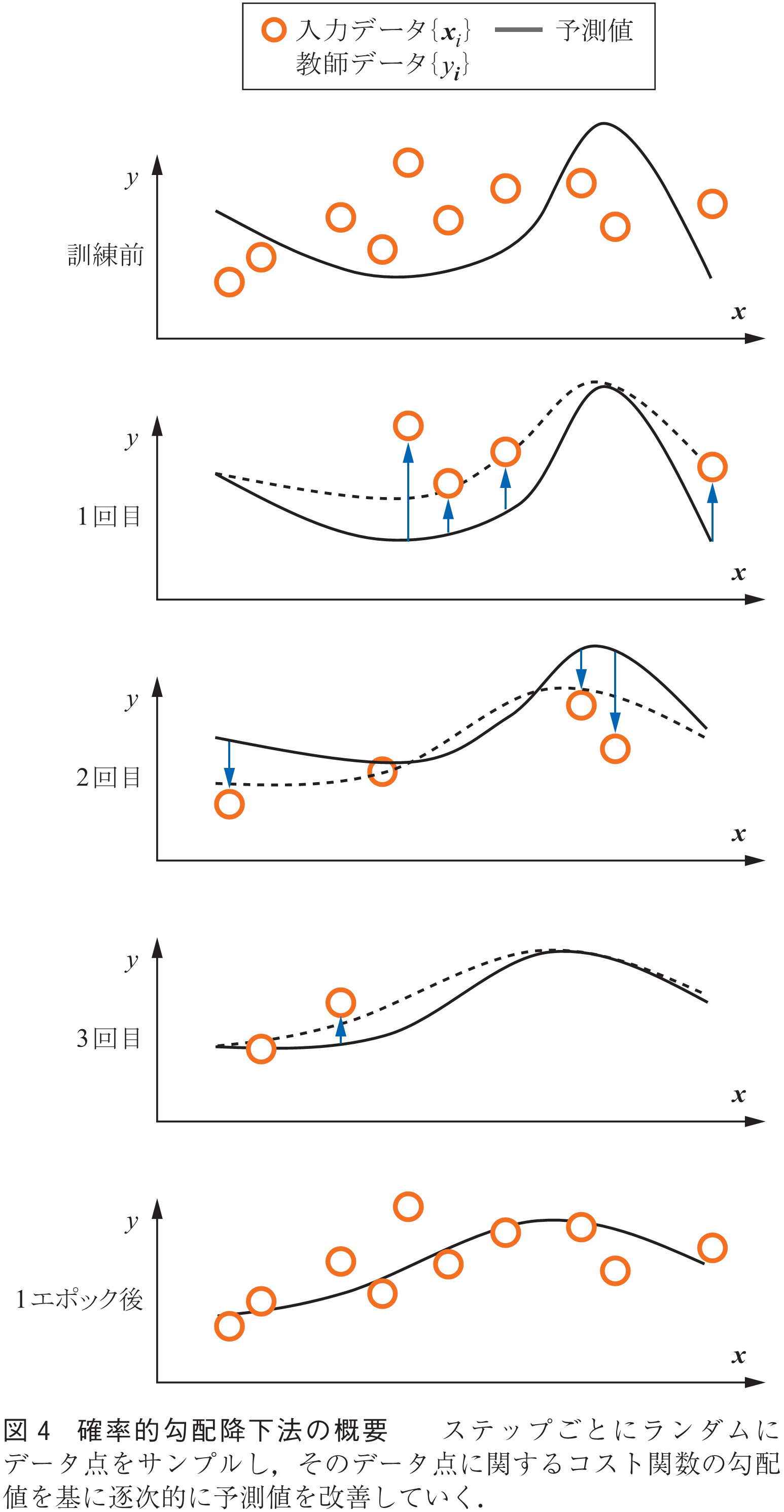
この手法を変分量子アルゴリズムへと応用し,量子回路のパラメータの最適化を高速化しようというわけである.SGDをそのまま変分量子アルゴリズムに適用すると,確率的に行われる部分が二つ現れる.データをランダムに選択する部分と,量子回路からの出力を測定する部分である.このことから,変分量子アルゴリズムに適用したSGDは二重確率的勾配降下法(Doubly Stochastic Gradient Decent)と呼ばれることもある.
SGDを変分量子アルゴリズムに適用すると,多量のデータに対する対策となることに加えて,もう一つの大きな恩恵が得られる.それは,量子回路の出力をパラメータ更新のために平均化する必要がなくなることだ.SGDの収束性は,各更新で使う勾配の値が,真の勾配(全てのデータを使って,無限回の測定によって厳密な平均値を得た場合の値)の不偏推定量になってさえいれば保証される(注1).極端には,あるデータに対して1回だけ量子回路を実行して,得られた一つのビット列を基に更新していくことも可能だ(注2).これは学習に必要な時間を大幅に小さくする可能性を秘めている.
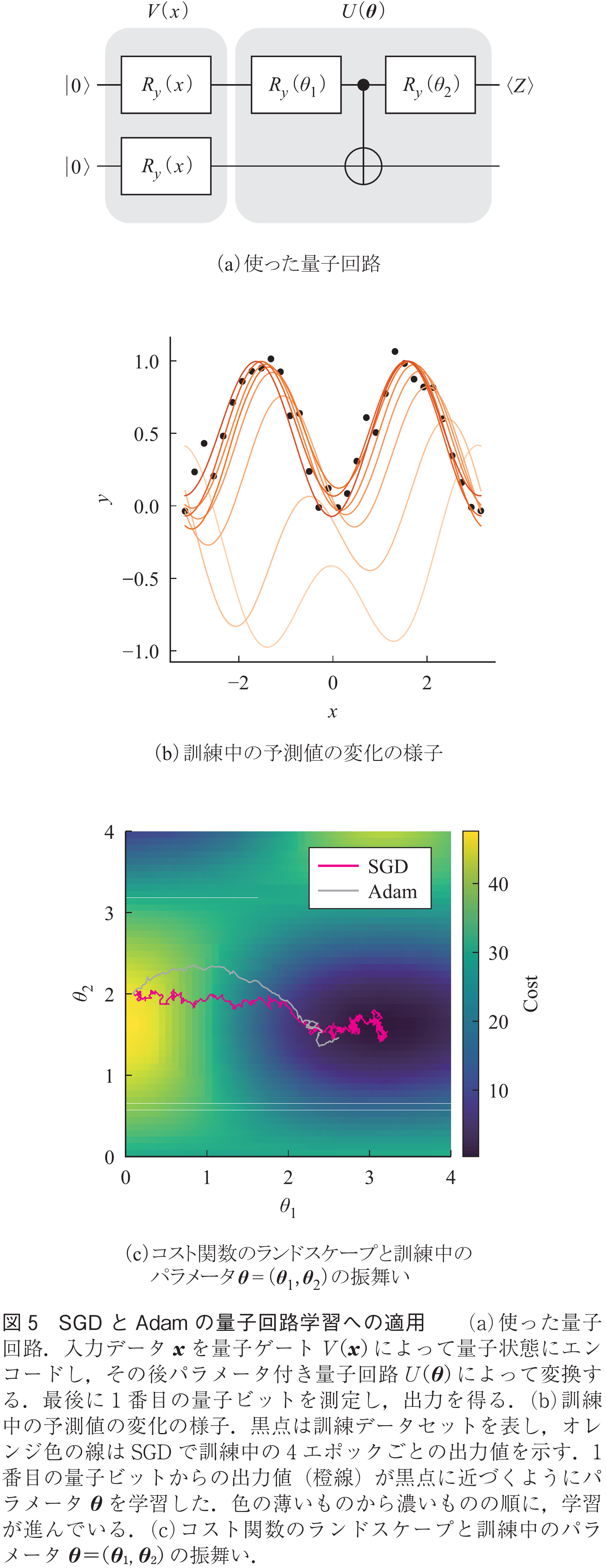
もちろんSGDだけではなく,Adamなどの現代的な最適化手法も同様に適用可能である.例として,3.1の量子回路学習にSGDとAdamを適用したものを図5に示す.をフィッティングするという簡単なタスクを,2量子ビットの量子回路を用いて実行した.この例では,各ステップでデータを1点だけサンプルし,そのデータに対して1回だけ量子回路を実行して最適化を行った.このような極端な戦略をとっても,しっかりと学習が行えていることが見て取れる.機械学習のタスクとしてはとても簡単な例ではあるものの,確率的勾配降下法の有効性を確認できるだろう.
NISQデバイスを機械学習に応用するためのアルゴリズムは,変分量子アルゴリズムだけではない.もう一つの有力な手法として,量子カーネル法(5)がある.量子カーネル法は,古典コンピュータにおける強力な機械学習手法であるカーネル法の量子版である.そこでまずは普通のカーネル法についておさらいしよう.
図2のように元のデータから見て非線形な変換を要求する機械学習タスクを考えよう.図2の例であれば,という変換で一つの軸を足すだけでうまく線形分離することができたが,一般にはもっと高次元の空間に写さなければうまく行かないこともあるだろう.かといって,
の次元を大きくすればするほど,モデルの訓練は困難になる.次元を大きくし過ぎれば,あるデータ
に対して
を計算すること自体が難しくなっていくからだ.
そこで,特徴量間の内積のみで学習を行えるように,問題を適切に変換するのがカーネル法である.カーネル法では,ある二つのデータと
について,
と
の内積(カーネル関数)
が効率的に計算できることのみを仮定する.
があらわに計算できなくても,その内積が計算できればよいということだ.これにより無限次元の空間でさえも,機械学習に適用できるようになる.例えばよく使われるガウシアンカーネルは,無限次元の
を使うことに対応する.カーネル法では,訓練データセットの全ての組合せについて
を計算し,その後その値のみを使って,回帰・分類等の学習を行う.
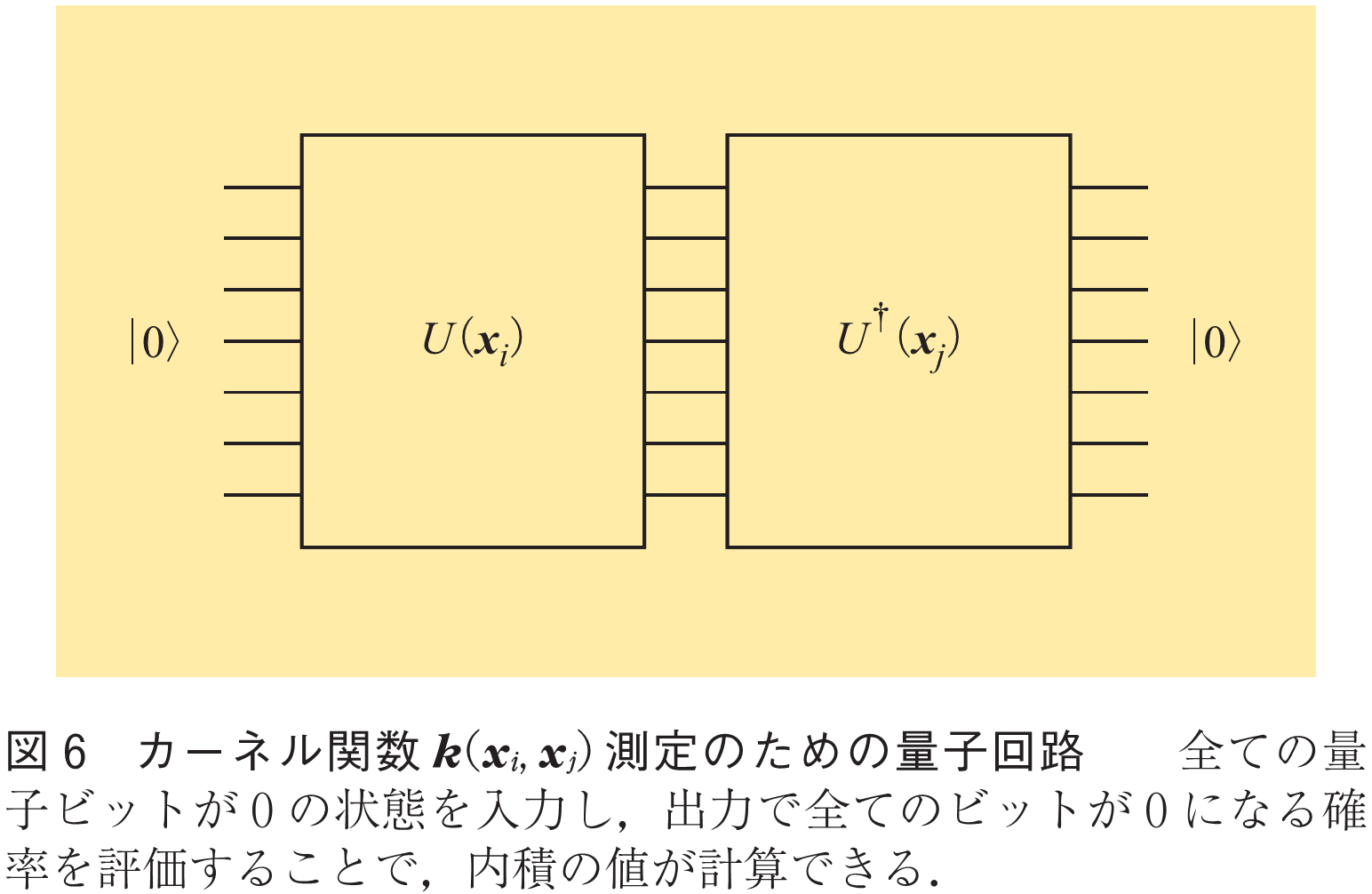
ところで,量子状態は高次元のベクトルと等価で,量子回路学習では量子状態を高次元の特徴量ベクトルの保存に利用していた.そこで,量子コンピュータ上で量子状態間の内積(=特徴量ベクトル間の内積)を計算できれば,カーネル法に簡単に接続できる.これを量子カーネル法と呼んでいる.量子状態間の内積は,量子コンピュータ上で比較的簡単に評価できる.データをエンコードする量子回路を
とすると,図6のような回路で測定が可能である.量子カーネル法では,まずこの回路によって,全てのデータの組
,
についてカーネル関数
を評価する.その後,通常のカーネル法と同じように,回帰・分類等の目的に合わせて学習を行う.
量子カーネル法と変分量子アルゴリズムによる機械学習の最も異なるところは,逐次的な量子回路のパラメータ最適化の有無である.変分量子アルゴリズムにおけるパラメータ最適化には,勾配消失などの大きな問題が立ち塞がっていて,大規模な実験を行うことができていない.一方で量子カーネル法は,とにかく図6の回路を実行できさえすればよく,大規模な実験実証につなげやすいという利点がある.
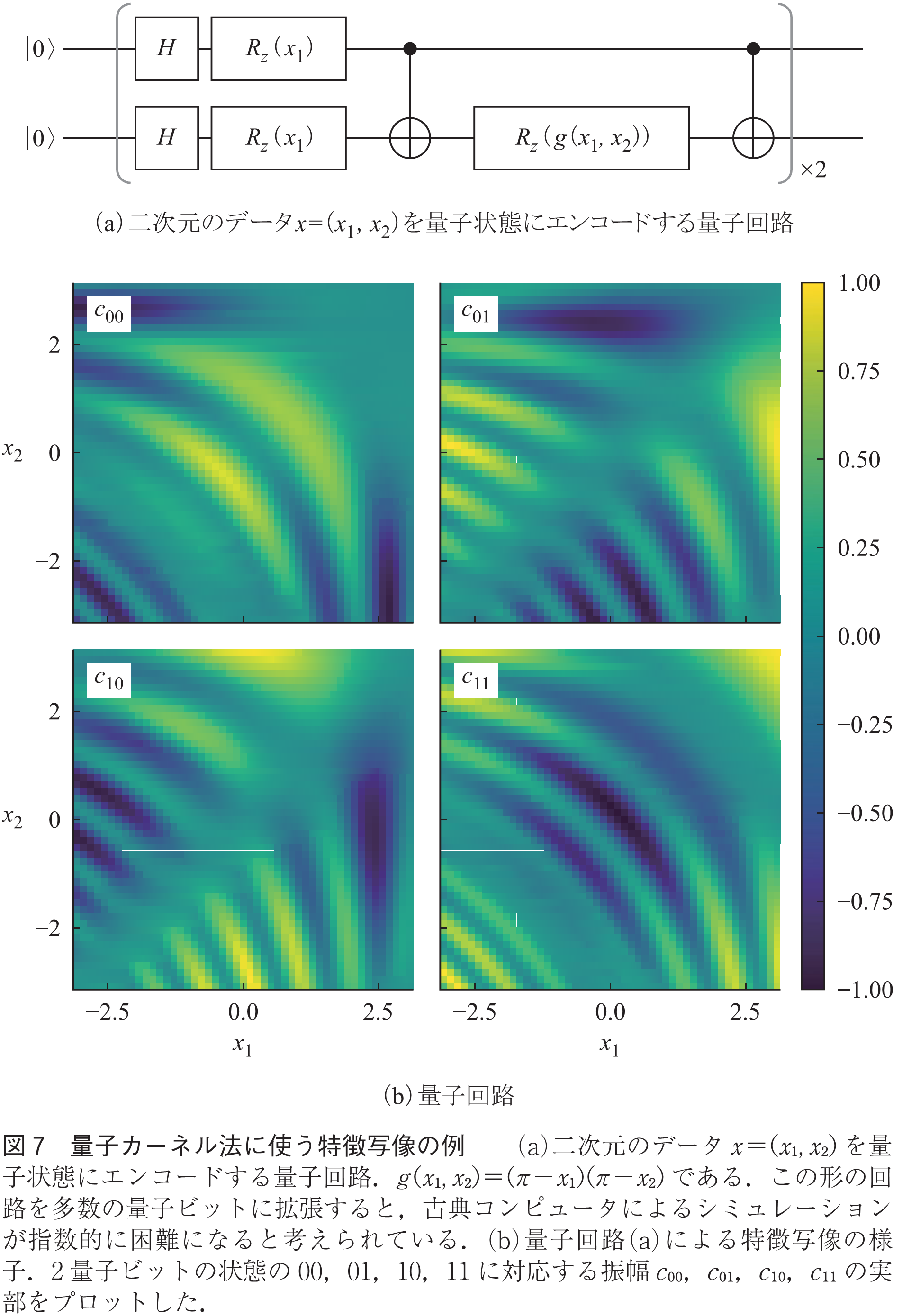
ただし,量子カーネル法では,古典コンピュータからの優位性を保つため,古典コンピュータでは計算が困難であろうと予想されるカーネル関数を使うことが求められる.IBMのグループは,図7(a)のような量子回路をとして使うことを提案した(5).この量子回路が表す特徴写像を併せて図7(b)に示した.2量子ビットであれば図7(b)のように簡単にシミュレートできてしまうが,同じような回路を数十量子ビットにスケールアップすれば,古典コンピュータによるシミュレーションが困難になると信じられている.かと言って,古典的に計算が困難な内積をカーネル関数として使うことが,実応用に恩恵をもたらすかどうかは不透明で,今後検証が必要である.
最後に,ここまでに紹介したアルゴリズムについて,最新の実験の動向を紹介しよう.まず変分量子アルゴリズム全般を見渡すと,これまでで最も多くの量子ビット数を使った実験は,2021年のGoogleによるもの(6)である.この実験では,23量子ビットを用いて,グラフ上の最適化問題が解かれた.量子回路学習については,IBMのグループが2018年に超伝導デバイスで2量子ビットの実験を行った(5)後,これといった進展は見せていない.生成モデルでは,イオントラップで8量子ビットを用いた実験が2020年末に発表された(7).変分量子アルゴリズムによる機械学習のデモンストレーションとしては最大規模の実験である.この実験では,量子デバイスを用いた敵対的生成ネットワークによって,手書き文字の生成モデルが構成された.量子カーネル法は,その実装の簡単さから比較的大規模な実験が進んでおり,筆者らも2021年に25量子ビット相当のダイナミクスを利用した実験を発表した(8).また,IBMのグループからも,同年27量子ビットを使った実験が発表されている(9).
このように,少しずつ大規模な実験ができるようになってきているのは確かである.一方で,30量子ビット程度までの量子コンピュータは,通常のワークステーションでシミュレート可能な範ちゅうなので,まだ何らかの意味で古典コンピュータを超えたと言えるような量子機械学習実験はできていないのも事実だ.
本稿では,主に変分量子アルゴリズムに焦点を当て,NISQデバイス向けの量子機械学習手法について概観した.様々な理論提案はなされているものの,実応用できるかどうかは全く分かっていない.しかし逆に,まだまだ研究の余地が残されている新しい分野とも考えられる.量子情報処理の分野は,比較的参入障壁が高い分野だと捉えられることが多いように思うが,最近では(少し過熱気味の)量子コンピュータブームもあいまって,量子情報を勉強する環境(10),(11)も整ってきていると感じる.量子情報の分野は近年常に人不足なので,興味のある読者は是非参入してみてほしい.
(1) F. Arute, K. Arya, R. Babbush, D. Bacon, J.C. Bardin, R. Barends, R. Biswas, S. Boixo, F.G.S.L. Brandao, D.A. Buell, B. Burkett, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M.P. Harrigan, M.J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T.S. Humble, S.V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P.V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà, J.R. McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M.Y. Niu, E. Ostby, A. Petukhov, J.C. Platt, C. Quintana, E.G. Rieffel, P. Roushan, N.C. Rubin, D. Sank, K.J. Satzinger, V. Smelyanskiy, K.J. Sung, M.D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z.J. Yao, P. Yeh, A. Zalcman, H. Neven, and J.M. Martinis, “Quantum supremacy using a programmable superconducting processor,” Nature, vol.574, no.7779, pp.505-510, Oct. 2019.
(2) K. Mitarai, M. Negoro, M. Kitagawa, and K. Fujii, “Quantum circuit learning,” Phys. Rev. A, vol.98, no.3, 032309, Sept. 2018.
(3) M. Benedetti, D. Garcia-Pintos, O. Perdomo, V. Leyton-Ortega, Y. Nam, and A. Perdomo-Ortiz, “A generative modeling approach for benchmarking and training shallow quantum circuits,” npj Quantum Information, vol.5, no.1, p.45, May 2019.
(4) R. Sweke, F. Wilde, J. Meyer, M. Schuld, P.K. Faehrmann, B. Meynard-Piganeau, and J. Eisert, “Stochastic gradient descent for hybrid quantum-classical optimization,” Quantum, vol.4, p.314, Aug. 2020.
(5) V. Havlíček, A.D. Córcoles, K. Temme, A.W. Harrow, A. Kandala, J.M. Chow, and J.M. Gambetta, “Supervised learning with quantum-enhanced feature spaces,” Nature, vol.567, no.7747, pp.209-212, March 2019.
(6) M.P. Harrigan, K.J. Sung, M. Neeley, K.J. Satzinger, F. Arute, K. Arya, J. Atalaya, J.C. Bardin, R. Barends, S. Boixo, M. Broughton, B.B. Buckley, D.A. Buell, B. Burkett, N. Bushnell, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, S. Demura, A. Dunsworth, D. Eppens, A. Fowler, B. Foxen, C. Gidney, M. Giustina, R. Graff, S. Habegger, A. Ho, S. Hong, T. Huang, L.B. Ioffe, S.V. Isakov, E. Jeffrey, Z. Jiang, C. Jones, D. Kafri, K. Kechedzhi, J. Kelly, S. Kim, P.V. Klimov, A.N. Korotkov, F. Kostritsa, D. Landhuis, P. Laptev, M. Lindmark, M. Leib, O. Martin, J.M. Martinis, J.R. McClean, M. McEwen, A. Megrant, X. Mi, M. Mohseni, W. Mruczkiewicz, J. Mutus, O. Naaman, C. Neill, F. Neukart, M.Y. Niu, T.E. O’Brien, B. O’Gorman, E. Ostby, A. Petukhov, H. Putterman, C. Quintana, P. Roushan, N.C. Rubin, D. Sank, A. Skolik, V. Smelyanskiy, D. Strain, M. Streif, M. Szalay, A. Vainsencher, T. White, Z.J. Yao, P. Yeh, A. Zalcman, L. Zhou, H. Neven, D. Bacon, E. Lucero, E. Farhi, and R. Babbush, “Quantum approximate optimization of non-planar graph problems on a planar superconducting processor,” Nat. Phys., vol.17, no.3, pp.332-336, Feb. 2021.
(7) M.S. Rudolph, N.B. Toussaint, A. Katabarwa, S. Johri, B. Peropadre, and A. Perdomo-Ortiz, “Generation of high-resolution handwritten digits with an ion-trap quantum computer,” arXiv: 2012.03924, Dec. 2020.
(8) T. Kusumoto, K. Mitarai, K. Fujii, M. Kitagawa, and M. Negoro, “Experimental quantum kernel trick with nuclear spins in a solid,” npj Quantum Information, vol.7, p.94, 2021.
(9) J.R. Glick, T.P. Gujarati, A.D. Corcoles, Y. Kim, A. Kandala, J.M. Gambetta, and K. Temme, “Covariant quantum kernels for data with group structure,” arXiv: 2105.03406, May 2021.
(11) M. Schuld and F. Petruccione, 量子コンピュータによる機械学習,荒井俊太,篠島匠人,高橋茶子,御手洗光祐,山城 悠,大関真之(訳),共立出版,東京,2020.
(2021年5月31日受付 2021年6月17日最終受付)
■ 用 語 解 説
(注1) 厳密には,コスト関数が数学的に良い性質を持っていることも条件となる.
(注2) ただし,例えば現状の超伝導量子ビットの場合,量子ビットを制御するFPGAと古典コンピュータの通信に最低でも1ms程度かかる一方で,量子回路は1回10µs程度で実行できてしまうため,1回ごとにパラメータを更新するのはもったいない.現実的にはデバイスの特性に合わせて最適化する必要がある.
オープンアクセス以外の記事を読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード