1．は　じ　め　に

　反強磁性体は，原子スケールでミクロな磁化を有するが，隣り合う磁化が互いに打ち消し合うように整列しているため，全体として自発磁化を持たない．その性質から，強磁性体に比べて，磁化方向を制御・検出することが一般的に困難であると考えられてきた．しかしながら，最近の研究結果から，強磁性体と同様に，スピン流と反強磁性体の磁化との相互作用が存在することが示され，スピン流による反強磁性体の磁気モーメント方向の制御^(1),(2)，磁気抵抗効果^(3),(4)，反強磁性体中のスピン流伝送^(5),(6)，磁化のダイナミクスの励起などの研究が活発に行われている．これらの研究の進展を踏まえて，反強磁性体が次世代スピントロニクスにおける新材料として認識されつつある⁽⁷⁾．反強磁性体の最も魅力的な特性の一つに，THz帯域に達する高い共鳴周波数がある．これは，反強磁性共鳴周波数が分子場の平方根に比例するためで，通常の強磁性体における強磁性共鳴（GHz帯域）に比べて圧倒的に高い．古くから遠赤外光源を利用した反強磁性共鳴測定が行われているが⁽⁸⁾，測定精度の問題で共鳴線幅等の共鳴特性の詳細な評価が困難であった．最近のTHz技術等を含む様々な測定・計測技術の急速な発展により，THz帯において時間領域や周波数領域で高精密・高分解能な評価ができるようになってきた^(9)～(11)．これまで実験的に未開拓であった反強磁性磁化ダイナミクスの緩和機構などが調査されつつある⁽¹¹⁾．これらの研究は，次世代の高速通信などへの応用を見据え，ごく最近盛んに行われている．

　本稿では，典型的なコリニア反強磁性体であるNiOを取り上げ，反強磁性共鳴及びTHz分光の基礎⁽¹¹⁾から，反強磁性共鳴の制御手法⁽¹²⁾や反強磁性体におけるスピンポンピング効果⁽¹³⁾についての最近の研究結果について紹介する．

2．反強磁性共鳴

　まず，反強磁性ダイナミクスを議論する上で重要となる反強磁性共鳴の基礎について解説する．

　二つの磁気副格子を有し，それぞれの副格子の磁気モーメントが反平行に結合しているようなコリニア反強磁性体を考える．このような磁気構造を持つ代表的な材料にNiO，CoO，MnO等がある．副格子をA及びBとし，それらに付随する磁気モーメント（単位ベクトル）を及びとすると，これらのダイナミクスは以下で記述される⁽¹⁴⁾．

ここで，及びはそれぞれの副格子における磁気回転比，及びはそれぞれの副格子内でのダンピング定数，及びは副格子間のダンピング定数である．更に，副格子A及びBに作用する有効磁界は以下で記述される．

ここで，はそれぞれの副格子に付随した磁化の大きさ及び異方性エネルギーで，は分子場定数，は周波数の励起磁界の大きさである．及びは磁気異方性及び励起磁界の方向を決める単位ベクトルである．以下で紹介する実験は全て外部静磁界なしで行っているため，簡単のためここでは静磁界の項は含めていない．NiOの場合，両副格子ともNi^2＋カチオン^(用語)に付随した磁気モーメントで構成されており，副格子の磁化の大きさ，及び異方性エネルギーは同じなので，，とする．ダンピング定数は副格子内でのダンピングのみを考慮し，とする．微小振動を仮定し，式(１)及び(２)を線形化すると以下の連立方程式が得られる．

ここで．は円偏向の極性を示す．式(４)をそれぞれ，について解くと，

及び，

となる．ここで，は反強磁性共鳴周波数である．つまり，共鳴周波数が分子場定数の平方根に比例していることが分かる．更に，全磁化は以下で表される．

式(７)を有理化し，で近似すると，高周波磁化率は

で表される．共鳴吸収スペクトルはの虚部を取って，

となり，ローレンツ関数で表される．ここでローレンツ関数の半値半幅はとなる．したがって，共鳴スペクトルの半値半幅を測定することで，反強磁性磁化ダイナミクスの緩和を示すパラメータであるダンピング定数を求めることができる．

3．THzスペクトロスコピー

　本研究では，連続波及び周波数掃引が可能なTHz技術を用いて分光を行っている．図1に概略を示す．二つの分布帰還形レーザ光源（DFB Laser: Distributed feedBack Laser）を利用して，波長が異なる（及びとする）レーザ光をファイバ型結合器を介して混合する．混合されたレーザ光には，波長差に対応した周波数で強度変調（ビート）が起こる．ここで，は光速．このビートレーザ光を光伝導スイッチ（PCS: photoconductive switch）に導入すると，の周波数でオンオフを繰り返す．ここにバイアス電圧を加えるとPCSに掛かる電界がで振動し，電磁波を放射する（エミッタ：図1左側）．例えば，，とすると，となる．

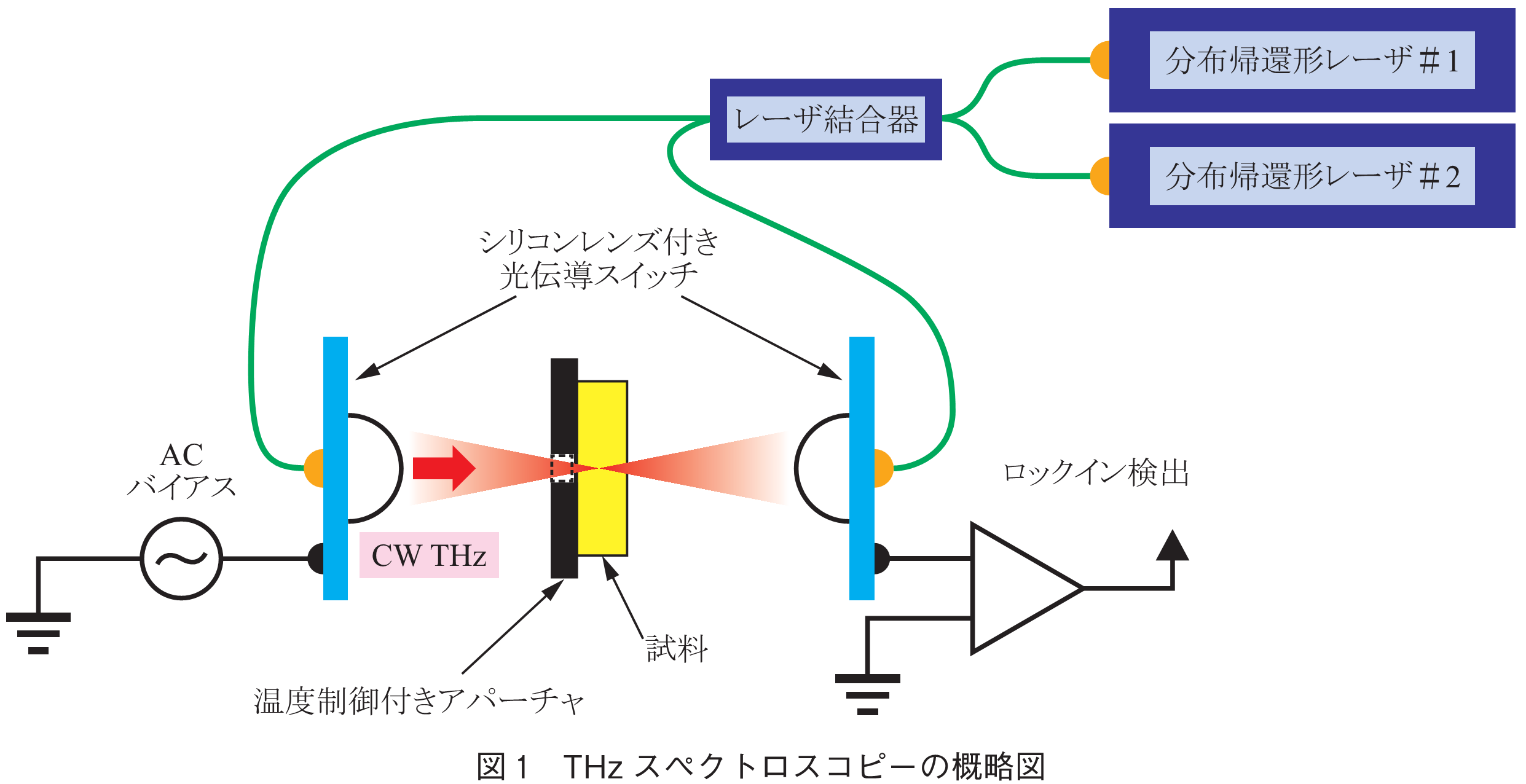
　放射された電磁波はSi球面レンズで試料に集光され，透過電磁波の強度はデテクタ（図1右側）により検出される．デテクタもエミッタと同様にPCSで構成されており，PCS上での電磁波とビートレーザ光のヘテロダイン検波を利用して電流信号として検出する．本実験では波長可変分布帰還形レーザ光源を利用しておりは0～2THzで調整可能であり，電磁波強度は10^－6W程度，周波数精度は10MHz以下である．

4．NiOの反強磁性共鳴及び磁気ダンピング

　典型的なコリニア反強磁性体であるNiOについて，THz分光を行った結果を示す．本実験では，(111)面でへき開したバルク単結晶体（厚さ0.45mm）と，粉末焼結法により得た多結晶体（厚さ1.4mm）の反強磁性共鳴を無磁界下において試料温度（）を変化させて測定し，比較した．図2(a)にX線回折の結果を示す．線幅及びSEMによる試料断面の解析から，多結晶体については結晶粒の大きさは100nmから10µmで分散していることが分かった．これらの試料をにおいて測定したテラヘルツ透過スペクトルを図2(b)に示す．単結晶試料では厚さ方向の多重反射による干渉（ファブリペロー干渉）のせいで周波数に対して透過強度が周期的に振動しているのが見られる（図2(b)上段）．図2(b)中段は，適切なモデルによりこの振動成分を排除したスペクトルである．単結晶試料及び多結晶試料共に1THz付近に鋭い吸収が見られており，先行研究におけるNiOの反強磁性共鳴周波数と良い一致を示している^(9),(10)．

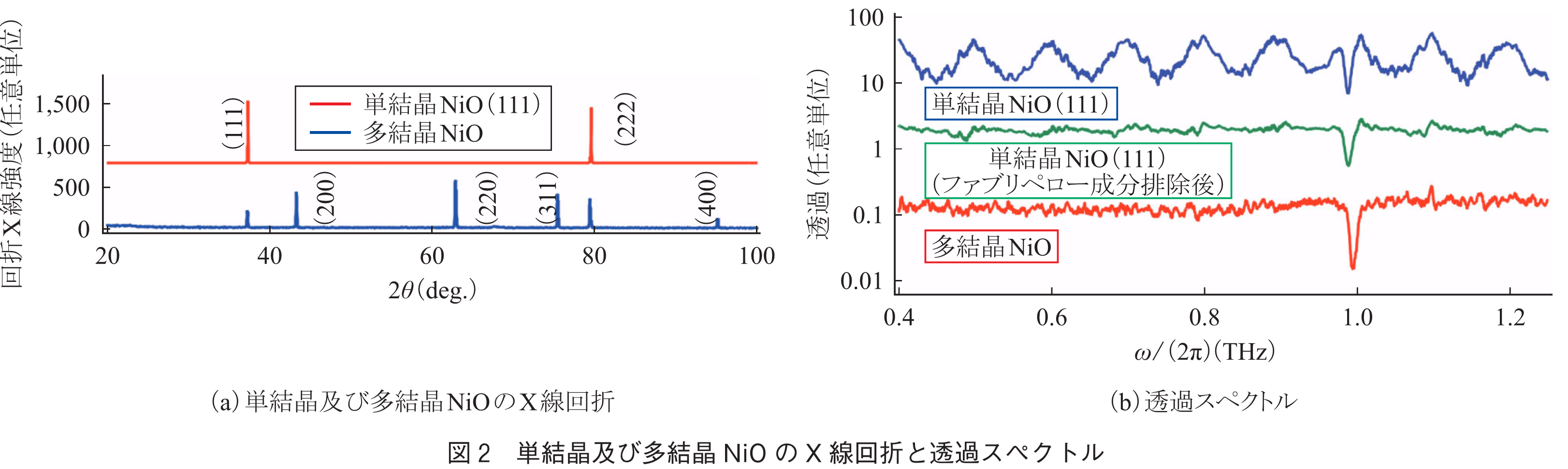
　図3に共鳴周波数及び共鳴線幅（半値半幅）の温度依存性を示す．単結晶及び多結晶どちらの試料においても，共鳴周波数はNiOのネール温度^(用語)（）に向かって急激に減少しているのが分かる．共鳴周波数は，式(６)から，であるが，分子場定数は温度に依存しないので，温度に依存する変数は及びのみと考えられる．異方性エネルギーはのべき乗に比例するので⁽⁸⁾，共鳴周波数の温度依存性はで記述できる．ここで，は0Kにおける共鳴周波数，はでので規格化された副格子磁化である．は，N^2＋のスピン量子数を考慮して，ブリユアン関数から導かれる．として，図3(a)，(b)に得られたデータをフィッティングすると，両試料において，が得られた．これは，分子場近似（）が必ずしも正確でないことを示している⁽¹⁵⁾．に関しても，単結晶及び多結晶ではほとんど差異がない．これらは，分子場定数や副格子磁化，異方性エネルギーがNiOの結晶性にほぼ依存しないことを示唆している．

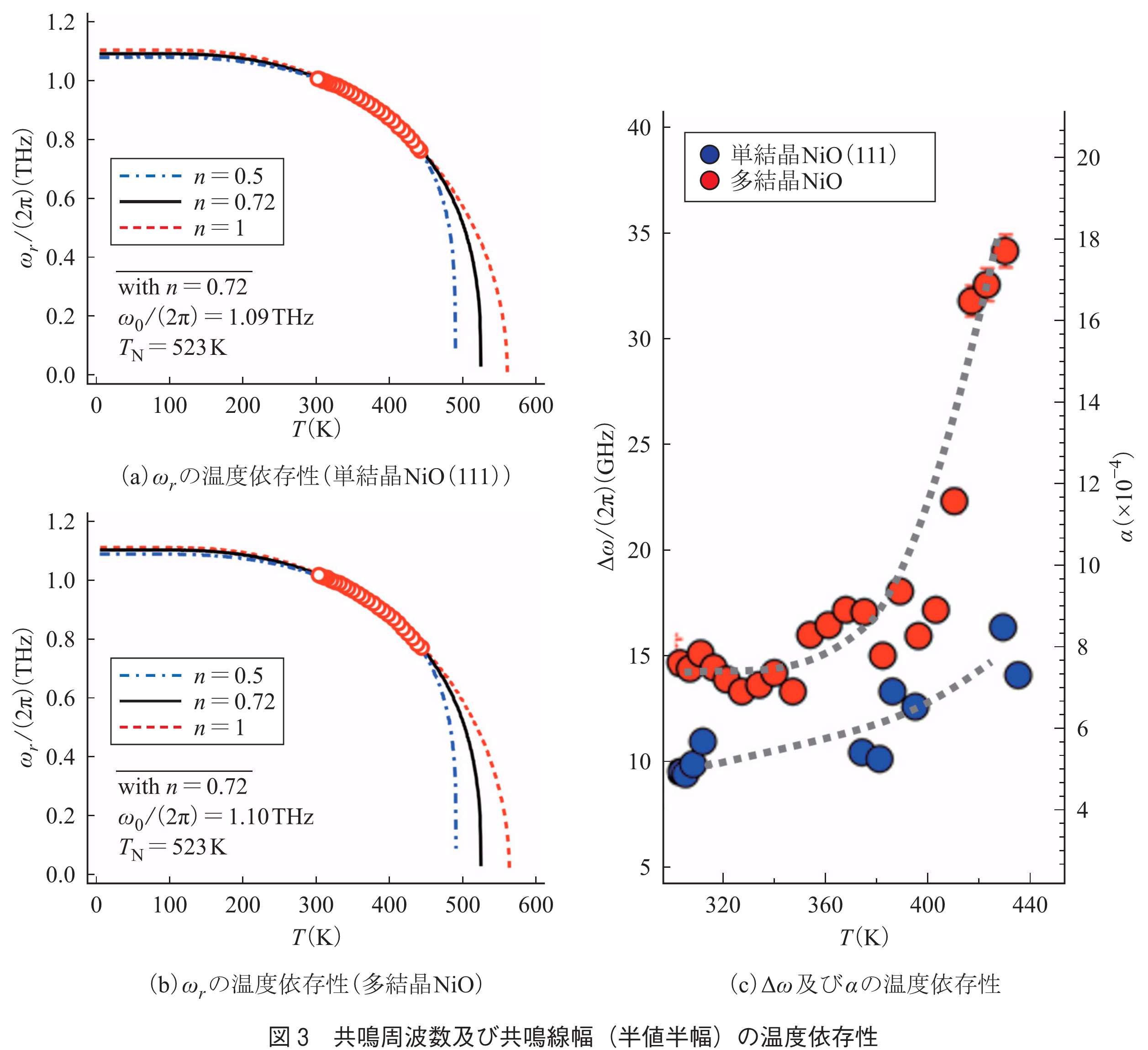
　一方，は多結晶の方が単結晶よりも1.5倍程度大きいことが分かる．において，単結晶のダンピング定数は，多結晶では7.4±0.4×10^－4であった．更に，多結晶のは温度に対してより急しゅんに増加することが分かった．これらの違いは，強磁性体の場合と同様に，反強磁性ダイナミクスにおいても内因性及び外因性の磁気ダンピング^(用語)が存在することを示唆している．

5．元素置換による共鳴周波数及びダンピング制御

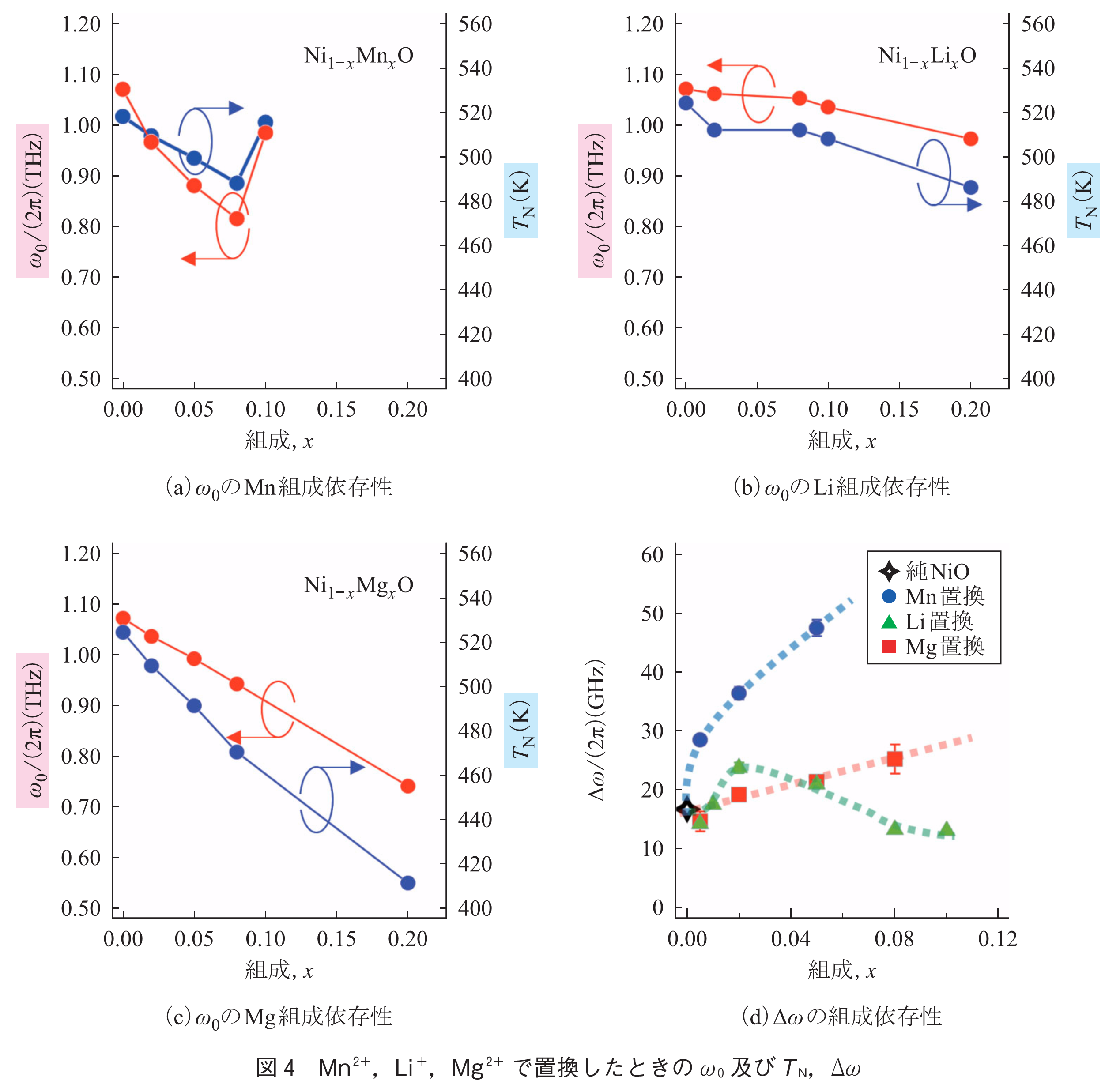
　反強磁性共鳴周波数は，分子場定数や副格子磁化，異方性エネルギーに依存する．これらは，Ni^2＋カチオンを種々のカチオンで置換することで変化させることができる．図4は磁性イオンであるMn^2＋，非磁性イオンのLi^＋，Mg^2＋で置換したときの及び，である．Mn 10%置換の試料以外は全て母相NiOの結晶構造を保ちつつカチオン置換されていることをX線回折において確認している．Mnで置換した場合，置換量に対しての方がよりも大きく減少していることが分かる．ここで，交換磁界を異方性磁界とすると，は交換磁界と異方性磁界の積の平方根に比例する（式(６)）．は交換磁界に比例すると考えると⁽¹⁶⁾，との減少率から，Mn置換は，主に異方性磁界を減少させることが分かった．一方MgやLiで置換した場合は，との減少率から異方性磁界と交換磁界両方にほぼ同等に作用することが分かった．これらは，交換相互作用が非磁性イオンで阻害されるのに対して，磁性イオンではそれほど影響がないということで説明できる．カチオン置換によるの制御性はMn置換で最も大きくで，次にMg置換で，Li置換で最も小さくであった．

6．反強磁性ダイナミクスによるスピンポンピング

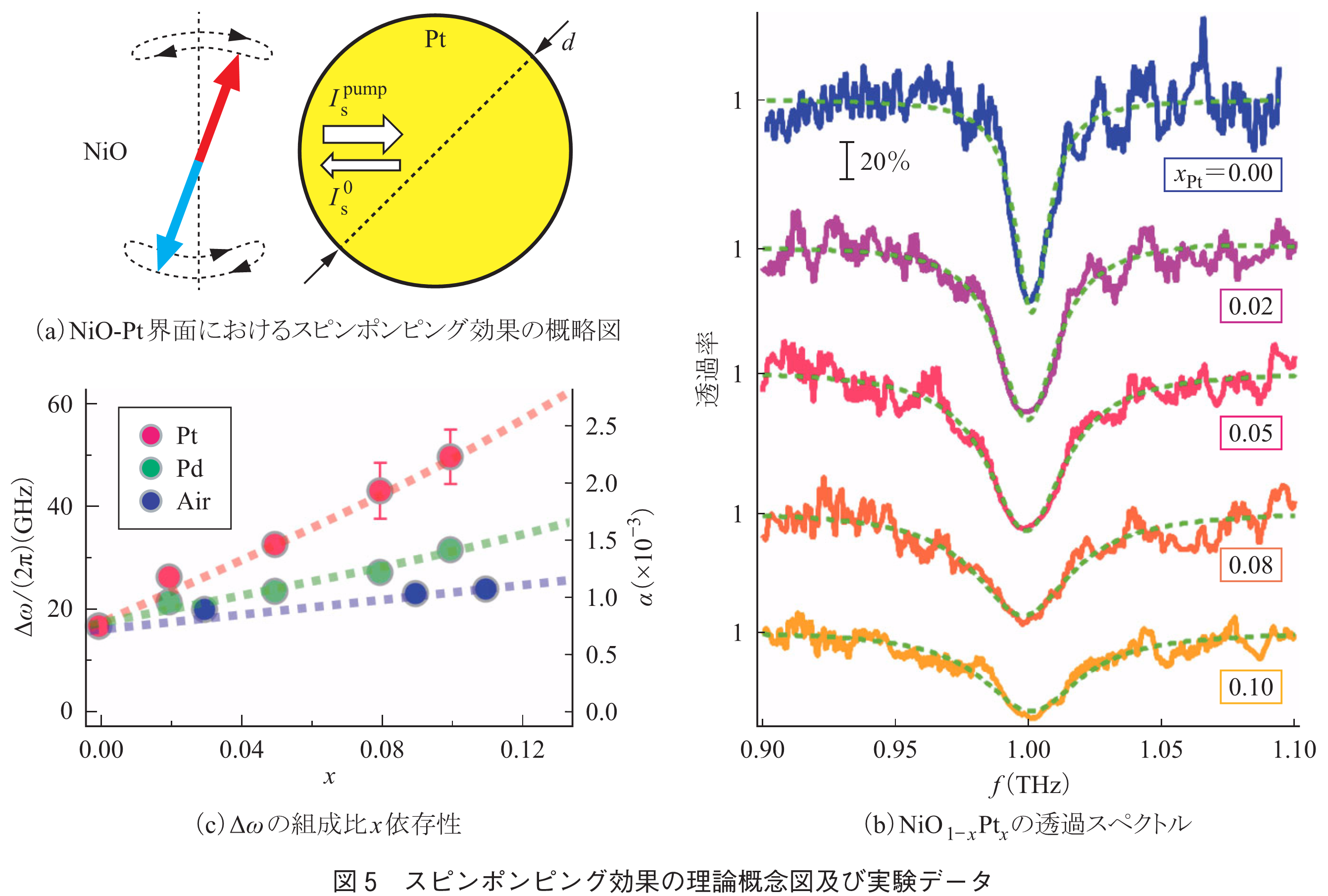
　磁化ダイナミクスに付随する興味深い現象としてスピンポンピング効果がある．スピンポンピング効果は磁化方向の時間変化がスピン流に変換される現象で，強磁性体においてはよく知られた現象⁽¹⁷⁾であるが，THz帯域の反強磁性磁化ダイナミクスにおいて観測された例はほとんどない．本研究では，NiO-Ptグラニュラー物質^(用語)において反強磁性ダイナミクスによるスピンポンピング効果について調査した．NiO中にPt粒子を様々な割合で分散させたグラニュラー物質（）に対してテラヘルツ透過吸収測定を行った．この試料系におけるスピンポンピング効果の理論概念図を図5(a)に示す．NiOの反強磁性磁化ダイナミクスにより，スピン流が生成され，Pt粒子に注入されスピン蓄積が起こる．Ptはスピン軌道相互作用が強いためのほとんどは散逸し，残った僅かなスピン蓄積によりスピン流の逆流が起こる．反強磁性磁化ダイナミクスのダンピング定数は，との差，すなわち重金属でのスピン散逸の大きさに比例して増加することが理論的に知られている．つまり，グラニュラー物質中のPtの割合を増加させてスピン散逸が増加するに従いNiOの磁化ダイナミクスのダンピング定数は大きくなることが予想できる．強磁性共鳴の場合と同様，反強磁性磁化ダイナミクスのダンピング定数は，反強磁性共鳴のスペクトル線幅から見積もることができる．テラヘルツ透過吸収測定から得られたの透過スペクトル（図5(b)）はちょうど1THzに共鳴ピークを示している．更に，共鳴周波数はPtの組成比によらず一定であるのに対して，共鳴線幅はの増加に従って大きくなっていることが分かる．これは，スピンポンピング効果の理論予想と一致しており，THz帯の反強磁性スピンダイナミクスにおいてもスピンポンピング効果が起こることを実証している．更に，これらのデータから，スピンポンピング効果の多寡を決定するパラメータであるスピンミクシングコンダクタンスはNiO/Ptにおいて12nm^－2と見積もられた．また，Pd粒子についても同様の測定を行ったところ，NiO/Pdにおけるスピンミクシングコンダクタンスは5nm^－2と見積もられた．これらは，強磁性体におけるスピンポンピング効果と同程度の値であり，反強磁性体においても比較的大きなスピンポンピング効果が得られることが明らかになった．

7．ま　　と　　め

　典型的なコリニア反強磁性体であるNiOの反強磁性共鳴を中心に，ダンピング定数の調査や，共鳴周波数の制御，スピンポンピング効果について紹介した．THz測定技術の発展により，反強磁性ダイナミクスやダンピング定数が詳細に調査できるようになってきた．テラヘルツ応用において共鳴周波数やQ値の制御は重要である．また，反強磁性体において比較的大きなスピンポンピング効果が発現することを示した．最新の報告では反強磁性ダイナミクスによるスピン起電力の検出⁽¹⁸⁾など，スピンポンピング効果を発展させた興味深い研究が継続して成されている．このようなTHz帯域での磁化ダイナミクスとスピン流との相互作用は，反強磁性体でしか成し得ない独特の現象である．スピントロニクス分野とテラヘルツ分野を融合する重要な材料としての反強磁性体に期待したい．

　謝辞　本研究は多くの研究者との共同研究の成果である．共同研究者の皆様に感謝する．本研究は，科研費特別推進研究15H05702，基盤研究（S）20H05665，基盤研究（A）21H04562，挑戦的萌芽19K21972，JST-さきがけJPMJPR20B9の助成を受けて行われた．

文　　　　　献

（2022年6月29日受付　2022年7月26日最終受付）