1．機械学習の公平性とは

　機械学習技術は普及し，入学，就職，与信などの，個人の生活に大きな影響を与える決定にも利用されるようになってきた．そのため，その予測は様々な社会的要請に応える必要が生じたが，ここでは特に公平性について取り上げる．

　差別“discrimination”という語は，商品の差別化などのように常に悪い意味で使われるわけではない．Lippert-Rasmussenのまとめ⁽¹⁾によれば，どのような差別が悪いものとなるかについて有力な二つの学説がある．一つは，害ベース説（Harm-based Account）で，被差別者がより不利に扱うことで悪くなり，もう一つの尊厳ベース説（Disrespect-based Account）は非差別者を道徳的に軽んじることで悪くなるというものである．害ベース説では，誰かを有利に扱うとその他の人は不利になるのに対し，尊厳ベース説では，誰かを賞賛しても必ずしもその他の人を侮蔑しているとは限らないという対称性などの相違点がある．機械学習の公平性では，次の二つの理由により前者を扱う．まず，尊厳ベース説では，定量的評価自体を否定する考えもあり，この考えでは統計的手法や機械学習は否定される．一方で，米国の司法では害ベース説に基づく判断があり，それらの判断に応えるべく機械学習の公平性技術は開発された．

　このまとめでは更に害ベース説において，何に対して不利に扱われているかの二つの基準を示している．本来あるべき理想的な状態を基準とするもので，これに対して連関ベース公平性が開発された．一方で，もしも被差別者が差別されていなかったらどうなったかを基準とするもので，これに対しては反実仮想公平性が対応する．これらを順に紹介する．

2．連関ベース公平性

　連関ベースの公平性（Association-based Fairness）は，近年では統計的独立性に基づいて理想的に公平な状態を定める．まず，説明に必要な変数を定める．センシティブ特徴（Sensitive Feature） math は，公平性を保証する性質を表し，非センシティブ特徴（Non-sensitive Feature） math はセンシティブ特徴以外の全てを含む特徴ベクトルである．確率変数 math は目的変数で，何らかの決定を表し，更に結果の予測値を math と，観測値を math として区別する．例えば，与信，採用，保険などの決定を math で表すとき，社会的公平性の観点からその関与を排除すべき対象者の性別や人種といった情報を math で表す．

　無視による公平性（Fairness through Unawareness）から説明する．これはセンシティブ特徴を予測モデルで用いないことで達成されるもので，センシティブな情報を収集しないという意味でのプライバシー制約をも満たす．予測モデル math が math を使わないことで math に等しくなることを用いれば，条件付独立性 math が容易に示せる．全ての変数が2値である場合を図1（a）に示した．この図から，縦に math か1で分割したあと，この各分割において math と1の間で math の比率が一致する条件であるということが分かる． math は，採用におけるスキルや与信における経済状況など，性別や人種などのセンシティブ情報とは直接的には無関係な特徴を表しているので，これらが同じ人の間ではセンシティブ情報に関わりなく同じ割合で採用されたり，借金できたりするということである．これはすなわち，同一スキルや状況の個人間での公平性である個人公平性（Individual Fairness）が同時に保たれているということでもある．

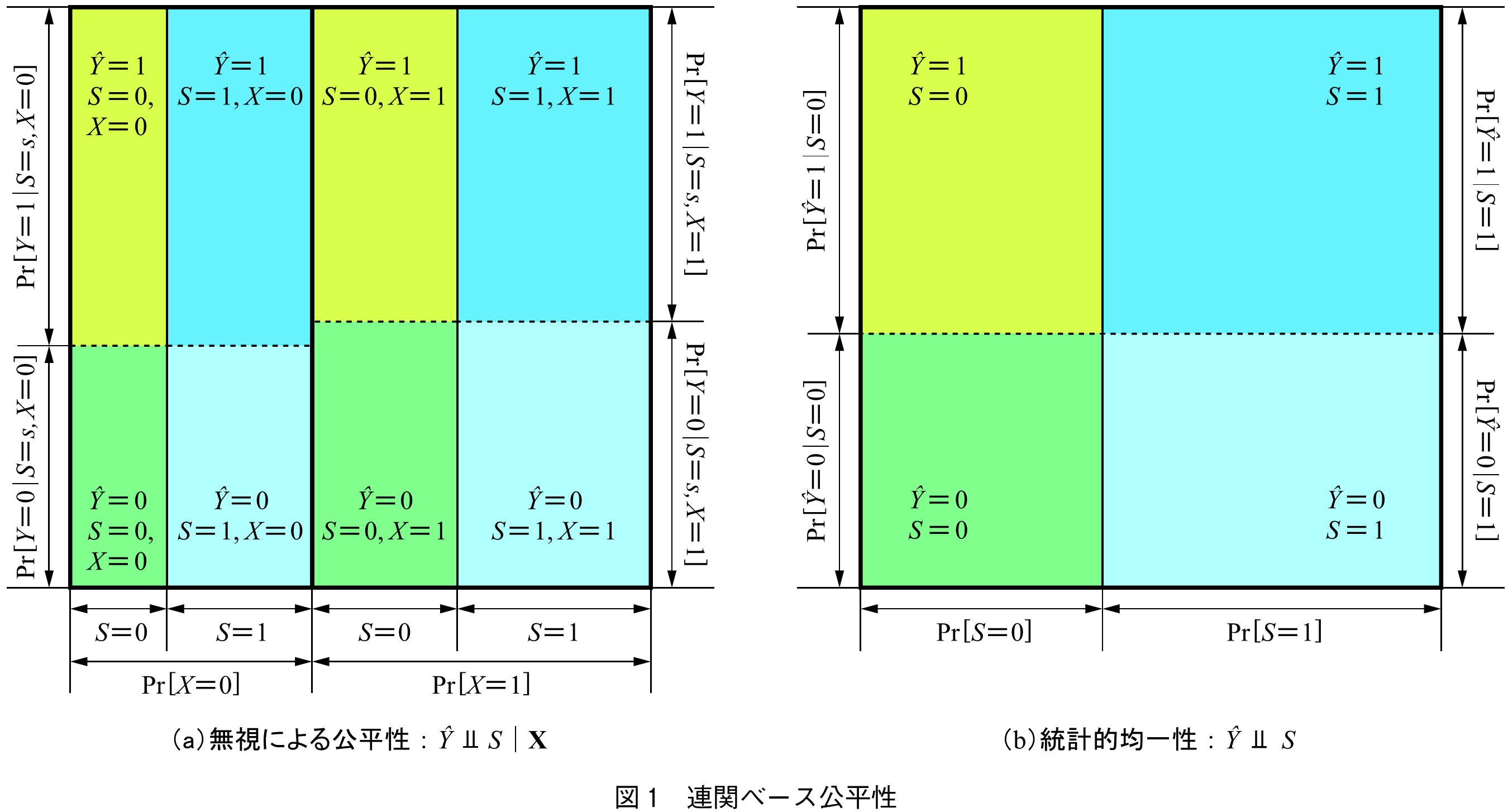
　次の統計的均一性（Statistical Parity）は，米国の判例Hazelwood School District v. United States⁽²⁾で示されたGross Statistical Parityに対応するものである．これは，条件なしの独立性 math にあたり，図1（b）のように，センシティブなグループ間で math となる割合が等しいという条件である．無視による公平性は直接差別は除去できるが， math を通じて math の情報が math に影響する間接差別には対応できないというRed-lining効果がある．一方で，統計的均一性は間接差別は間接差別をも取り除くが，必ずセンシティブ情報を参照して補正する必要があるので，プライバシー保護は達成できない．

　統計的均一性は，過去のデータ中の判断 math は不公平な判断に基づくものとし，それらを修正する積極的格差是正措置を伴う．それに対しデータ中の math は公平とみなす公平性に，十分性（Sufficiency）や均等オッズ（Equalized Odds）がある．これらは，有限個のデータ一般化して予測をするときに必要となる仮定から生じる帰納バイアスが元になった不公平を取り除く．十分性は math であり，与えられた予測値 math が実際にそのとおりになる割合がセンシティブなグループ間で等しいというものである．そのため，予測値 math を目安や物差しとして用いるときに適切で，教育や心理の指標の公平性として用いられてきた．もう一つの均等オッズ math では，広く用いられている誤差指標である偽正率や偽負率が等しくなるようにする．

　以上，4種類の公平性を示したが，無視による公平性と均等オッズの組以外は，同時に満たすことは数理的不可能問題であり，人間であっても不可能となり，社会が選択する必要がある点は重要である．

3．反実仮想公平性

　反実仮想公平性（Counterfactual Fairness）は，現状の math の値では math はこうだが，もし仮に math を違う値に変えたとしても math の値が変わらないのであれば公平であるとする．これは米国の判例Jack Gross, Petitioner, v. FBL Financial Services⁽³⁾で示されたBut-for Causeに基づく考えに対応している．この考えは，既に math の値を知った状態でもしも math の値を変えたらという後ろ向きに振り返ったときの介入効果を考えるという，因果推論における十分性の確率に該当する． math はそのままで math の値が異なる点では個人公平性と似ているが， math の値だけが異なる場合を集めた場合を観察する個人公平性に対し， math の値を介入によって変える点が重要な相違である．

3.1　社会との関連

　機械学習の公平性に関して，ProPublicaの問題提起とAI関連の法・規則について述べたい．データ分析を用いたエビデンスに基づくジャーナリズムであるデータジャーナリズムNPOのProPublicaによる再犯リスクスコアCOMPASに対する指摘を紹介する⁽⁴⁾．COMPASは，被告人が2年以内に再び犯罪を犯す可能性を評価するもので，過去の裁判システムには人種に対する主観的な偏見があったとの反省に立ち，エビデンスに基づく決定を重視するという方針で導入が進んでいる．ProPublicaは，このCOMPASが均等オッズを満たさず不公平であると指摘した．それに対し裁判所は反論⁽⁵⁾し，五つの重大な問題点を指摘している．そのうちの一つは，該当分野の標準に基づき十分性を満たすよう設計されているため，均等オッズを同時に満たすのは数理的に不可能であるという主張である．更に，判事と比較するとはるかに公平かつ正確であり⁽⁶⁾，司法の公平性の改善に大きく寄与していると述べている．各種の公平性規準は同時には満たせないため，このCOMPASの例に倣い，どの規準を採用したのかを公表することは重要である．

　執筆時（2024年8月）では，EUのAI Act⁽⁷⁾，米国の大統領令⁽⁸⁾，日本のAI事業者ガイドライン⁽⁹⁾などのAI関連の法令・規定が示されているが，技術的には不明瞭な点があると筆者は考えている．いずれでも，公平性とプライバシーの両立を要求しているが，上記のようにセンシティブ情報を秘匿するというプライバシーとほとんどの公平性規準を両立させることは数理的不可能問題である．こうした不可能性のほかに，必要となるであろう判断が行われていない問題もある．学習データの偏りがないことをいずれでも要求しているが，これは統計学における標本選択バイアス問題にあたり，その補正技術は1979年以降広く研究されている．しかしながら，偏りのない状態について判断がなされていないため，これらの技術を適用できていない．例えば，入試では，受験者，学校のある地域，国全体で人種の分布などからいずれが偏りのない状態を選択する必要がある．