
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

複雑コミュニケーションサイエンス研究専門委員会
揺らぎ
揺らぎは電子システムや自然界にあまねく見られ,成因は多種多様である.揺らぎの意味としては,注目している量の平均値の近傍での動的なずれであるが,電子情報通信分野では多くの場合雑音と重複するであろう.揺らぎに関係する事象を図1に示す.明確な区分や規則はないが,時間スケールによっておよそ区別される.揺らぎの語感はふらつきに近いが,広義の揺らぎは図1に示すように広い範囲を包含する.
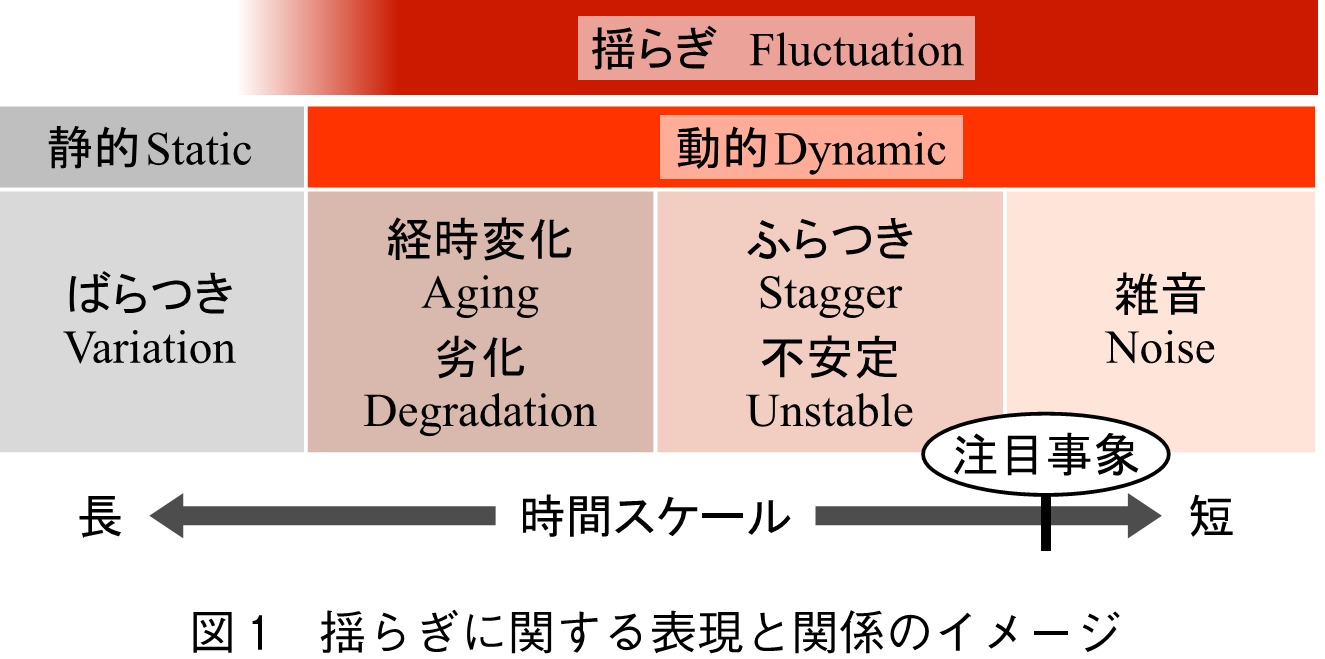
揺らぎが注目される背景として,機器の低消費電力化や情報伝送の高速化がある.いずれもSN比(信号と雑音のパワーの比)の劣化を伴う.計測機器の発達も揺らぎを身近にした.長い時間スケールの事象を十分短い時間ステップでかつ高い垂直分解能で捕捉可能になり,揺らぎを正確に捉え議論できるようになったと言える.
揺らぎの特徴を表すパラメータを知ることでより良い信号計測や議論が可能になる.
周波数スペクトルの縦軸をパワー密度(PSD : Power Spectral Density)としたとき,着目する周波数帯におけるスペクトルの傾きで揺らぎ(雑音)を区別し「色」で表現する(図2).信号よりも十分広い帯域でスペクトルがフラットである場合白色雑音と呼んでいる.自然界にある揺らぎはピンク雑音である.ブラウニアン雑音とブラウン雑音は区別があり,前者はブラウン運動によって生成される揺らぎで,後者はスペクトルが
の揺らぎである.ただし,結果的にこれらは同一である(1).
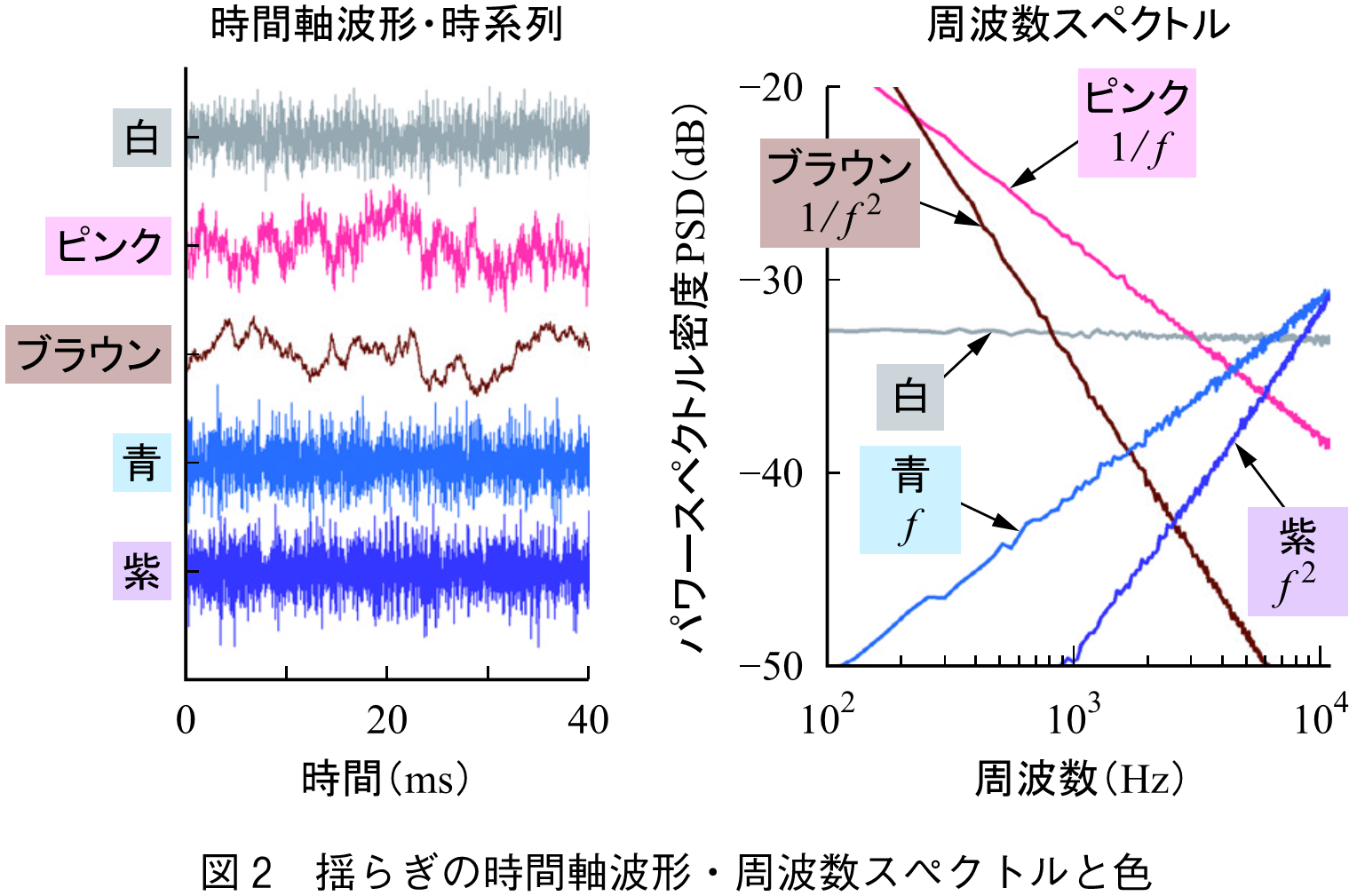
周波数スペクトルに特定のピークが観測されなければ時間軸波形には周期性はなく,不規則(ランダム)と考えられる.ただしインパルス波の可能性もあり,波形の確認が必要である.
揺らぎ源が複数あるとき,相互の類似性を相関係数で評価する.また揺らぎの波形に何らかの周期構造が見られるときは自己相関を用いる(図3).自己相関は時間(位相)をシフトさせつつ原波形との相関係数を評価する.自己相関が0に至るまでのシフト量を自己相関時間と言い,波形が不規則であれば自己相関時間は短くなる.ただし逆は真ではない.例えば,長周期のインパルス列はパルス幅に相当する時間で自己相関が0になるが周期性は存在する.
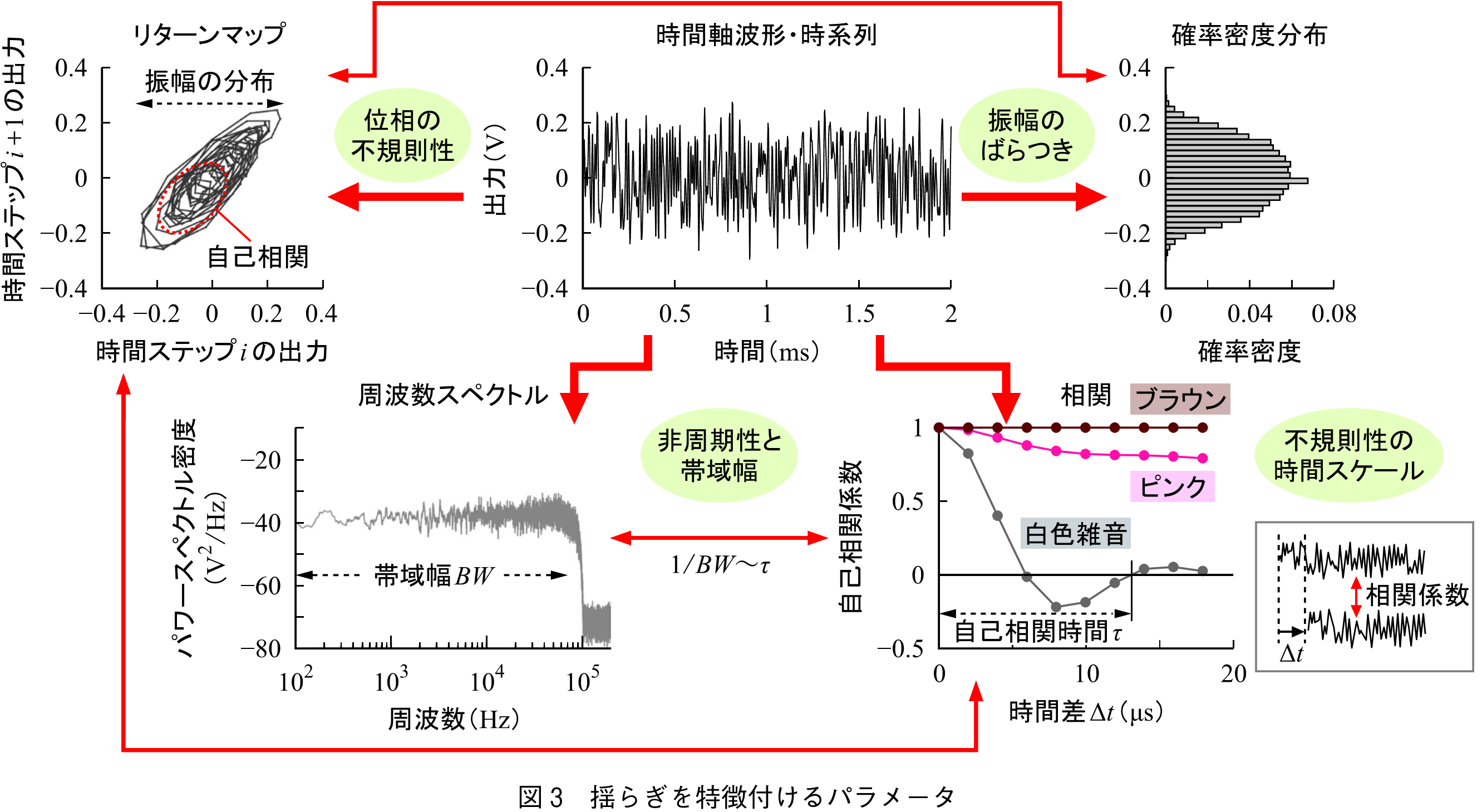
離散的な時系列であればランダム性を視覚的に確認する手段としてリターンマップ(位相プロット,ポアンカレプロット)がある.ランダムかカオスであるかの区別がつく(2).
確率密度は振幅(位相揺らぎの場合は位相)をパラメータとし各振幅値が出現する確率を表したものであり,振幅のばらつきを表現する.確率密度がガウス分布のときガウス雑音(Gaussian Noise)と呼ぶ.確率密度分布は確率ダイナミクスの解析に不可欠である.一般的に,自然界に多くかつ数学的に扱いやすいガウス分布を仮定することが多い.複数の白色ガウス雑音を加算した加法性白色ガウス雑音(AWGN : Additive White Gaussian Noise)もよく用いられる.なお白色スペクトルとガウス性は独立した性質である.
揺らぎは生物にとって多様性,適応能力,探索能力の源泉であり,生存のために不可欠である(3), (4).揺らぎが能動的に働いている生体機能・自然現象の例を幾つか示す.
確率共鳴とは,揺らぎによって微弱信号に対する感度が高まる反直感的な非線形現象である(5).最初の指摘は地球の氷河期の周期的到来のモデルである(6).その後,ザリガニ(7)など生物の感覚機能において現象が相次いで確認され,現在は生物機能の一つとして知られている.その基本機序は,しきい値系や双安定系のような非線形系における雑音支援による状態遷移である.確率共鳴は生物・自然界にとどまらず人工的な非線形系でも発現し,単電子系(8)や分子系(9)のような極微細な系でも観測される.現象を説明する数理モデルが多数報告されているが,反直感性を明快に説明するものはこれまでなかった.最近,雑音の分布関数の非線形性に反直感性の起源があることが指摘された(10).
ブラウンラチェットはブラウン運動から方向性の運動・流れを取り出す機構で,生物の力学的運動を担う分子モータの駆動源である.開放系において機能するものであり,断熱系における熱力学的第2法則には抵触しない.分子モータでは長いレール状のミオシン分子の上をアクチンが熱揺らぎによって一次元方向にランダムに移動している.ATP(アデノシン三りん酸)がアクチン分子に作用すると一方向の動作のみをロックし(ラチェット),熱揺らぎから方向性の運動が取り出される(11).この状況は可動粒子を携えた周期的非対称ポテンシャルの消滅・形成の反復(フラッシング),あるいは全体を揺りかごのように揺する(ロッキング)ことで再現される(12).ナノテクノロジーの発展によりランダムに動く電子から一方向電流を生成するブラウンラチェット素子のデモが可能になった(13)~(15).
生物が過酷な環境で生き残るために欠かせない探索能力や適応能力に揺らぎが関与している.探索を物理系に当てはめると,複雑なポテンシャルランドスケープ下でのエネルギー最小状態への状態遷移となる.遷移の過程でしばしばエネルギー極小状態に陥るが,揺らぎが脱出を可能にする.このような状態遷移過程はイジングマシンと呼ばれるコンピュータの計算過程そのものである.本計算では系に積極的に揺らぎを加える擬似アニーリング(SA : Simulated Annealing)が有効であるが,その背景にはエルゴード仮説がある(16), (17).自然環境ではポテンシャルランドスケープそのものが動的に変化し,エネルギー最小位置も時間とともに変わり得る.動的な環境変化に動的に追従するにも揺らぎが不可欠である.
(1) 小山順二,原 啓明,“ランジュバン方程式のスケール変換によるブラウン運動の一般化とそのスペクトル構造,”統計数理,vol.40, pp.17-26, 1992.
(2) C. Oestreicher, “A history of chaos theory,” Dialogues in Clinical Neuroscience, vol.9, pp.279-289, 2007.
(3) A.A. Faisal, L.P.J. Selen, and D.M. Wolpert, “Noise in the nervous system,” Nature Rev. Neurosci., vol.9, pp.292-303, 2008.
(4) C.V. Rao, D.M. Wolf, and A.P. Arkin, “Control, exploitation and tolerance of intracellular noise,” Nature, vol.420, pp.231-237, 2002.
(5) L. Gammaitoni, P. Hänggi, P. Jung, and F. Marchesoni, “Stochastic resonance,” Rev. Mod. Phys., vol.70, pp.223-287, 1998.
(6) R. Benzi, A. Sutera, and A. Vulpiani, “The mechanism of stochastic resonance,” J. Phys. A, vol.14, pp. L453-L457, 1981.
(7) J.K. Douglass, L. Wilkens, E. Pantazelou, and F. Moss, “Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance,” Nature, vol.365, pp.337-340, 1993.
(8) S. Kasai, “Thermally driven single-electron stochastic resonance,” Nanotechnology, vol.33, p.505203, 2022.
(9) Y. Hirano, Y. Segawa, T. Kawai, and T. Matsumoto, “Stochastic resonance in a molecular redox circuit,” J. Phys. Chem. C, vol.117, pp.140-145, 2013.
(10) S. Kasai, A. Ichiki, and Y. Tadokoro, “Divergence of relative difference in Gaussian distribution function and stochastic resonance in a bistable system with frictionless state transition,” Appl. Phys. Express, vol.11, p.037301, 2018.
(11) H. Tanaka, et al., “The motor domain determines the large step of myosin-V,” Nature, vol.415, pp.192-195, 2002.
(12) R.D. Astumian, “Thermodynamics and kinetics of a brownian motor,” Science, vol.276, pp.917-922, 1997.
(13) H. Linke, et al., “Experimental tunneling ratchets,” Science, vol.286, p.2314, 1999.
(14) E.M. Roeling, et al., “Organic electronic ratchets doing work,” Nature Mat., vol.10, pp.51-55, 2011.
(15) T. Tanaka, Y. Nakano, and S. Kasai, “Fabrication and characterization of GaAs-based nanowire devices having multiple asymmetric gates for electrical brownian ratchet,” Jpn. J. Appl. Phys., vol.52, p.06GE07, 2013.
(16) 西森秀稔,新物理学選書スピングラス理論と情報統計力学,岩波書店,2016.
(17) 後藤隼人,“シミュレーテッド分岐マシンの原理と応用,”表面と真空,vol.63, pp.129-133, 2020.
(2024年2月25日受付)
オープンアクセス以外の記事を読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード