
|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

|
電子情報通信学会 - IEICE会誌 試し読みサイト
© Copyright IEICE. All rights reserved.
|

マイクロ波研究専門委員会
変換電磁気学
変換電磁気学とは,座標変換をマクスウェル方程式の構成関係式への操作と捉え,座標変換と等価な異方性媒質を構成することで,電磁波や光の伝搬を操る概念である.変換光学とも呼ばれる.
20世紀の初頭に相対論(1)が提案されて以降,一般の座標系におけるマクスウェル方程式は広く取り扱われている(2),(3)が,2006年にPendryらは,マクスウェル方程式において,座標変換に伴う演算子やベクトルへの操作を誘電率テンソル及び透磁率テンソルに組み込むことによって,方程式の形式が保存され,媒質中の電磁波が変換を受けた座標系に従い伝搬することを示した(4).これが変換電磁気学における電磁波伝搬操作の概念であり,座標変換の媒質的解釈とも呼ばれる.また,座標変換が組み込まれた媒質は,座標変換媒質あるいは変換媒質と呼ばれている.
座標変換媒質は,変換前の空間と等価となる.変換前の空間が均質な媒質で満たされているとすれば,任意の座標変換に対して,電磁波は座標変換媒質中で反射・散乱なく伝搬する.また,媒質境界を座標変換の前後で外部と連続にとれば,境界において電磁波は整合し,反射しない.この性質を用いて,覆うと物体が不可視となる透明マント(4),(5)や,反射形の透明マントであるカーペットクローク(6)が構成される.また,本概念を用いて,存在しない物体があたかもあるかのように見えるイリュージョン媒質(7)も構成可能である.
座標変換媒質は,誘電率と透磁率の同時操作が可能なメタマテリアルを用いて実装される.これまで,SRR(split-ring resonator)を用いたもの(5),誘電体を用いたもの(8),(9),伝送線路理論に基づくもの(10)などの実装法が提案されている.また,方解石など自然の一軸性結晶による実装法も提案されている(11).
比誘電率テンソル及び比透磁率テンソル
の媒質で満たされた空間を,座標
から座標
に変換する座標変換媒質の比誘電率テンソル
及び比透磁率テンソル
はそれぞれ次式で与えられる(4).
(1)
(2)
ここで,はヤコビ行列
であり,上付きのTは転置,detは行列式を表す.
元の座標系が,比誘電率及び比透磁率
の均質な媒質であるとき,式(1)及び式(2)は,計量テンソル
(
は基底ベクトル)を用いて,
(3)
(4)
と表わされる.式(3)及び(4)から,変換後の基底が直交するとき,及び
の非対角項が0となる性質があることが分かる.また,変換前後で微小体積要素が変化しない座標変換では,ヤコビ行列の要素が1となり,誘電率及び透磁率の絶対値の制御が不要となる.これらは実装上有利となる性質であり,このため,擬等角写像が用いられる(8).
なお,この座標変換により,電界,磁界
,電束密度
,磁束密度
,電流密度
及び電荷密度
は,それぞれ以下に変換される(12).
(5)
(6)
(7)
(8)
(9)
(10)
ここでプライム付きの量は,座標変換媒質中の量を表している.
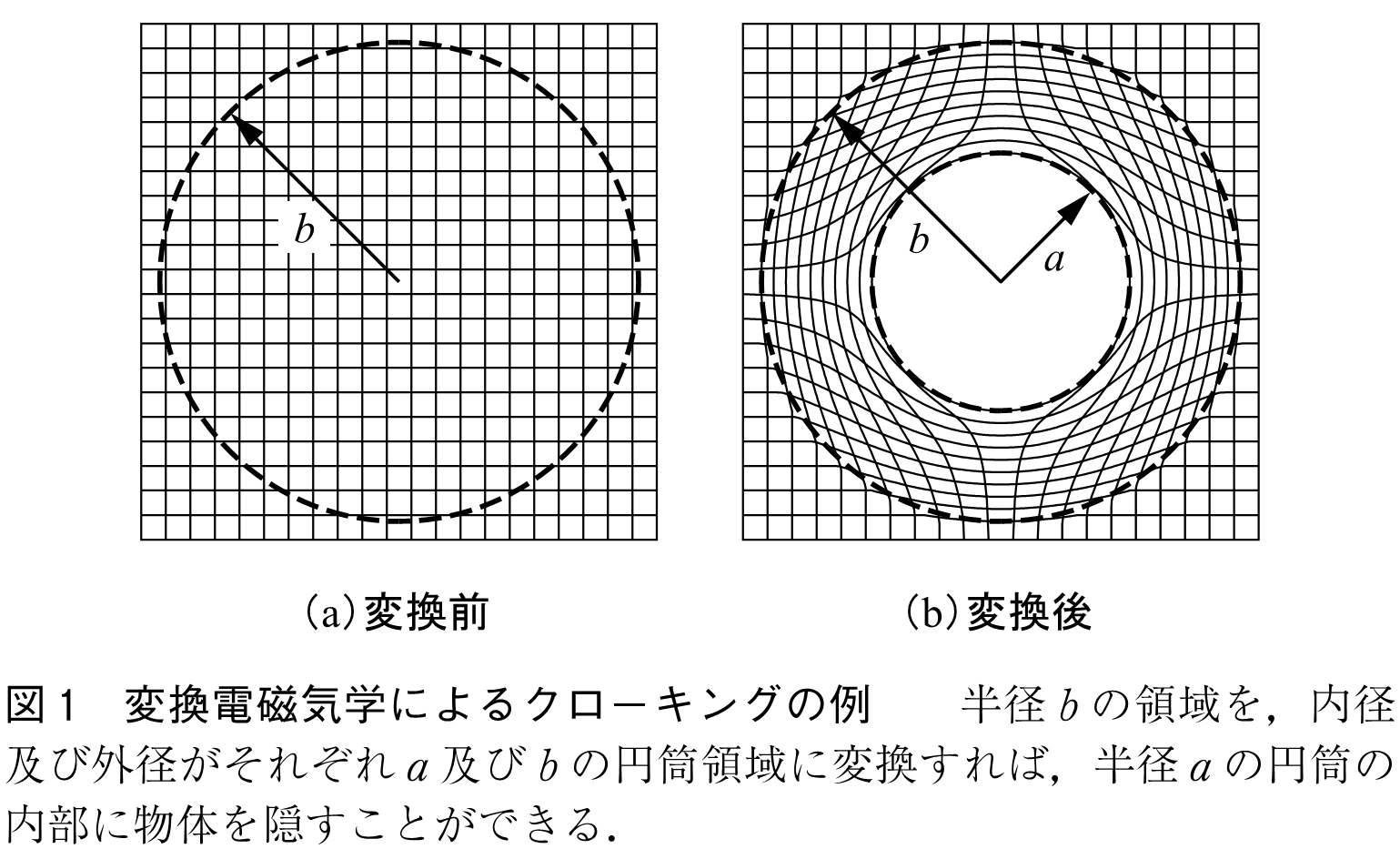
マイクロ波帯におけるSmithらの最初の実証実験(5)における円筒クロークの媒質構成例を示そう.円柱座標系において,図1のような,半径
の領域を,内径及び外径がそれぞれ
及び
の円筒領域に線形に変換する座標変換を考える.すなわち,半径
の内側の領域を
(11)
に変換する.ここで,プライム付きの座標が変換後の座標である.なお,この座標変換は,の境界において変換前後で連続である.これを等価な座標変換媒質で実現すると,電磁波は,円筒の内部にある物体に反射も散乱もされることなく,
の領域をう回して伝搬し,この領域に物体を隠すことができる.この座標変換媒質の比誘電率テンソル及び比透磁率テンソルは,式(11)の座標変換を考慮すれば,式(1)及び(2)から次式のようになる.
(12)
(13)
(14)
ちなみに,この実験(5)では,実際には,偏波の入射波を考慮し,かつアイコナール近似を用い,同じ分散性を持つ次式の媒質が用いられた.
(15)
(16)
(17)
(1) A. Einstein, “Zur elektrodynamik bewegter körper,” Annalen der Physik, vol.322, no.10, pp.891-921, 1905.
(2) E.J. Post, Formal Structure of electromagnetics, general covariance and electromagnetics, North Holland Publishing Company, Amsterdam, 1962.
(3) J.A. Stratton, Electromagnetic theory, John Wiley & Sons, New York, 1941.
(4) J.B. Pendry, D. Schurig, and D.R. Smith, “Controlling electromagnetic fields,” Science, vol.312, no.5781, pp.1780-1782, 2006.
(5) D. Schurig, J.J. Mock, B.J. Justice, S.A. Cummer, J.B. Pendry, A.F. Starr, and D.R. Smith, “Metamaterial electromagnetic cloak at microwave frequencies,” Science, vol.314, no.5801, pp.977-980, 2006.
(6) J. Li and J.B. Pendry, “Hiding under the carpet : A new strategy for cloaking,” Phys. Rev. Lett., vol.101, p.203901, 2008.
(7) T. Nagayama and A. Sanada, “Broadband transmission-Line illusions based on transformation electromagnetics,” EPJ Applied Metamaterials, vol.6, no.23, pp.1-10, 2019.
(8) J. Valentine, J. Li, T. Zentgraf, G. Bartal, and X. Zhang, “An optical cloak made of dielectrics,” Nat. Mater., vol.8, no.7, pp.568-571, 2009.
(9) Y. Maegawa, Y. Nakata, and A. Sanada, “All-dielectric carpet cloaks with three-dimensional anisotropy control,” Nanophotonics, vol.12, no.13, pp.2623-2636, 2023.
(10) T. Nagayama and A. Sanada, “Planar distributed full-tensor anisotropic metamaterials for transformation electromagnetics,” IEEE Trans. Microwave Theory Tech., vol.63, no.12, pp.3851-3861, 2015.
(11) B. Zhang, Y. Luo, X. Liu, and G. Barbastathis, “Macroscopic invisibility cloak for visible light,” Phys. Rev. Lett., vol.106, no.033901, 2011.
(12) G.W. Milton, M. Briane, and J.R. Willis, “On cloaking for elasticity and physical equations with a transformation invariant form,” New J. Phys. vol.8, no.248, pp.1-20, 2006.
(2025年1月14日受付)
オープンアクセス以外の記事を読みたい方は、以下のリンクより電子情報通信学会の学会誌の購読もしくは学会に入会登録することで読めるようになります。 また、会員になると豊富な豪華特典が付いてきます。
電子情報通信学会 - IEICE会誌はモバイルでお読みいただけます。
電子情報通信学会 - IEICE会誌アプリをダウンロード