1．トポロジカルフォトニクスとは

　トポロジカルフォトニクスとは，物性物理学におけるトポロジカル相の発見に触発されて興ったフォトニクス分野である．量子ホール系やトポロジカル絶縁体に代表されるトポロジカル物質は，その性質の理解にトポロジー（位相幾何学）と呼ばれる数学分野の考え方を応用することから，この名が付けられている．

　トポロジーとは，対象の形状を「切ったり貼ったりしない」連続変形において不変な性質を扱う数学分野である．図1（a）のように，ボールとドーナツはそれぞれ穴の数が0と1で異なるため，切り貼りせずに互いの形に変形できない．一方，ドーナツとカップは，どちらも穴が一つであり移り変わることができる．このように，トポロジーでは「穴の数」のように離散的な値をとる特徴量（トポロジカル不変量）によって対象を分類する．

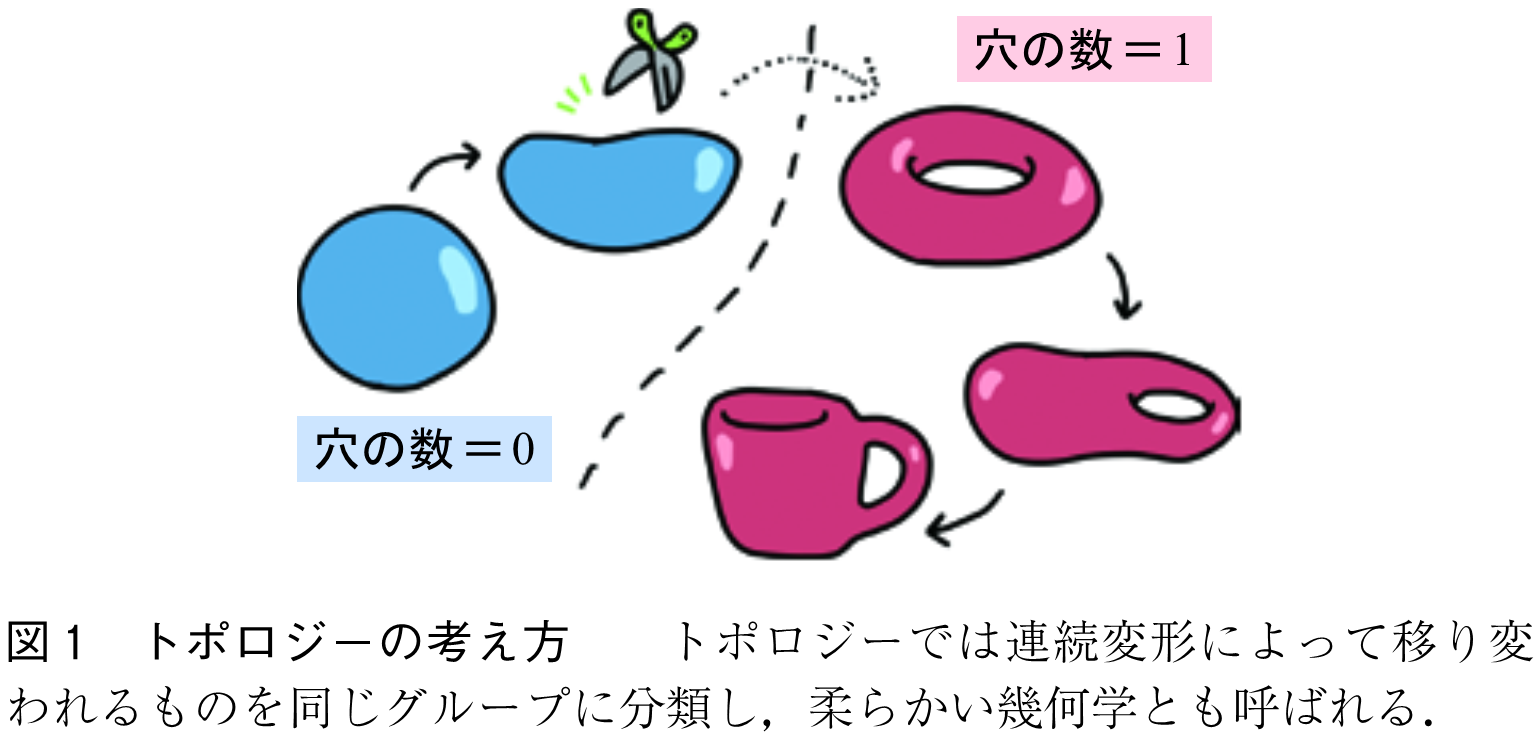
　トポロジカル物質では，バンド構造が持つトポロジカル不変量（バンドトポロジー）によって物質の性質を理解・予言できる．このバンドトポロジーのアイデアを，光系に適用したものが，光トポロジカル絶縁体・トポロジカルフォトニック結晶と呼ばれ，トポロジカルフォトニクスにおける中心的な研究対象となっている^(1),(2)．

　トポロジカルフォトニクスは，2008年のHaldaneとRaghuによる光版の量子ホール系の提案^(3),(4)に端を発し，磁界を印加した系での実験⁽⁵⁾が報告された．その後，誘電体構造のみで実現可能な系が提案されると^(6),(7)，既存の半導体作製技術で実現可能であったことから，研究開発が一気に加速し，トポロジカルフォトニクス分野の広がりにつながった．

　トポロジカルフォトニクスが大きな注目を集めた理由の一つは，「光トポロジカルエッジ状態」を用いた光導波路にある．この光導波は，円偏光のカイラリティと伝搬方向がロックした一方向性伝搬や，急峻な曲げや欠陥に対する耐性を示すことが報告され，光回路への応用や新しい原理の光技術への期待から大きな注目を集めた．

2．トポロジカル絶縁体とバンドトポロジー

　トポロジカル絶縁体（Topological Insulator，以降，TI）の最大の特徴はその電気伝導特性にある．絶縁体と金属は物質内部（バルク）と表面（エッジ）とで電気伝導特性が変わらないのに対して，TIは内部では絶縁体的に振る舞う一方表面では金属のように電気伝導が許される．この表面伝導は「トポロジカルエッジ状態」と呼ばれる表面状態が担っており，非磁性不純物に対して反射されないという欠陥耐性（トポロジカル保護）を持つ⁽⁸⁾．

　このようなTIの「バンドトポロジー」は，各バンドに付随する波動関数の「位相」によって決まる．あるバンド内において，波数空間内の経路を一周する際に，波動関数が獲得する位相（幾何学的位相）を「ベリー位相」と呼び，それをブリルアンゾーン全域で足し合わせ2πで割ったものが「チャーン数」と呼ばれるトポロジカル不変量である⁽⁸⁾．チャーン数は整数になることが知られており，直観的には「バンド内で位相が何回ねじれているか」を表す量である．通常の絶縁体では，チャーン数は常に0だが，TIでは0以外の値をとる．各バンドのチャーン数からギャップ中のトポロジカルエッジ状態の存在を予言することができ，これを「バルクエッジ対応」と呼ぶ⁽⁸⁾．非常に大雑把に言えば，バンド形状だけでなく，波動関数の質的な違いに着目することで新たな設計自由度が加わったのがTIである．

3．トポロジカルフォトニック結晶

　トポロジカルフォトニック結晶は，時間反転対称性のないもの（光版量子ホール系^(3),(4)）と時間反転対称性のあるもの（光版量子スピンホール系（光版TI)⁽⁶⁾，光版量子バレーホール系⁽⁷⁾）に大別される．以下では，半導体作製技術で実現可能な，時間反転対称性のある系について説明する．

　光版量子スピンホール系では，WuとHuによって提案された構造⁽⁶⁾(以下，WH型）が有名である．WH型では，図2（a）～（c）のようにハネカム格子の単位胞を3倍に拡張し，三角穴が6回回転対称に空いた構造を考える⁽⁹⁾．この構造に，三角穴を内外にずらすような摂動を加える．摂動がない場合，図2（b）のようにバンドはΓ点で縮退し，ギャップレスになる．ここに摂動を加えると，図2（a），（c）のようにΓ点でギャップが開く．穴が中心に集まる場合，トリビアル（自明，トポロジカル不変量は0）なバンドギャップになり，これは通常のフォトニック結晶と同様である．一方，穴が中心から離れる摂動の場合，トポロジカル（非自明，トポロジカル不変量は1）なバンドギャップが形成でき，トポロジカルフォトニック結晶となる．

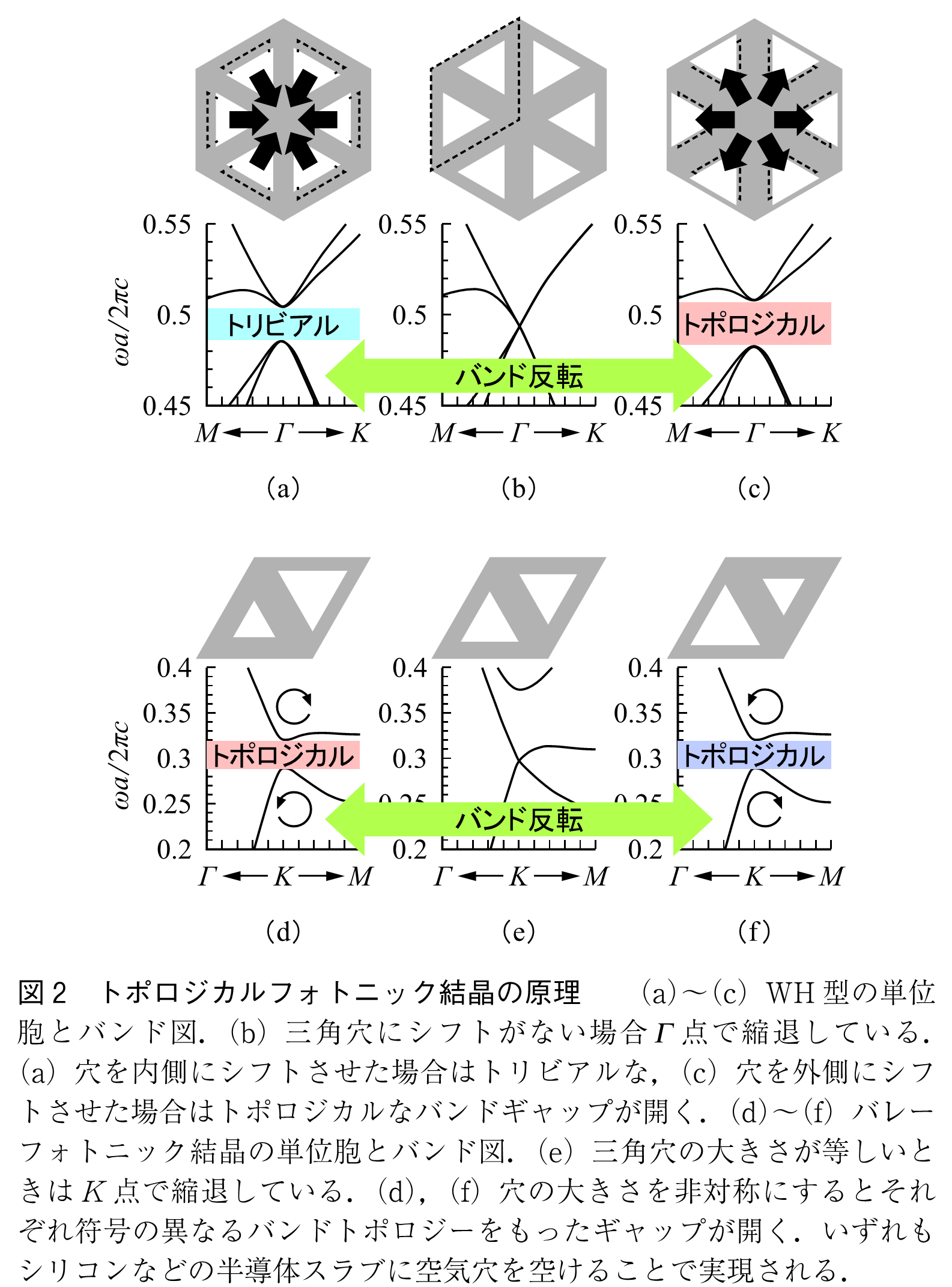
　光版量子バレーホール系は，バレーフォトニック結晶と呼ばれる．こちらでは，図2（d）～（f）のように，ハネカム格子の二つの穴の大きさを非対称にし，単位胞の反転対称性を破るような摂動を考える．二つの穴の大きさが等しいときは，点でディラック縮退があるが，一たび非対称になるとディラック縮退が解けギャップが出現する．このギャップの両端の電磁状態では，電磁界の位相が回転する渦が形成されており，その回転方向が互いに逆になっている．また構造の対称性から，この渦の向きは点とその反対の点とで互いに逆になる．この回転方向の自由度は，バレー自由度と呼ばれる．バレー自由度を持つ系では，反転対称性の破り方によって正負の符号の異なるバンドトポロジーを持つ．

　これら二つの系ではどちらも，ギャップの開閉の前後でバンドトポロジーが変化する．このギャップを閉じるという状況が，図1における「切り貼り」に対応しており，ギャップレス状態を介してバンドの相対関係が入れ替わることを「バンド反転」と呼ぶ．多くの場合，このバンド反転によって，バンドトポロジーを変化させることができる．

4．光トポロジカルエッジ状態

　量子ホール系及び量子スピンホール系では，バンドトポロジーによってエッジ状態が出現する．量子ホール系（図3（a））では，特定のスピンが一方向のみに伝導するカイラルエッジ状態が発現し，その光アナロジーとして，磁界を印加した光版量子ホール系では，光版のカイラルエッジ状態が発現する．この光エッジ状態は，欠陥などの障害に対してロバストな伝搬特性を示し，これは光版のトポロジカル保護に対応する^(3)～(5)．

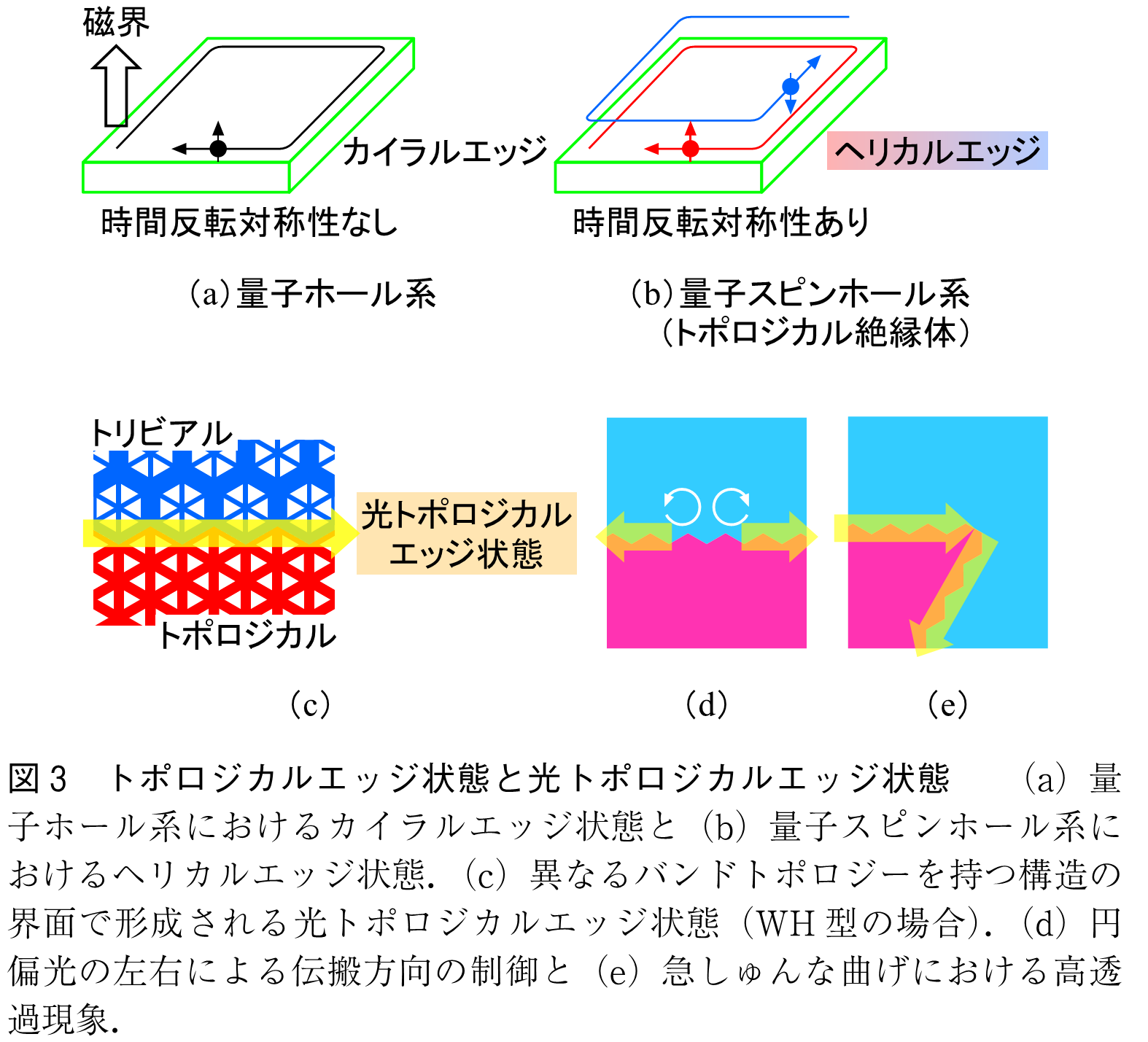
　一方，量子スピンホール系は，スピンと進行方向を反転させた二つの量子ホール系を重ねたようなものになっており，そのエッジ状態はヘリカルエッジ状態と呼ばれる⁽⁸⁾．TIの表面伝導を担うトポロジカルエッジ状態は，このヘリカルエッジ状態になっており，バンドトポロジーの異なる物質の界面において出現する．トポロジカルフォトニック結晶でも，図3（c）のように異なるバンドトポロジーを持つ構造の界面において，光版のトポロジカルエッジ状態を実現することができる．

　WH型やバレーフォトニック結晶による光トポロジカルエッジ状態は，一次元的な界面を導波する光導波路状態であり，以下のような特性を持つ．光エッジ状態は，バンドトポロジーによって有無が決定されるため，バンドトポロジーの変化によるスイッチングができる⁽¹⁰⁾．更に，励起円偏光の左右に対応して導波方向をスイッチできることや，急峻な曲げがあっても高い効率で導波することなどが報告されている⁽⁶⁾．これらの特性は，光回路における反射の抑制や小形化，光角運動量制御技術への応用が期待される．ただし，これらの光エッジ状態は，厳密な意味でのトポロジカル保護はないため，注意が必要である⁽¹¹⁾．WH型では光エッジ状態をスラブ面外からの光入射で直接励振できる．一方，バレーフォトニック結晶ではスラブ面外から励振できないが，放射損がないため長距離伝搬が必要な光回路応用に向いている．

5．おわりに

　トポロジカルフォトニクスは，従来のバンド構造のみに基づいた設計手法に，電磁状態のトポロジーという新たな自由度を導入することで，ナノフォトニクスに革新的な視点をもたらした．トポロジカルフォトニクスは，当初は主にトポロジカルフォトニック結晶を対象とする研究領域として始まったが，トポロジーという概念の一般性の高さから，現在ではより広範なナノフォトニクス分野をも含む大きな潮流となりつつあり，更に多様な広がりが期待される．

文　　　　　献

（2025年4月15日受付　2025年5月27日最終受付）